MECÁNICA CUÁNTICA

El teorema de Bell es un " teorema de no usar " que hace una distinción importante entre la mecánica cuántica y el mundo, tal como lo describe la mecánica clásica , particularmente en relación con el enredo cuánticodonde dos o más partículas en un estado cuántico continúan siendo mutuamente dependientes, incluso en general físicas. separaciones Este teorema lleva el nombre de John Stewart Bell .

Una serie de experimentos ha verificado el teorema y ha demostrado que el entrelazamiento cuántico se produce en grandes distancias. El entrelazamiento cuántico tiene profundas implicaciones para los resultados de las mediciones de los sistemas cuánticos; Por ejemplo, en computación cuántica .

En su forma más simple, el teorema de Bell afirma: ^[1]

Ninguna teoría física de las variables locales ocultas puede reproducir todas las predicciones de la mecánica cuántica.

El físico de estado sólido de Cornell , David Mermin, describió las valoraciones de la importancia del teorema de Bell en la comunidad física, que van desde la "indiferencia" a la "extravagancia salvaje". ^[2] Elfísico de partículas de Lawrence Berkeley Henry Stapp declaró: "El teorema de Bell es el descubrimiento más profundo de la ciencia". ^[3]

El teorema de Bell descarta las variables locales ocultas como una explicación viable de la mecánica cuántica (aunque todavía deja la puerta abierta a las variables ocultas no locales, como la teoría de De Broglie-Bohm , etc.). Bell concluyó:

En una teoría en la que los parámetros se agregan a la mecánica cuántica para determinar los resultados de mediciones individuales, sin cambiar las predicciones estadísticas, debe haber un mecanismo por el cual el ajuste de un dispositivo de medición puede influir en la lectura de otro instrumento, aunque sea remoto. Además, la señal involucrada debe propagarse instantáneamente, de modo que tal teoría no pueda ser invariante de Lorentz . ^[4]

Bell resumió una de las posibles formas de abordar el teorema, el superdeterminismo , en una entrevista de Radio BBC de 1985:

Hay una manera de escapar de la inferencia de las velocidades superluminales y la acción fantasmal a distancia. Pero implica un determinismo absoluto en el universo, la ausencia total de libre albedrío . Supongamos que el mundo es súper determinista, ya que no solo la naturaleza inanimada funciona en un reloj detrás de escena, sino nuestro comportamiento, incluida nuestra creencia de que somos libres de elegir hacer un experimento en lugar de otro, absolutamente predeterminado, incluido el La decisión del experimentador de realizar un conjunto de mediciones en lugar de otro, la dificultad desaparece. No hay necesidad de una señal más rápida que la luz para indicar a la partícula A qué medición se ha realizado en la partícula  B, porque el universo, incluida la partícula  A , ya "sabe" cuál será esa medida y su resultado.

Ejemplo de simple desigualdad de tipo Bell y su violación en la mecánica cuántica. Arriba: asumiendo cualquier distribución de probabilidad entre 8 posibilidades para valores de 3 variables binarias ABC, siempre obtenemos la desigualdad anterior. Abajo: ejemplo de su violación usando la reglacuántica de Nacimiento : la probabilidad es un cuadrado de amplitud normalizado.

Antecedentes históricos [ editar ]

A principios de la década de 1930, las implicaciones filosóficas de las interpretaciones actuales de la teoría cuántica preocuparon a muchos físicos prominentes de la época, incluido Albert Einstein . En un conocido artículo de 1935, Boris Podolsky y sus coautores Einstein y Nathan Rosen (colectivamente "EPR") intentaron demostrar mediante la paradoja de EPR que la mecánica cuántica estaba incompleta. Esto proporcionó la esperanza de que algún día se descubriera una teoría más completa (y menos preocupante). Pero esa conclusión se basó en los supuestos aparentemente razonables de localidad y realismo (juntos llamados "realismo local" o " variables locales ocultas").", a menudo indistintamente). En la lengua vernácula de Einstein: la localidad no significaba una acción instantánea (" espeluznante ") a distancia ; el realismo significaba que la luna estaba allí incluso cuando no se observaba. Estas suposiciones se debatieron acaloradamente en la comunidad física, especialmente entre Einstein y Niels Bohr .

En su innovador artículo de 1964, "Sobre la paradoja de Einstein Podolsky Rosen", ^{[4] [6] el} físico John Stewart Bell presentó una analogía (basada en mediciones de espín en pares de electrones enredados) a la paradoja hipotética de EPR. Utilizando su razonamiento, dijo, una elección de configuración de medición aquí no debería afectar el resultado de una medición allí (y viceversa). Después de proporcionar una formulación matemática de la localidad y el realismo basado en esto, mostró casos específicos en los que esto sería inconsistente con las predicciones de la teoría de la mecánica cuántica.

En pruebas experimentales siguiendo el ejemplo de Bell, ahora se utiliza el entrelazamiento cuántico de fotones en lugar de electrones, John Clauser y Stuart Freedman (1972) y Alain Aspect et al . (1981) demostraron que las predicciones de la mecánica cuántica son correctas a este respecto, aunque se basan en suposiciones no verificables adicionales que abren brechas para el realismo local.

En octubre de 2015, Hensen y sus colaboradores ^[7] informaron que realizaron una prueba de Bell sin fallas que podría obligar a uno a rechazar al menos uno de los principios de localidad, realismo o libertad de elección (el último "podría" " Conducir a teorías superdeterministas alternativas ). ^[8]Dos de estas posibilidades lógicas, la no localidad y el no realismo, corresponden a interpretaciones bien desarrolladas de la mecánica cuántica y tienen muchos partidarios; Este no es el caso para la tercera posibilidad lógica, la no libertad. La evidencia experimental concluyente de la violación de la desigualdad de Bell reduciría drásticamente la clase de teorías deterministas aceptables, pero no falsificaría el determinismo absoluto, que fue descrito por el mismo Bell como "no solo una naturaleza inanimada que funciona en un reloj detrás de escena, sino con nuestro comportamiento" , incluida nuestra creencia de que somos libres de elegir hacer un experimento en lugar de otro, absolutamente predeterminado ". Sin embargo, el propio Bell consideraba el determinismo absoluto como una solución inverosímil.

Descripción general [ editar ]

El teorema de Bell afirma que cualquier teoría física que incorpore el realismo local no puede reproducir todas las predicciones de la teoría de la mecánica cuántica. Debido a que numerosos experimentos están de acuerdo con las predicciones de la teoría de la mecánica cuántica y muestran diferencias entre las correlaciones que no pueden explicarse por las variables locales ocultas, muchos han considerado que los resultados experimentales refutan el concepto de realismo local como una explicación de los fenómenos físicos en que se basan. prueba. Para una teoría de variables ocultas, si las condiciones de Bell son correctas, los resultados que concuerdan con la teoría de la mecánica cuántica parecen indicar efectos superluminales (más rápidos que la luz), en contradicción con el principio de localidad.

Estos tres conceptos clave (localidad, realismo, libertad) son altamente técnicos y muy debatidos. En particular, el concepto de realismo ahora es algo diferente de lo que era en las discusiones en los años treinta. Es más precisamente llamado definición contrafactual ; significa que podemos pensar que los resultados de mediciones que en realidad no se realizaron son tan parte de la realidad como las que se hicieron. La localidad es la abreviatura de la causalidad relativista local . (Las teorías de campos cuánticos actualmente aceptadas sonlocales en la terminología del formalismo de Lagrangian y el enfoque axiomático ). Libertad se refiere a la posibilidad física de determinar la configuración de los dispositivos de medición independientemente del estado interno del sistema físico que se está midiendo.

Ilustración de la prueba de Bell para partículas de medio giro como los electrones. Una fuente produce un par singlete , una partícula se envía a una ubicación y la otra se envía a otra ubicación. Una medición de la propiedad enredada se realiza en varios ángulos en cada ubicación. El esquema para las mediciones en fotones es muy similar: el estado cuántico es diferente pero tiene propiedades muy similares.

El teorema generalmente se prueba considerando un sistema cuántico de dos qubits enredados . Los ejemplos más comunes se refieren a sistemas de partículas que se enredan en el giro o la polarización . La mecánica cuántica permite predicciones de correlaciones que se observarían si estas dos partículas tuvieran su giro o polarización medidos en diferentes direcciones. Bell demostró que si se mantiene una teoría local de variables ocultas, entonces estas correlaciones tendrían que satisfacer ciertas restricciones, llamadas desigualdades de Bell. Sin embargo, para las correlaciones cuánticas que surgen en el ejemplo específico considerado, esas restricciones no se satisfacen, por lo tanto, el fenómeno que se está estudiando no puede explicarse por una teoría local de variables ocultas.

Siguiendo el argumento del papel de la paradoja de Einstein – Podolsky – Rosen (EPR) (pero usando el ejemplo del giro, como en la versión de David Bohm del argumento EPR ^[4] [9] ), Bell consideró un experimento en el que hay "un par de partículas de medio giro se formaron de alguna manera en el estado de giro único y se movían libremente en direcciones opuestas". ^[4] Las dos partículas se alejan una de la otra a dos ubicaciones distantes, en las que se realizan mediciones de espín, a lo largo de ejes que se eligen de forma independiente. Cada medición arroja un resultado de giro (+) o giro (-); es decir, girar en la dirección positiva o negativa del eje elegido.

La probabilidad de que se obtenga el mismo resultado en las dos ubicaciones depende de los ángulos relativos en los que se realizan las dos mediciones de espín, y es estrictamente entre cero y uno para todos los ángulos relativos que no sean alineaciones perfectamente paralelas o antiparalelas (0 ° o 180 ° ). Dado que el momento angular total se conserva, y como el giro total es cero en el estado de singlete, la probabilidad del mismo resultado con alineación paralela (antiparalela) es 0 (1). Esta última predicción es tanto clásica como cuántica mecánicamente.

El teorema de Bell se refiere a las correlaciones definidas en términos de promedios tomados en muchos ensayos del experimento. La correlación de dos variables binarias se define generalmente en la física cuántica como el promedio de los productos de los pares de mediciones. Tenga en cuenta que esto es diferente de la definición habitual de correlación en las estadísticas. "Correlación" del físico cuántico es "(, unnormalized uncentered) en bruto de productos de la estadística momento". Son similares en cuanto a que, con cualquier definición, si los pares de resultados son siempre los mismos, la correlación es +1; si los pares de resultados son siempre opuestos, la correlación es -1; y si los pares de resultados concuerdan El 50% del tiempo, entonces la correlación es 0. La correlación se relaciona de manera simple con la probabilidad de resultados iguales, es decir, es igual al doble de la probabilidad de resultados iguales, menos uno.

Al medir el giro de estas partículas enredadas en direcciones anti-paralelas, es decir, a lo largo del mismo eje pero en direcciones opuestas, el conjunto de todos los resultados está perfectamente correlacionado. Por otro lado, si las mediciones se realizan en direcciones paralelas, siempre producen resultados opuestos, y el conjunto de mediciones muestra una perfecta anti-correlación. Esto está de acuerdo con las probabilidades indicadas anteriormente de medir el mismo resultado en estos dos casos. Finalmente, la medición en direcciones perpendiculares tiene un 50% de probabilidad de concordancia, y el conjunto total de mediciones no está correlacionado. Estos casos básicos se ilustran en la siguiente tabla. Las columnas deben leerse como ejemplosde pares de valores que Alice y Bob podrían registrar a medida que aumenta el tiempo yendo hacia la derecha.

Anti-paralelo	Par
	1	2	3	4	...	norte
Alicia , 0 °	+	-	+	+	...	-
Bob , 180 °	+	-	+	+	...	-
Correlación	(+1	+1	+1	+1	...	+1)	/ n = +1
							(100% idéntico)
Paralela	1	2	3	4	...	norte
Alicia , 0 °	+	-	-	+	...	+
Bob , 0 ° o 360 °	-	+	+	-	...	-
Correlación	(−1	−1	−1	−1	...	−1)	/ n = −1
							(100% opuesto)
Ortogonal	1	2	3	4	...	norte
Alicia, 0 °	+	-	+	-	...	-
Bob, 90 ° o 270 °	-	-	+	+	...	-
Correlación	(−1	+1	+1	−1	...	+1)	/ n = 0
							(50% idéntico, 50% opuesto)

La mejor imitación realista local posible (rojo) para la correlación cuántica de dos giros en el estado de singlete (azul), insistiendo en una perfecta anti-correlación a 0 °, una correlación perfecta en 180 °. Existen muchas otras posibilidades para la correlación clásica sujeta a estas condiciones laterales, pero todas se caracterizan por picos (y valles) agudos a 0 °, 180 ° y 360 °, y ninguna tiene valores más extremos (± 0.5) a 45 °, 135 °, 225 ° y 315 °. Estos valores están marcados con estrellas en el gráfico, y son los valores medidos en un experimento estándar de tipo Bell-CHSH: QM permite ± 1 / √ 2 = ± 0.7071… , el realismo local predice ± 0.5 o menos.

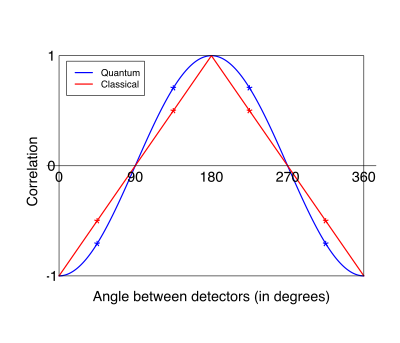
Con las medidas orientadas en ángulos intermedios entre estos casos básicos, la existencia de variables locales ocultas podría coincidir con / sería coherente con una dependencia lineal de la correlación en el ángulo pero, según la desigualdad de Bell (ver a continuación), no podría estar de acuerdo con la dependencia predicha por la teoría de la mecánica cuántica, es decir, que la correlación es el coseno negativo del ángulo. Los resultados experimentales coinciden con la curva predicha por la mecánica cuántica. ^[1]

A lo largo de los años, el teorema de Bell ha sido sometido a una gran variedad de pruebas experimentales. Sin embargo, se han identificado varias deficiencias comunes en la prueba del teorema , incluida la laguna de detección ^[10] y la laguna de comunicación . ^[10] A lo largo de los años, los experimentos se han mejorado gradualmente para abordar mejor estas lagunas. En 2015, se realizó el primer experimento para abordar simultáneamente todas las lagunas. ^[7]

Hasta la fecha, el teorema de Bell generalmente se considera respaldado por un corpus sustancial de evidencia y hay pocos partidarios de las variables ocultas locales, aunque el teorema es continuamente objeto de estudio, crítica y refinamiento. ^[11] [12]

Importancia [ editar ]

El teorema de Bell, derivado de su artículo seminal de 1964 titulado Sobre la paradoja de Einstein Podolsky Rosen , ^[4] ha sido llamado, en el supuesto de que la teoría es correcta, "la más profunda de la ciencia". ^[13]Quizás de igual importancia es el esfuerzo deliberado de Bell para alentar y traer legitimidad para trabajar en los problemas de integridad, que habían caído en la mala reputación. ^[14] Más adelante en su vida, Bell expresó su esperanza de que ese trabajo "continúe inspirando a aquellos que sospechan que lo que se prueba con las pruebas de imposibilidad es la falta de imaginación". ^[14]

El título del artículo seminal de Bell se refiere al artículo de 1935 de Einstein, Podolsky y Rosen ^[15] que desafió la integridad de la mecánica cuántica. En su artículo, Bell partió de los mismos dos supuestos que hizo el EPR, a saber (i) la realidad (que los objetos microscópicos tienen propiedades reales que determinan los resultados de las mediciones de la mecánica cuántica) y (ii) la localidad (que la realidad en una ubicación no se ve afectada). por mediciones realizadas simultáneamente en un lugar distante). Bell pudo derivar de estos dos supuestos un resultado importante, a saber, la desigualdad de Bell. La violación teórica (y posteriormente experimental) de esta desigualdad implica que al menos uno de los dos supuestos debe ser falso.

En dos aspectos, el documento de Bell de 1964 fue un paso adelante en comparación con el documento de EPR: en primer lugar, consideraba más variables ocultas que simplemente el elemento de la realidad física en el documento de EPR; y la desigualdad de Bell era, en parte, experimentalmente comprobable, lo que plantea la posibilidad de probar la hipótesis del realismo local. Las limitaciones en tales pruebas hasta la fecha se detallan a continuación. Mientras que el artículo de Bell trata solo con teorías de variables ocultas deterministas, el teorema de Bell también se generalizó a las teorías estocásticas ^[16] , y también se realizó ^[17]el teorema no se trata tanto de variables ocultas, sino de los resultados de las mediciones que podrían haberse tomado en lugar de las que realmente se tomaron. La existencia de estas variables se denomina suposición de realismo, o suposición de definición contrafactual .

Después del documento de EPR, la mecánica cuántica estaba en una posición insatisfactoria: o estaba incompleta, en el sentido de que no daba cuenta de algunos elementos de la realidad física, o violaba el principio de una velocidad de propagación finita de los efectos físicos. En una versión modificada del experimento mental EPR, dos observadores hipotéticos , ahora conocidos comúnmente como Alice y Bob , realizan mediciones independientes del giro en un par de electrones, preparados en una fuente en un estado especial llamado estado singlete del giro . Es la conclusión del EPR que una vez que Alice mide el giro en una dirección (por ejemplo, en la xeje), la medida de Bob en esa dirección se determina con certeza, ya que es el resultado opuesto al de Alicia, mientras que inmediatamente antes de la medición de Alicia, el resultado de Bob solo se determinó estadísticamente (es decir, era solo una probabilidad, no una certeza); por lo tanto, o el giro en cada dirección es un elemento de la realidad física , o los efectos viajan de Alicia a Bob al instante.

En QM, las predicciones se formulan en términos de probabilidades , por ejemplo, la probabilidad de que un electrón se detecte en un lugar en particular, o la probabilidad de que su giro esté hacia arriba o hacia abajo. Sin embargo, la idea persistió en que el electrón de hecho tiene una posición y un giro definidos , y que la debilidad de QM es su incapacidad para predecir esos valores con precisión. Existía la posibilidad de que alguna teoría desconocida, como la teoría de las variables ocultas , pudiera predecir esas cantidades exactamente, mientras que al mismo tiempo también estuviera completamente de acuerdo con las probabilidades predichas por QM. Si existe tal teoría de variables ocultas, entonces, debido a que QM no describe las variables ocultas, esta última sería una teoría incompleta.

Realismo local [ editar ]

El concepto de realismo local se formaliza para establecer y probar el teorema y las generalizaciones de Bell. Un enfoque común es el siguiente:

1. Existe un espacio de probabilidad Λ y los resultados observados por Alice y Bob resultan por muestreo aleatorio del parámetro (desconocido, "oculto") λ ∈ Λ .
2. Los valores observados por Alice o Bob son funciones de la configuración del detector local y solo del parámetro oculto. Por lo tanto, hay funciones A , B  : S ² × Λ → {-1, +1} , donde un ajuste del detector se modela como una ubicación en la esfera de la unidad S ² , de manera que
   • El valor observado por Alicia con el detector a es A ( a , λ )
   • El valor observado por Bob con el ajuste del detector b es B ( b , λ )

La anti-correlación perfecta requeriría B ( c , λ ) = - A ( c , λ ), c ∈ S ² . Implícito en el supuesto 1) anterior, el espacio del parámetro oculto Λ tiene una medida de probabilidad μ y se escribe la expectativa de una variable aleatoria X en Λ con respecto a μ

$${\ displaystyle \ operatorname {E} (X) = \ int _ {\ Lambda} X (\ lambda) p (\ lambda) d \ lambda,}

donde para la accesibilidad de la notación, asumimos que la medida de probabilidad tiene una densidad de probabilidad p que, por lo tanto, no es negativa y se integra a 1 . A menudo se piensa que el parámetro oculto está asociado con la fuente, pero también puede contener componentes asociados con los dos dispositivos de medición.

Desigualdades de Bell [ editar ]

Las desigualdades de campanas se refieren a mediciones hechas por observadores en pares de partículas que han interactuado y luego se separaron. Suponiendo un realismo local, ciertas restricciones deben mantenerse en las relaciones entre las correlaciones entre las mediciones subsiguientes de las partículas bajo diversos ajustes de medición posibles. Sean A y B como se indica arriba. Definir para los presentes propósitos tres funciones de correlación:

• Sea C _e ( a , b ) la correlación medida experimentalmente definida por

  $${\ displaystyle C_ {e} (a, b) = {\ frac {N _ {++} + N _ {-} - N _ {+ -} - N _ {- +}} {N _ {++} + N_ { -} + N _ {+ -} + N _ {- +}}},}

donde N ₊₊ es el número de mediciones que producen "spin up" en la dirección de a medida por Alice (primer subíndice + ) y "spin up" en la dirección de b medida por Bob. Las otras apariciones de N se definen de manera análoga.

• Dejemos que C _q ( a , b ) denote la correlación según lo predicho por la mecánica cuántica. Esto está dado por la expresión

  $${\ displaystyle C_ {q} (a, b) = \ left \ langle A \ left | ({\ boldsymbol {\ sigma}} \ cdot \ mathbf {b}) ^ {(2)} ({\ boldsymbol {\ sigma}} \ cdot \ mathbf {a}) ^ {(1)} \ right | A \ right \ rangle,}

donde A es la función de onda de espín antisimétrica. Este valor se calcula para ser

$${\ displaystyle C_ {q} (a, b) = - \ mathbf {a} \ cdot \ mathbf {b}.}

• Dejemos que C _h ( a , b ) denote la correlación como predice cualquier teoría de variables ocultas. En la formalización de arriba, esto es

  $${\ displaystyle C_ {h} (a, b) = E (A (\ mathbf {a}, \ lambda) B (\ mathbf {b}, \ lambda)) = \ int _ {\ Lambda} A (\ mathbf {a}, \ lambda) B (\ mathbf {b}, \ lambda) p (\ lambda) d \ lambda.}

espectáculo

Detalles sobre el cálculo de C _q ( a , b )

Con esta notación, se puede hacer un resumen conciso de lo que sigue.

• Teóricamente, existe a , b tal que

$${\ displaystyle C_ {q} \ neq C_ {h},}

cualesquiera que sean las características particulares de la teoría de la variable oculta, siempre y cuando se atenga a las reglas del realismo local como se definió anteriormente. Es decir, ninguna teoría local de variables ocultas puede hacer las mismas predicciones que la mecánica cuántica.

• Experimentalmente, instancias de

$${\ displaystyle C_ {e} \ neq C_ {h}}

Se han encontrado (cualquiera que sea la teoría de la variable oculta), pero

$${\ displaystyle C_ {e} \ neq C_ {q} \ quad {\ text {(no encontrado)}}}

nunca ha sido encontrado. Es decir, las predicciones de la mecánica cuántica nunca han sido falsificadas por el experimento. Estos experimentos incluyen aquellos que pueden descartar teorías locales de variables ocultas. Pero ver más abajo sobre posibles lagunas.

La desigualdad de Bell original [ editar ]

La desigualdad que Bell derivó se puede escribir como: ^[4]

$${\ displaystyle C_ {h} (a, c) -C_ {h} (b, a) -C_ {h} (b, c) \ leq 1,}

donde a, b y c se refieren a tres configuraciones arbitrarias de los dos analizadores. Sin embargo, esta desigualdad está restringida en su aplicación al caso bastante especial en el que los resultados en ambos lados del experimento siempre son exactamente anticorrelacionados cuando los analizadores son paralelos. La ventaja de restringir la atención a este caso especial es la simplicidad resultante de la derivación. En el trabajo experimental, la desigualdad no es muy útil porque es difícil, si no imposible, crear una anti-correlación perfecta .

Sin embargo, esta forma simple tiene una explicación intuitiva. Es equivalente al siguiente resultado elemental de la teoría de la probabilidad. Considere tres ( X, Y y Z ) de tirones de moneda (altamente correlacionados y posiblemente sesgados) con la propiedad de:

1. X e Y dan el mismo resultado (ambas cabezas o ambas colas) el 99% del tiempo
2. Y y Z también dan el mismo resultado el 99% del tiempo,

entonces X y Z también deben producir el mismo resultado al menos el 98% del tiempo. El número de desajustes entre X e Y (1/100) más el número de desajustes entre Y y Z (1/100) son juntos el número máximo posible de desajustes entre X y Z (una simple desigualdad Boole-Fréchet ).

Imagina un par de partículas que se pueden medir en lugares distantes. Supongamos que los dispositivos de medición tienen configuraciones, que son ángulos, por ejemplo, los dispositivos miden algo llamado giro en alguna dirección. El experimentador elige las direcciones, una para cada partícula, por separado. Supongamos que el resultado de la medición es binario (p. Ej., Giro hacia arriba, giro hacia abajo). Supongamos que las dos partículas están perfectamente anti-correlacionadas, en el sentido de que cuando ambas se miden en la misma dirección, se obtienen resultados idénticamente opuestos, cuando ambas se miden en direcciones opuestas, siempre dan el mismo resultado. La única forma de imaginar cómo funciona esto es que ambas partículas abandonen su fuente común con, de alguna manera, los resultados que entregarán cuando se midan en cualquier dirección posible. (¿De qué otra manera podría la partícula 1 saber cómo dar la misma respuesta que la partícula 2 cuando se mide en la misma dirección? No saben de antemano cómo se van a medir ...). Puede pensarse que la medición en la partícula 2 (después de cambiar su signo) nos dice qué habría dado la misma medición en la partícula 1.

Comience con una configuración exactamente opuesta a la otra. Todos los pares de partículas dan el mismo resultado (cada par es un giro hacia arriba o ambos hacia abajo). Ahora cambia la configuración de Alice en un grado en relación con la de Bob. Ahora están un grado fuera de ser exactamente opuestos entre sí. Una pequeña fracción de los pares, digamos f , ahora da resultados diferentes. Si, por el contrario, habíamos dejado la configuración de Alice sin cambiar pero cambiamos la de Bob en un grado (en la dirección opuesta), entonces nuevamente una fracción de fDe los pares de partículas resulta dar resultados diferentes. Finalmente, considere lo que sucede cuando ambos turnos se implementan al mismo tiempo: las dos configuraciones ahora están exactamente a dos grados de distancia entre ellas. Según el argumento de la falta de coincidencia, la posibilidad de una falta de coincidencia en dos grados no puede ser más del doble de la posibilidad de una falta de coincidencia en un grado: no puede ser más de 2 f .

Compare esto con las predicciones de la mecánica cuántica para el estado de singlete. Para un ángulo pequeño θ , medido en radianes, la probabilidad de un resultado diferente es aproximadamente$${\ displaystyle f_ {1} = \ theta ^ {2} / 4}como se explica por la aproximación de ángulo pequeño . En dos veces este pequeño ángulo, la posibilidad de una falta de coincidencia es, por lo tanto, aproximadamente 4 veces mayor, ya que$${\ displaystyle f_ {2} = (2 \ theta) ^ {2} / 4 = 2 ^ {2} \ theta ^ {2} / 4 \ approx 4f_ {1}}. Pero solo argumentamos que no puede ser más de 2 veces más grande.

Esta formulación intuitiva se debe a David Mermin . El límite de ángulo pequeño se discute en el artículo original de Bell y, por lo tanto, se remonta al origen de las desigualdades de Bell.

Desigualdad CHSH [ editar ]

Artículo principal: desigualdad CHSH

Generalizando la desigualdad original de Bell, ^[4] John Clauser , Michael Horne, Abner Shimony y RA Holt introdujeron la desigualdad CHSH , ^[18] que pone límites clásicos en el conjunto de cuatro correlaciones en el experimento de Alicia y Bob, sin ninguna suposición de correlaciones perfectas ( o anti-correlaciones) en ajustes iguales

$${\ displaystyle (1) \ quad C_ {h} (a, b) + C_ {h} (a, b ') + C_ {h} (a', b) -C_ {h} (a ', b' ) \ leq 2.}

Haciendo la elección especial $${\ displaystyle a '= b + \ pi}, denotando $${\ displaystyle b '= c}, y asumiendo una perfecta anti-correlación en configuraciones iguales, correlación perfecta en configuraciones opuestas, por lo tanto $${\ displaystyle \ rho (a, a + \ pi) = 1} y $${\ displaystyle \ rho (b, a + \ pi) = - \ rho (b, a)}, la desigualdad CHSH se reduce a la desigualdad original de Bell. Hoy en día, (1) a menudo también se le llama simplemente "la desigualdad de Bell", pero a veces más completamente "la desigualdad de Bell-CHSH".

Derivación de la encuadernación clásica [ editar ]

Con notación abreviada.

$${\ displaystyle A = A (a, \ lambda), A '= A (a', \ lambda), B = B (b, \ lambda), B '= B (b', \ lambda),}

La desigualdad CHSH se puede derivar de la siguiente manera. Cada una de las cuatro cantidades es$${\ displaystyle \ pm 1} y cada uno depende de $${\ displaystyle \ lambda}. De ello se deduce que para cualquier$${\ displaystyle \ lambda \ in \ Lambda}, uno de $${\ displaystyle B + B '} y $${\ displaystyle B-B '} es cero, y el otro es $${\ displaystyle \ pm 2}. De esto se deduce que

$${\ displaystyle AB + AB '+ A'B-A'B' = A \ left (B + B '\ right) + A' \ left (B-B '\ right) \ leq 2,}

y por lo tanto

{\ displaystyle {\ begin {alineado} C_ {h} (a, b) + C_ {h} \ left (a, b '\ right) + C_ {h} \ left (a', b \ right) -C_ {h} \ left (a ', b' \ right) & = \ int _ {\ Lambda} ABpd \ lambda + \ int _ {\ Lambda} AB'pd \ lambda + \ int _ {\ Lambda} A'Bpd \ lambda - \ int _ {\ Lambda} A'B'pd \ lambda \\ & = \ int _ {\ Lambda} \ left (AB + AB '+ A'B-A'B' \ right) pd \ lambda \\ & = \ int _ {\ Lambda} \ left (A \ left (B + B '\ right) + A' \ left (B-B '\ right) \ right) pd \ lambda \ leq 2. \ end {alineado}}}

En el corazón de esta derivación se encuentra una simple desigualdad algebraica relativa a cuatro variables, $${\ displaystyle A, A ', B, B'}, que toman los valores $${\ displaystyle \ pm 1} solamente:

$${\ displaystyle AB + AB '+ A'B-A'B' = A \ left (B + B '\ right) + A' \ left (B-B '\ right) \ leq 2.}

Se considera que la desigualdad de CHSH depende solo de las siguientes tres características clave de la teoría de las variables ocultas locales: (1) realismo: junto con los resultados de las mediciones realmente realizadas, los resultados de las mediciones potencialmente realizadas también existen al mismo tiempo; (2) localidad, los resultados de las mediciones en la partícula de Alicia no dependen de la medición que Bob elija realizar en la otra partícula; (3) libertad: Alicia y Bob pueden elegir libremente qué medidas realizar.

El supuesto de realismo es en realidad un tanto idealista, y el teorema de Bell solo prueba la no localidad con respecto a las variables que solo existen por razones metafísicas ^{[ cita requerida ]} . Sin embargo, antes del descubrimiento de la mecánica cuántica, tanto el realismo como la localidad eran rasgos completamente no controvertidos de las teorías físicas.

Las predicciones mecánicas cuánticas violan las desigualdades de CHSH [ editar ]

Las mediciones realizadas por Alice y Bob son mediciones de espín en electrones. Alice puede elegir entre dos configuraciones de detector etiquetadas$${\ displaystyle a} y $${\ displaystyle a '}; estos ajustes corresponden a la medida de giro a lo largo del$${\ displaystyle z} o la $${\ displaystyle x}eje. Bob puede elegir entre dos configuraciones de detector etiquetadas$${\ displaystyle b} y $${\ displaystyle b '}; estos corresponden a la medida de giro a lo largo del$${\ displaystyle z '} o $${\ displaystyle x '} eje, donde el $${\ displaystyle x'-z '} sistema de coordenadas se gira 135 ° con respecto a la $${\ displaystyle xz}sistema coordinado. Los observables de espín están representados por las matrices autoadjuntadas 2 × 2:

{\ displaystyle S_ {x} = {\ begin {bmatrix} 0 & 1 \\ 1 & 0 \ end {bmatrix}}, \ quad S_ {z} = {\ begin {bmatrix} 1 & 0 \\ 0 & -1 \ end {bmatrix}} }

Estas son las matrices de spin de Pauli , que se sabe que tienen valores propios iguales a$${\ displaystyle \ pm 1}. Como es habitual, usaremos la notación bra-ket para denotar los vectores propios de$${\ displaystyle S_ {z}} como $${\ displaystyle | 0 \ rangle, | 1 \ rangle}, dónde

$$$${\ displaystyle | 0 \ rangle \ equiv {\ begin {pmatrix} 1 \\ 0 \ end {pmatrix}}, \ qquad | 1 \ rangle \ equiv {\ begin {pmatrix} 0 \\ 1 \ end {pmatrix}} .}

Considera ahora el estado único $${\ displaystyle | \ Phi ^ {-} \ rangle} definido como

$$$${\ displaystyle | \ Phi ^ {-} \ rangle \ equiv {\ frac {1} {\ sqrt {2}}} \ left (| 0,1 \ rangle - | 1,0 \ rangle \ right),}

donde usamos la notación reducida $${\ displaystyle | 0,1 \ rangle \ equiv | 0 \ rangle \ otimes | 1 \ rangle, | 1,0 \ rangle \ equiv | 1 \ rangle \ otimes | 0 \ rangle.}

De acuerdo con la mecánica cuántica, la elección de las mediciones se codifica en la elección de los operadores de Hermitian aplicados a este estado. En particular, consideremos los siguientes operadores:

{\ displaystyle {\ begin {alineado} A (a) & = S_ {z} \ otimes I \\ A (a ') & = S_ {x} \ otimes I \\ B (b) & = {\ frac { -1} {\ sqrt {2}}} \ I \ otimes (S_ {z} + S_ {x}) \\ B (b ') & = {\ frac {1} {\ sqrt {2}}} \ I \ otimes (S_ {z} -S_ {x}), \ end {alineado}}}

dónde $${\ displaystyle A (a), A (a ')} representan dos opciones de medición de Alicia, y $${\ displaystyle B (b), B (b ')} Dos opciones de medida de Bob.

Para obtener el valor de expectativa dado por una opción de medición dada de Alice y Bob, uno tiene que calcular el valor de expectativa del par de operadores correspondiente (por ejemplo, $${\ displaystyle A (a) B (b)} Si las entradas son elegidas para ser $${\ displaystyle a, b}) sobre el estado compartido $${\ displaystyle | \ Phi ^ {-} \ rangle}.

Por ejemplo, el valor de expectativa. $${\ displaystyle \ langle A (a) B (b) \ rangle} Corresponde a Alicia elegir la configuración de medición. $${\ displaystyle a} y Bob eligiendo la configuración de medición $${\ displaystyle b} se calcula como

$$$${\ displaystyle \ langle A (a) B (b) \ rangle \ equiv \ langle \ Phi ^ {-} | \ left ({\ frac {-1} {\ sqrt {2}}} S_ {z} \ otimes (S_ {x} + S_ {z}) \ right) | \ Phi ^ {-} \ rangle = - {\ frac {1} {2}} \ langle \ Phi ^ {-} | {\ Big [} | 0 \ rangle \ otimes (| 0 \ rangle - | 1 \ rangle) + | 1 \ rangle \ otimes (| 1 \ rangle + | 0 \ rangle) {\ Big]} = {\ frac {1} {\ sqrt { 2}}}.}

Se utilizan cálculos similares para obtener

{\ displaystyle {\ begin {alineado} \ left \ langle A (a) B (b) \ right \ rangle = \ left \ langle A \ left (a '\ right) B (b) \ right \ rangle = \ left \ langle A \ left (a '\ right) B \ left (b' \ right) \ right \ rangle & = {\ frac {1} {\ sqrt {2}}} \\\ left \ langle A (a) B \ left (b '\ right) \ right \ rangle & = - {\ frac {1} {\ sqrt {2}}}. \ End {alineado}}}

De ello se deduce que el valor de $${\ displaystyle S} dada por este arreglo experimental particular es

{\ displaystyle \ left \ langle A (a) B (b) \ right \ rangle + \ left \ langle A \ left (a '\ right) B \ left (b' \ right) \ right \ rangle + \ left \ langle A \ left (a '\ right) B (b) \ right \ rangle - \ left \ langle A (a) B \ left (b' \ right) \ right \ rangle = {\ frac {4} {\ sqrt {2}}} = 2 {\ sqrt {2}}> 2.}

Teorema de Bell: si el formalismo mecánico cuántico es correcto, entonces el sistema que consiste en un par de electrones entrelazados no puede satisfacer el principio del realismo local. Tenga en cuenta que$${\ displaystyle 2 {\ sqrt {2}}}es de hecho el límite superior para la mecánica cuántica llamado Tsirelson enlazado . Los operadores que dan este valor máximo son siempre isomorfos a las matrices de Pauli. ^[19]

Pruebas por experimentos prácticos [ editar ]

Esquema de una prueba de campana de "dos canales"
La fuente S produce pares de "fotones", enviados en direcciones opuestas. Cada fotón se encuentra con un polarizador de dos canales cuya orientación (aob) puede ser configurada por el experimentador. Las señales emergentes de cada canal se detectan y las coincidencias de cuatro tipos (++, −−, + - y - +) se cuentan por el monitor de coincidencia.

Artículo principal: experimentos de prueba de campana

Las pruebas experimentales pueden determinar si las desigualdades de Bell requeridas por el realismo local son compatibles con la evidencia empírica.

En realidad, la mayoría de los experimentos se han realizado utilizando polarización de fotones en lugar de espín de electrones (u otras partículas de medio giro). El estado cuántico del par de fotones entrelazados no es el estado singlete, y la correspondencia entre los ángulos y los resultados es diferente a la de la configuración de la mitad de giro. La polarización de un fotón se mide en un par de direcciones perpendiculares. En relación con una orientación dada, la polarización es vertical (denotada por V o por +) u horizontal (denotada por H o ​​por -). Los pares de fotones se generan en estado cuántico.

$${\ displaystyle {\ frac {1} {\ sqrt {2}}} \ left (| V \ rangle \ otimes | V \ rangle + | H \ rangle \ otimes | H \ rangle \ right)}

dónde $${\ displaystyle | V \ rangle} y $${\ displaystyle | H \ rangle}denota el estado de un solo fotón polarizado vertical u horizontalmente, respectivamente (relativo a una dirección de referencia fija y común para ambas partículas).

Cuando la polarización de ambos fotones se mide en la misma dirección, ambos dan el mismo resultado: correlación perfecta. Cuando se miden en direcciones que forman un ángulo de 45 ° entre sí, los resultados son completamente aleatorios (no correlacionados). Midiendo en direcciones a 90 ° entre sí, los dos están perfectamente anti-correlacionados. En general, cuando los polarizadores se encuentran en un ángulo θ entre sí, la correlación es cos (2 theta ) . Entonces, en relación con la función de correlación para el estado singlete de la mitad de las partículas de espín, tenemos una función de coseno positiva en lugar de negativa, y los ángulos se dividen en dos: la correlación es periódica con el período π en lugar de 2 π .

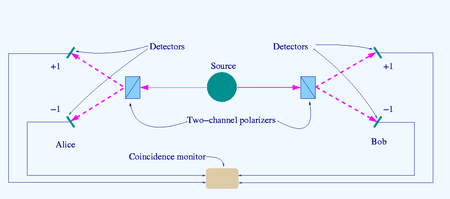
Las desigualdades de Bell se prueban mediante "recuentos de coincidencia" de un experimento de prueba de Bell como el que se muestra en el diagrama. Los pares de partículas se emiten como resultado de un proceso cuántico, se analizan con respecto a algunas propiedades clave, como la dirección de polarización, y luego se detectan. El experimentador selecciona el ajuste (orientaciones) de los analizadores.

Los experimentos de prueba de Bell hasta la fecha violan abrumadoramente la desigualdad de Bell.

Dos clases de desigualdades de Bell [ editar ]

El problema del muestreo justo se enfrentó abiertamente en la década de 1970. En los primeros diseños de su experimento de 1973, Freedman y Clauser ^[20] utilizaron un muestreo justo en la forma de la hipótesis de Clauser-Horne-Shimony-Holt (CHSH ^[18] ). Sin embargo, poco después Clauser y Horne ^[16] hizo la importante distinción entre desigualdades de Bell inhomogéneas (IBI) y homogéneas (HBI). La prueba de un IBI requiere que comparemos ciertas tasas de coincidencia en dos detectores separados con las tasas individuales de los dos detectores. Nadie necesitaba realizar el experimento, porque las tasas de individuales con todos los detectores en la década de 1970 eran al menos diez veces todas las tasas de coincidencia. Por lo tanto, teniendo en cuenta esta baja eficiencia del detector, la predicción de QM realmente satisfizo al IBI. Para llegar a un diseño experimental en el que la predicción de QM viola el IBI, necesitamos detectores cuya eficiencia supere el 82.8% para los estados singletes, ^[21] pero tienen una tasa de oscuridad muy baja y tiempos de resolución y muerte breves. Esto está ahora al alcance.

Desafíos prácticos [ editar ]

Artículo principal: Las lagunas en los experimentos de prueba de campana

Debido a que, en ese momento, incluso los mejores detectores no detectaron una gran fracción de todos los fotones, Clauser y Horne ^[16] reconocieron que probar la desigualdad de Bell requería algunas suposiciones adicionales. Introdujeron la Hipótesis de No Mejora (NEH):

Una señal de luz, que se origina en una cascada atómica, por ejemplo, tiene cierta probabilidad de activar un detector. Luego, si se interpone un polarizador entre la cascada y el detector, la probabilidad de detección no puede aumentar.

Dado este supuesto, existe una desigualdad de Bell entre las tasas de coincidencia con polarizadores y las tasas de coincidencia sin polarizadores.

El experimento fue realizado por Freedman y Clauser, ^[20] que descubrieron que se violaba la desigualdad de Bell. Por lo tanto, la hipótesis de no mejora no puede ser cierta en un modelo de variables ocultas locales.

Si bien los primeros experimentos utilizaron cascadas atómicas, los experimentos posteriores utilizaron conversión descendente paramétrica, siguiendo una sugerencia de Reid y Walls, ^{[22] que} proporcionaron propiedades mejoradas de generación y detección. Como resultado, los experimentos recientes con fotones ya no tienen que sufrir la laguna de detección. Esto convirtió al fotón en el primer sistema experimental para el cual se superaron todas las lagunas experimentales principales, aunque al principio solo en experimentos separados. A partir de 2015, los experimentadores pudieron superar todas las principales lagunas experimentales simultáneamente; Ver experimentos de prueba de campana .

Aspectos metafísicos [ editar ]

La mayoría de los defensores de la idea de las variables ocultas creen que los experimentos han descartado las variables locales ocultas. Están listos para abandonar la localidad, explicando la violación de la desigualdad de Bell mediante una teoría de variables ocultas no locales , en la que las partículas intercambian información sobre sus estados. Esta es la base de la interpretación de Bohm de la mecánica cuántica, que requiere que todas las partículas en el universo puedan intercambiar instantáneamente información con todas las demás. Un experimento de 2007 descartó una gran clase de teorías de variables ocultas no locales no de Bohmian. ^[23]

Si las variables ocultas pueden comunicarse entre sí más rápido que la luz, la desigualdad de Bell puede violarse fácilmente. Una vez que se mide una partícula, puede comunicar las correlaciones necesarias a la otra partícula. Como en la relatividad la noción de simultaneidad no es absoluta, esto no es atractivo. Una idea es reemplazar la comunicación instantánea con un proceso que viaja hacia atrás en el tiempo a lo largo del pasado cono de luz . Esta es la idea detrás de una interpretación transaccional de la mecánica cuántica, que interpreta el surgimiento estadístico de una historia cuántica como un acuerdo gradual entre las historias que avanzan y retroceden en el tiempo. ^[24]

Algunos defensores de los modelos deterministas no han renunciado a las variables locales ocultas. Por ejemplo, Gerard 't Hooft ha argumentado que la laguna del superdeterminismo no puede ser descartada. ^[25] [26]

La teoría de muchos mundos ofrece una solución posible (pero no aceptada universalmente)de la mecánica cuántica. De acuerdo con esto, no solo es ilusorio el colapso de la función de onda, sino que la aparente ramificación aleatoria de posibles futuros cuando los sistemas cuánticos interactúan con el mundo macroscópico también es una ilusión. La medición no conduce a una elección aleatoria del posible resultado; más bien, el único ingrediente de la mecánica cuántica es la evolución unitaria de la función de onda. Todas las posibilidades coexisten para siempre y la única realidad es la función de onda mecánica cuántica. Según este punto de vista, dos observadores distantes se dividen en superposiciones cuando miden un giro. Las violaciones de la desigualdad de Bell ya no son contraintuitivas, porque no está claro qué copia del observador B verá el observador A cuando comparen notas. Si la realidad incluye todos los diferentes resultados,

Este punto subraya el hecho de que el argumento de que el realismo es incompatible con la mecánica cuántica y la localidad depende de una formalización particular del concepto de realismo. En su forma más débil, la suposición que sustenta esa formalización particular se denomina definición contrafactual . Este es el supuesto de que los resultados de las mediciones que no se realizan son tan reales como los de las mediciones que se realizaron. La definición contrafactual es una propiedad no controvertida de todas las teorías físicas clásicas anteriores a la teoría cuántica, debido a su determinismo. Las interpretaciones de muchos mundos no solo son contrafactualmente indefinidas, sino que, de hecho, son indefinidas. Los resultados de todos los experimentos, incluso los que se han realizado, no están determinados de forma única.

Si uno elige rechazar la definición contrafactual, la realidad se ha hecho más pequeña y no hay problema de no localidad. Por otro lado, uno está introduciendo así aleatoriedad irreducible o intrínseca en nuestra imagen del mundo: la aleatoriedad que no puede ser "explicada" simplemente como el reflejo de nuestra ignorancia de las cantidades físicas subyacentes, variables. El no determinismo se convierte en una propiedad fundamental de la naturaleza.

Suponiendo una definición contrafactual, la realidad se ha ampliado y existe un problema de no localidad. Por otro lado, en la interpretación de la mecánica cuántica en muchos mundos, la realidad consiste solo en una función de onda evolutivamente determinista y la no localidad no es un problema.

También se han repetido las afirmaciones de que los argumentos de Bell son irrelevantes porque dependen de supuestos ocultos que, de hecho, son cuestionables. Por ejemplo, ET Jaynes ^[27] afirmó en 1989 que hay dos supuestos ocultos en el teorema de Bell que podrían limitar su generalidad. De acuerdo con él:

1. Bell interpretó la probabilidad condicional P (X | Y) como una inferencia causal, es decir, Y ejerció una inferencia causal sobre X en la realidad. Sin embargo, P (X | Y) en realidad solo significa inferencia lógica (inducción). Las causas no pueden viajar más rápido que la luz o hacia atrás en el tiempo, pero la deducción sí puede.
2. La desigualdad de Bell no se aplica a algunas posibles teorías de variables ocultas. Solo se aplica a una cierta clase de teorías locales de variables ocultas. De hecho, podría haberse perdido el tipo de teorías de variables ocultas que más le interesan a Einstein.

Sin embargo, Richard D. Gill ha argumentado que Jaynes entendió mal el análisis de Bell. Gill señala que en el mismo volumen de conferencia en el que Jaynes discute contra Bell, Jaynes confiesa sentirse extremadamente impresionado por una breve prueba de Steve Gull presentada en la misma conferencia, que las correlaciones singlete no se pueden reproducir mediante una simulación por computadora de un local. teoría de las variables ocultas. ^[28] Según Jaynes (escribiendo casi 30 años después de las contribuciones históricas de Bell), probablemente nos llevaría otros 30 años apreciar completamente el sorprendente resultado de Gull.

En 2006 surgió una serie de actividades sobre las implicaciones para el determinismo: el Teorema del libre albedrío ^[29], que establece que "la respuesta de una partícula de espín 1 a un experimento triple es gratuita, es decir, no es una función de las propiedades". de esa parte del universo que es anterior a esta respuesta con respecto a cualquier marco de inercia dado ". ^[30] Este teorema despertó la conciencia de una tensión entre el determinismo que gobierna completamente un experimento (por un lado) y que Alice y Bob son libres de elegir cualquier configuración que deseen para sus observaciones (por el otro). ^[31] [32] El filósofo David Hodgson apoya este teorema porque muestra que el determinismo no es científico, y esa mecánica cuántica permite a los observadores (al menos en algunos casos) la libertad de hacer observaciones de su elección, dejando así la puerta abierta para el libre albedrío. ^[33]

Observaciones generales [ editar ]

Las violaciones de las desigualdades de Bell, debido al entrelazamiento cuántico, proporcionan demostraciones casi definitivas de algo que ya se sospechaba: la física cuántica no puede ser representada por ninguna versión del cuadro clásico de la física. ^[34] Algunos elementos anteriores que parecían incompatibles con las imágenes clásicas incluían complementariedad y colapso de la función de onda . Las violaciones de Bell muestran que ninguna resolución de tales problemas puede evitar la máxima extrañeza del comportamiento cuántico. ^[35]

El documento EPR "identificó" las propiedades inusuales de los estados enredados , por ejemplo, el estado singlete mencionado anteriormente, que es la base para las aplicaciones actuales de la física cuántica, como la criptografía cuántica ; Una aplicación involucra la medición del entrelazamiento cuántico como una fuente física de bits para la inconsciente transferencia de Rabin.protocolo. Originalmente, se suponía que esta no-localidad era ilusoria, porque la interpretación estándar podía eliminar fácilmente la acción a distancia simplemente asignando a cada partícula los estados de giro definidos para todas las posibles direcciones de giro. El argumento de EPR era: por lo tanto, estos estados definidos existen, por lo tanto, la teoría cuántica está incompleta en el sentido de EPR, ya que no aparecen en la teoría. El teorema de Bell demostró que la predicción de "enredo" de la mecánica cuántica tiene un grado de no localidad que no puede explicarse por ninguna teoría clásica de las variables locales ocultas.