MECÁNICA CUÁNTICA

MECÁNICA CUÁNTICA

La mecánica cuántica y la física clásica [ editar ]

Las predicciones de la mecánica cuántica se han verificado experimentalmente con un grado de precisiónextremadamente alto . ^[48] De acuerdo con el principio de correspondencia entre la mecánica clásica y la mecánica cuántica, todos los objetos obedecen las leyes de la mecánica cuántica, y la mecánica clásica es solo una aproximación para grandes sistemas de objetos (o una mecánica cuántica estadística de una gran colección de partículas). ^[49] Las leyes de la mecánica clásica se derivan así de las leyes de la mecánica cuántica como un promedio estadístico en el límite de grandes sistemas o grandes números cuánticos . ^[50] Sin embargo, los sistemas caóticos no tienen buenos números cuánticos, y el caos cuánticoestudia la relación entre las descripciones clásica y cuántica en estos sistemas.

La coherencia cuántica es una diferencia esencial entre las teorías clásica y cuántica, como lo ilustra la paradoja de Einstein-Podolsky-Rosen (EPR)  : un ataque a una cierta interpretación filosófica de la mecánica cuántica mediante una apelación al realismo local . ^[51] La interferencia cuántica consiste en sumar amplitudes de probabilidad , mientras que las "ondas" clásicas deducen que hay una suma de intensidades . Para cuerpos microscópicos, la extensión del sistema es mucho más pequeña que la longitud de coherencia , lo que da lugar al enredo de largo alcance y otros fenómenos no locales característicos de los sistemas cuánticos. ^[52]La coherencia cuántica no suele ser evidente a escalas macroscópicas, aunque puede ocurrir una excepción a esta regla a temperaturas extremadamente bajas (es decir, cerca del cero absoluto ) a las que el comportamiento cuántico puede manifestarse macroscópicamente. ^[53] Esto está de acuerdo con las siguientes observaciones:

• Muchas propiedades macroscópicas de un sistema clásico son una consecuencia directa del comportamiento cuántico de sus partes. Por ejemplo, la estabilidad de la materia a granel (que consiste en átomos y moléculas que rápidamente se colapsarían solo por fuerzas eléctricas), la rigidez de los sólidos y las propiedades mecánicas, térmicas, químicas, ópticas y magnéticas de la materia son todos resultados de la interacción de Cargas eléctricas bajo las reglas de la mecánica cuántica. ^[54]
• Mientras que el comportamiento aparentemente "exótico" de la materia planteado por la mecánica cuántica y la teoría de la relatividad se hace más evidente cuando se trata de partículas de tamaño extremadamente pequeño o velocidades que se aproximan a la velocidad de la luz , las leyes de la física clásica, a menudo consideradas " newtonianas ", siguen siendo precisas en predecir el comportamiento de la gran mayoría de objetos "grandes" (en el orden del tamaño de moléculas grandes o más grandes) a velocidades mucho más pequeñas que la velocidad de la luz . ^[55]

Interpretación de Copenhague de la cinemática cuántica versus clásica [ editar ]

Una gran diferencia entre la mecánica clásica y la cuántica es que utilizan descripciones cinemáticas muy diferentes. ^[56]

En la visión madura de Niels Bohr , se requiere que los fenómenos de la mecánica cuántica sean experimentos, con descripciones completas de todos los dispositivos para el sistema, preparativos, intermediarios y, finalmente, de medición. Las descripciones están en términos macroscópicos, expresados ​​en lenguaje ordinario, complementados con los conceptos de la mecánica clásica. ^{[57] [58] [59] [60]}La condición inicial y la condición final del sistema se describen respectivamente por valores en un espacio de configuración, por ejemplo, un espacio de posición, o algún espacio equivalente, como un espacio de momento. La mecánica cuántica no admite una descripción completamente precisa, en términos de posición y momento, de una condición inicial o "estado" (en el sentido clásico de la palabra) que apoyaría una predicción causista y determinista precisa de una condición final. ^[61] [62] En este sentido, defendido por Bohr en sus escritos maduros, un fenómeno cuántico es un proceso, un pasaje de la condición inicial a la final, no un "estado" instantáneo en el sentido clásico de esa palabra. ^[63] [64]Por lo tanto, hay dos tipos de procesos en la mecánica cuántica: estacionarios y transicionales. Para un proceso estacionario, la condición inicial y final son las mismas. Para una transición, son diferentes. Obviamente, por definición, si solo se da la condición inicial, el proceso no está determinado. ^[61] Dada su condición inicial, la predicción de su condición final es posible, de manera causal pero solo probabilística, porque la ecuación de Schrödinger es determinista para la evolución de la función de onda, pero la función de onda describe el sistema solo de forma probabilística. ^[65] [66]

Para muchos experimentos, es posible pensar que las condiciones iniciales y finales del sistema son una partícula. En algunos casos, parece que hay potencialmente varias vías o trayectorias espacialmente distintas por las cuales una partícula podría pasar de la condición inicial a la final. Es una característica importante de la descripción cinemática cuántica que no permite una declaración definida única de cuál de esas vías se sigue realmente. Solo las condiciones iniciales y finales son definitivas y, como se indica en el párrafo anterior, se definen solo con la precisión que permite la descripción del espacio de configuración o su equivalente. En todos los casos para los que se necesita una descripción cinemática cuántica, siempre hay una razón convincente para esta restricción de la precisión cinemática. Un ejemplo de tal razón es que para que una partícula se encuentre experimentalmente en una posición definida, debe mantenerse inmóvil; para que se descubra experimentalmente que tiene un impulso definido, debe tener movimiento libre; estos dos son lógicamente incompatibles^[67] [68]

La cinemática clásica no exige principalmente una descripción experimental de sus fenómenos. Permite una descripción completamente precisa de un estado instantáneo por un valor en el espacio de fase, el producto cartesiano de configuración y espacios de momento. Esta descripción simplemente asume o imagina un estado como una entidad físicamente existente sin preocuparse por su capacidad de medición experimental. Tal descripción de una condición inicial, junto con las leyes de movimiento de Newton, permite una predicción determinista y causal precisa de una condición final, con una trayectoria de paso definida. La dinámica hamiltoniana se puede utilizar para esto. La cinemática clásica también permite la descripción de un proceso análogo a la descripción de condición inicial y final utilizada por la mecánica cuántica. Mecánica lagrangianase aplica a esto ^[69] Para los procesos que deben tomarse en cuenta las acciones de un pequeño número de constantes de Planck , la cinemática clásica no es adecuada; La mecánica cuántica es necesaria.

La relatividad general y la mecánica cuántica [ editar ]

Incluso con los postulados definitorios de la teoría de la relatividad general y la teoría cuántica de Einstein que están respaldados indiscutiblemente por pruebas empíricas rigurosas y repetidas , y si bien no se contradicen directamente entre sí teóricamente (al menos con respecto a sus afirmaciones primarias), han demostrado ser extremadamente Difícil de incorporar en un modelo coherente y cohesivo. ^[70]

La gravedad es despreciable en muchas áreas de la física de partículas, por lo que la unificación entre la relatividad general y la mecánica cuántica no es un problema urgente en esas aplicaciones particulares. Sin embargo, la falta de una teoría correcta de la gravedad cuántica es un tema importante en la cosmología física y la búsqueda por parte de los físicos de una elegante " Teoría del Todo " (TOE). En consecuencia, la resolución de las inconsistencias entre ambas teorías ha sido un objetivo importante de la física de los siglos XX y XXI. Muchos físicos prominentes, incluido Stephen Hawking , han trabajado durante muchos años en el intento de descubrir una teoría subyacente a todo.. Este TOE combinaría no solo los diferentes modelos de física subatómica, sino que también derivaría las cuatro fuerzas fundamentales de la naturaleza : la fuerza fuerte , el electromagnetismo, la fuerza débil y la gravedad , de una sola fuerza o fenómeno. Si bien Stephen Hawking fue inicialmente un creyente en la Teoría del Todo, después de considerar el Teorema de Incompletitud de Gödel , concluyó que no se puede obtener, y lo ha declarado públicamente en su conferencia "Gödel y el fin de la física" (2002). ^[71]

Los intentos de una teoría del campo unificado [ editar ]

Artículo principal: Gran teoría unificada.

La búsqueda para unificar las fuerzas fundamentales a través de la mecánica cuántica aún está en curso. La electrodinámica cuántica (o "electromagnetismo cuántico"), que actualmente es (al menos en el régimen perturbativo) la teoría física más probada en competencia con la relatividad general, ^[72] [73] se ha fusionado con éxito con la fuerza nuclear débil en el La fuerza electrodébil y el trabajo se está realizando actualmente para fusionar la electrodébil y la fuerza fuerte en la fuerza electrostrong . Las predicciones actuales indican que, alrededor de 10 ¹⁴ GV, las tres fuerzas mencionadas anteriormente se fusionan en un solo campo unificado. ^[74]Más allá de esta "gran unificación", se especula que puede ser posible fusionar la gravedad con las otras tres simetrías de calibre, que se espera que ocurran en aproximadamente 10 ¹⁹ GeV. Sin embargo, y mientras la relatividad especial se incorpora parsimoniosamente a la electrodinámica cuántica, la relatividad generalexpandida , actualmente la mejor teoría que describe la fuerza de gravitación, no se ha incorporado completamente a la teoría cuántica. Uno de los que buscan un TOE coherente es Edward Witten , un físico teórico que formuló la teoría M , que trata de describir la teoría de cuerdas basada en una base supersimétrica . La teoría M postula que nuestro aparente espacio-tiempo 4-dimensional es, en realidad, un espacio-tiempo de 11 dimensiones que contiene 10 dimensiones espaciales y 1 dimensión de tiempo, aunque 7 de las dimensiones espaciales son - en energías más bajas - completamente "compactas" (o infinitamente curvadas) y no fácilmente susceptibles de medición o sondeo.

Otra teoría popular es la gravedad cuántica de bucle (LQG), una teoría propuesta por primera vez por Carlo Rovelli que describe las propiedades cuánticas de la gravedad. También es una teoría del espacio cuántico y del tiempo cuántico , porque en la relatividad general la geometría del espacio-tiempo es una manifestación de la gravedad . LQG es un intento de fusionar y adaptar la mecánica cuántica estándar y la relatividad generalestándar.. El resultado principal de la teoría es una imagen física del espacio donde el espacio es granular. La granularidad es una consecuencia directa de la cuantización. Tiene la misma naturaleza de la granularidad de los fotones en la teoría cuántica del electromagnetismo o los niveles discretos de la energía de los átomos. Pero aquí es el espacio mismo lo que es discreto. Más precisamente, el espacio puede verse como un tejido o red extremadamente fino "tejido" de bucles finitos. Estas redes de bucles se denominan redes de espín . La evolución de una red de espín a lo largo del tiempo se llama espuma de espín. El tamaño predicho de esta estructura es la longitud de Planck , que es aproximadamente 1.616 × 10 ⁻³⁵ m. Según la teoría, no hay un significado para la longitud más corta que esto (véase la escala de Planckenergía). Por lo tanto, LQG predice que no solo la materia, sino también el espacio en sí, tiene una estructura atómica.

Implicaciones filosóficas [ editar ]

Artículo principal: Interpretaciones de la mecánica cuántica.

Desde su inicio, los numerosos aspectos y resultados contraintuitivos de la mecánica cuántica han provocado fuertes debates filosóficos y muchas interpretaciones . Incluso las cuestiones fundamentales, como las reglasbásicas de Max Born relativas a las amplitudes de probabilidad y las distribuciones de probabilidad , tardaron décadas en ser apreciadas por la sociedad y muchos científicos destacados. Richard Feynman dijo una vez: "Creo que puedo decir con seguridad que nadie entiende la mecánica cuántica". ^[75] Según Steven Weinberg , "En mi opinión, ahora no hay una interpretación completamente satisfactoria de la mecánica cuántica".^[76]

La interpretación de Copenhague  , debida en gran medida a Niels Bohr y Werner Heisenberg, sigue siendo la más aceptada entre los físicos, unos 75 años después de su enunciación. De acuerdo con esta interpretación, la naturaleza probabilística de la mecánica cuántica no es una característica temporal que eventualmente será reemplazada por una teoría determinista, sino que debe considerarse como una renuncia final a la idea clásica de "causalidad". También se cree que cualquier aplicación bien definida del formalismo mecánico cuántico siempre debe hacer referencia a la disposición experimental, debido a la naturaleza conjugada de la evidencia obtenida en diferentes situaciones experimentales.

Albert Einstein, uno de los fundadores de la teoría cuántica, no aceptó algunas de las interpretaciones más filosóficas o metafísicas de la mecánica cuántica, como el rechazo del determinismo y la causalidad . Se lo cita como famoso, en respuesta a este aspecto, "Dios no juega con los dados". ^[77]Rechazó el concepto de que el estado de un sistema físico depende de la disposición experimental para su medición. Sostuvo que un estado de naturaleza ocurre por derecho propio, independientemente de si se puede observar o cómo. Desde ese punto de vista, está respaldado por la definición actualmente aceptada de un estado cuántico, que permanece invariante bajo la elección arbitraria del espacio de configuración para su representación, es decir, la forma de observación. También sostuvo que la mecánica cuántica subyacente debería haber una teoría que exprese completa y directamente la regla contra la acción a distancia ; En otras palabras, insistió en el principio de localidad.. Consideró, pero rechazó por razones teóricas, una propuesta particular de variables ocultas para obviar el indeterminismo o la causalidad de la medición de la mecánica cuántica. Consideró que la mecánica cuántica era actualmente una teoría válida pero no definitiva para los fenómenos cuánticos. Pensó que su futura sustitución requeriría profundos avances conceptuales, y no se produciría rápida ni fácilmente. Los debates de Bohr-Einsteinproporcionan una crítica vibrante de la Interpretación de Copenhague desde un punto de vista epistemológico . Al defender sus puntos de vista, produjo una serie de objeciones, la más famosa de las cuales se conoce como la paradoja de Einstein-Podolsky-Rosen .

John Bell demostró que esta paradoja de EPR llevó a diferencias experimentalmente comprobables entre la mecánica cuántica y las teorías que se basan en variables ocultas agregadas. Se han realizado experimentosque confirman la precisión de la mecánica cuántica, lo que demuestra que la mecánica cuántica no se puede mejorar mediante la adición de variables ocultas. ^[78]Los experimentos iniciales de Alain Aspect en 1982, y muchos experimentos posteriores desde entonces, han verificado definitivamente el entrelazamiento cuántico. A principios de la década de 1980, los experimentos demostraron que tales desigualdades se violaron en la práctica, de modo que de hecho existían correlaciones del tipo sugerido por la mecánica cuántica. Al principio, solo parecían efectos esotéricos aislados, pero a mediados de la década de 1990, estaban siendo codificados en el campo de la teoría de la información cuántica, y llevaron a construcciones con nombres como criptografía cuántica y teletransportación cuántica . ^[79]

El enredo, como se demuestra en los experimentos tipo Bell, no viola, sin embargo, la causalidad , ya que no ocurre transferencia de información. El entrelazamiento cuántico forma la base de la criptografía cuántica , que se propone para su uso en aplicaciones comerciales de alta seguridad en la banca y el gobierno.

La interpretación de los mundos múltiples de Everett , formulada en 1956, sostiene que todas las posibilidades descritas por la teoría cuántica ocurren simultáneamente en un multiverso compuesto de universos paralelos en su mayoría independientes. ^[80] Esto no se logra mediante la introducción de algún "nuevo axioma" a la mecánica cuántica, sino por el contrario, eliminando el axioma del colapso del paquete de ondas. Todos los posibles estados consistentes del sistema medido y el aparato de medición (incluido el observador) están presentes en un físico real , no solo formalmente matemático, como en otras interpretaciones, superposición cuántica. Tal superposición de combinaciones de estados consistentes de diferentes sistemas se denomina estado entrelazado . Si bien el multiverso es determinista, percibimos un comportamiento no determinista gobernado por probabilidades, porque solo podemos observar el universo (es decir, la contribución del estado consistente a la superposición mencionada anteriormente) que nosotros, como observadores, habitamos. La interpretación de Everett es perfectamente consistente con los experimentos de John Bell y los hace intuitivamente comprensibles. Sin embargo, de acuerdo con la teoría de la decoherencia cuántica , estos "universos paralelos" nunca serán accesibles para nosotros. La inaccesibilidad se puede entender de la siguiente manera: una vez que se realiza una medición, el sistema medido se enreda con ambosel físico que lo midió y una gran cantidad de otras partículas, algunas de las cuales son fotones que se alejan a la velocidad de la luz hacia el otro extremo del universo. Para probar que la función de onda no colapsó, uno tendría que recuperar todas estas partículas y medirlas, junto con el sistema que se midió originalmente. Esto no solo es completamente impráctico, sino que incluso si uno pudiera hacer esto teóricamente, tendría que destruir cualquier evidencia de que la medición original tuvo lugar (incluida la memoria del físico). A la luz de estas pruebas de Bell , Cramer (1986) formuló su interpretación transaccional ^[81]que es único en proporcionar una explicación física para la regla Born . ^{[82] La}mecánica cuántica relacional apareció a fines de la década de 1990 como la derivada moderna de la Interpretación de Copenhague .

Aplicaciones [ editar ]

La mecánica cuántica ha tenido un éxito enorme ^[83] al explicar muchas de las características de nuestro universo. La mecánica cuántica es a menudo la única teoría que puede revelar los comportamientos individuales de las partículas subatómicas que forman todas las formas de la materia ( electrones , protones , neutrones , fotones y otros). La mecánica cuántica ha influido fuertemente en las teorías de cuerdas , candidatos para una Teoría del Todo (ver reduccionismo ).

La mecánica cuántica también es de importancia crítica para comprender cómo los átomos individuales se unen mediante un enlace covalente para formar moléculas . La aplicación de la mecánica cuántica a la química se conoce como química cuántica. La mecánica cuántica también puede proporcionar una visión cuantitativa de losprocesos de enlace iónico y covalente al mostrar explícitamente qué moléculas son energéticamente favorables a las otras y las magnitudes de las energías involucradas. ^[84] Además, la mayoría de los cálculos realizados en la química computacional moderna se basan en la mecánica cuántica.

En muchos aspectos, la tecnología moderna opera a una escala donde los efectos cuánticos son significativos.

Electrónica [ editar ]

Muchos dispositivos electrónicos modernos están diseñados utilizando mecánica cuántica. Los ejemplos incluyen el láser , el transistor (y por lo tanto el microchip ), el microscopio electrónico y la imagen de resonancia magnética (MRI). El estudio de los semiconductores condujo a la invención del diodo y el transistor , que son partes indispensables de los sistemas electrónicos modernos, computadoras y dispositivos de telecomunicaciones . Otra aplicación es para hacer diodos láser y diodos emisores de luz que son una fuente de luz de alta eficiencia.

Un mecanismo de trabajo de un dispositivo de diodo de túnel resonante , basado en el fenómeno del túnel cuántico a través de barreras potenciales . (Izquierda: diagrama de banda ; Centro: coeficiente de transmisión ; Derecha: características de voltaje-corriente) Como se muestra en el diagrama de banda (izquierda), aunque hay dos barreras, los electrones todavía se conectan a través de los estados confinados entre dos barreras (centro), conduciendo corriente.

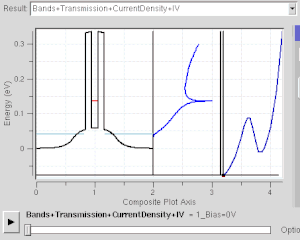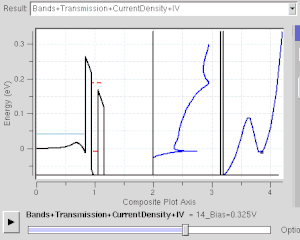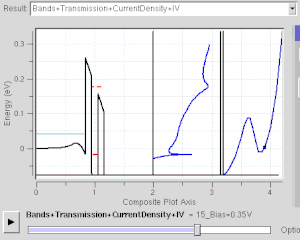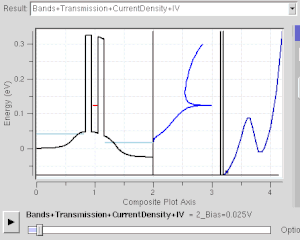
Muchos dispositivos electrónicos funcionan bajo efecto de tunelización cuántica . Incluso existe en el simple interruptor de la luz . El interruptor no funcionaría si los electrones no pudieran un túnel cuántico a través de la capa de oxidación en las superficies de contacto metálicas. Los chips de memoria flash que se encuentran en las unidades USB usan túneles cuánticos para borrar sus celdas de memoria. Algunos dispositivos de resistencia diferencial negativa también utilizan un efecto de túnel cuántico, como el diodo de túnel resonante . A diferencia de los diodos clásicos, su corriente es transportada por túneles resonantes a través de dos o más barreras potenciales(ver figura derecha). Su comportamiento de resistencia negativa solo puede entenderse con la mecánica cuántica: a medida que el estado confinado se acerca al nivel de Fermi , aumenta la corriente del túnel. A medida que se aleja, la corriente disminuye. La mecánica cuántica es necesaria para comprender y diseñar dichos dispositivos electrónicos.

La criptografía [ editar ]

Los investigadores actualmente están buscando métodos robustos para manipular directamente los estados cuánticos. Se están haciendo esfuerzos para desarrollar más a fondo la criptografía cuántica , que teóricamente permitirá una transmisión segura y segura de la información.

Una ventaja inherente producida por la criptografía cuántica en comparación con la criptografía clásica es la detección de escuchas pasivas . Este es un resultado natural del comportamiento de los bits cuánticos; debido al efecto observador , si se observara un bit en un estado de superposición, el estado de superposición colapsaría en un estado propio . Debido a que el destinatario deseado esperaba recibir el bit en un estado de superposición, el destinatario deseado sabría que hubo un ataque, porque el estado del bit ya no estaría en una superposición. ^[85]

La computación cuántica [ editar ]

Otro objetivo es el desarrollo de computadoras cuánticas , que se espera que realicen ciertas tareas computacionales de manera exponencial más rápida que las computadoras clásicas . En lugar de usar bits clásicos, las computadoras cuánticas usan qubits , que pueden estar en superposiciones de estados. Los programadores cuánticos pueden manipular la superposición de qubits para resolver problemas que la computación clásica no puede hacer de manera efectiva, como buscar bases de datos sin clasificar o factorización de enteros . IBM afirma que el advenimiento de la computación cuántica puede avanzar en los campos de la medicina, la logística, los servicios financieros, la inteligencia artificial y la seguridad en la nube. ^[86]

Otro tema de investigación activo es la teletransportación cuántica , que trata sobre técnicas para transmitir información cuántica a través de distancias arbitrarias.

Efectos cuánticos macroscópicos [ editar ]

Mientras que la mecánica cuántica se aplica principalmente a los regímenes atómicos más pequeños de la materia y la energía, algunos sistemas exhiben efectos mecánicos cuánticos a gran escala. Superfluidez , el flujo sin fricción de un líquido a temperaturas cercanas al cero absoluto , es un ejemplo bien conocido. Así es el fenómeno estrechamente relacionado de la superconductividad , el flujo sin fricción de un gas de electrones en un material conductor (una corriente eléctrica ) a temperaturas suficientemente bajas. El efecto Hall cuántico fraccional es un estado ordenado topológico que corresponde a patrones de entrelazamiento cuántico de largo alcance . ^[87] Los estados con diferentes órdenes topológicos (o diferentes patrones de enredos de largo alcance) no pueden cambiar entre sí sin una transición de fase.

La teoría cuántica [ editar ]

La teoría cuántica también proporciona descripciones precisas para muchos fenómenos previamente inexplicables, como la radiación del cuerpo negro y la estabilidad de los orbitales de los electrones en los átomos. También ha brindado información sobre el funcionamiento de muchos sistemas biológicos diferentes , incluidos los receptores de olores y las estructuras de proteínas . ^[88] El trabajo reciente sobre la fotosíntesis ha proporcionado evidencia de que las correlaciones cuánticas desempeñan un papel esencial en este proceso fundamental de las plantas y muchos otros organismos. ^[89] Aun así, la física clásica.a menudo puede proporcionar buenas aproximaciones a los resultados obtenidos de otra manera por la física cuántica, típicamente en circunstancias con grandes cantidades de partículas o grandes cantidades cuánticas . Dado que las fórmulas clásicas son mucho más simples y fáciles de calcular que las fórmulas cuánticas, las aproximaciones clásicas se usan y se prefieren cuando el sistema es lo suficientemente grande como para hacer que los efectos de la mecánica cuántica sean insignificantes.

Ejemplos [ editar ]

Partícula libre [ editar ]

Por ejemplo, considere una partícula libre . En la mecánica cuántica, una materia libre se describe mediante una función de onda. Las propiedades de las partículas de la materia se hacen evidentes cuando medimos su posición y velocidad. Las propiedades de onda de la materia se hacen evidentes cuando medimos sus propiedades de onda como la interferencia. La característica de dualidad onda-partícula se incorpora en las relaciones de coordenadas y operadores en la formulación de la mecánica cuántica. Dado que la materia es libre (no está sujeta a ninguna interacción), su estado cuántico se puede representar como una onda de forma arbitraria y se extiende sobre el espacio como una función de onda . La posición y el momento de la partícula son observables . losEl principio de incertidumbre establece que tanto la posición como el impulso no pueden medirse simultáneamente con total precisión. Sin embargo, uno puede medir la posición (solo) de una partícula libre en movimiento, creando un estado propio de posición con una función de onda que es muy grande (un delta de Dirac ) en una posición particular xy cero en cualquier otra parte. Si se realiza una medición de posición en una función de onda de este tipo, la x resultante se obtendrá con un 100% de probabilidad (es decir, con total certeza o precisión completa). Esto se denomina un estado propio de posición o, en términos matemáticos, un estado propio de posición generalizada ( eigendistribución ). Si la partícula está en un estado propio de posición, entonces su momento es completamente desconocido. Por otro lado, si la partícula está en un estado propio de impulso, entonces su posición es completamente desconocida. ^[90] En un estado propio de momento que tiene una forma de onda plana , se puede mostrar que la longitud de onda es igual a h / p , donde h es la constante de Planck y p es el momento del estado propio . ^[91]

Partícula en una caja [ editar ]

Caja de energía potencial unidimensional (o pozo potencial infinito)

Artículo principal: Partícula en una caja.

La partícula en una caja de energía potencial unidimensional es el ejemplo más simple matemáticamente donde las restricciones conducen a la cuantización de los niveles de energía. El cuadro se define como tener energía potencial cero en cualquier parte dentro de una determinada región y, por lo tanto, energía potencial infinita en cualquier lugar fuera de esa región. Para el caso unidimensional en el$${\ displaystyle x}dirección, la ecuación de Schrödinger independiente del tiempo se puede escribir ^[92]

$${\ displaystyle - {\ frac {\ hbar ^ {2}} {2m}} {\ frac {d ^ {2} \ psi} {dx ^ {2}}} = E \ psi.}

Con el operador diferencial definido por

$${\ displaystyle {\ hat {p}} _ {x} = - i \ hbar {\ frac {d} {dx}}}

La ecuación anterior es evocadora del análogo clásico de la energía cinética ,

$${\ displaystyle {\ frac {1} {2m}} {\ hat {p}} _ {x} ^ {2} = E,}

con estado $${\ displaystyle \ psi} en este caso teniendo energía $${\ displaystyle E} Coincidiendo con la energía cinética de la partícula.

Las soluciones generales de la ecuación de Schrödinger para la partícula en una caja son

$${\ displaystyle \ psi (x) = Ae ^ {ikx} + Be ^ {- ikx} \ qquad \ qquad E = {\ frac {\ hbar ^ {2} k ^ {2}} {2m}}}

o, a partir de la fórmula de Euler ,

$${\ displaystyle \ psi (x) = C \ sin kx + D \ cos kx. \!}

Los infinitos muros potenciales de la caja determinan los valores de C , D y k en x = 0 y x = L donde ψ debe ser cero. Así, en x = 0 ,

$${\ displaystyle \ psi (0) = 0 = C \ sin 0 + D \ cos 0 = D \!}

y D = 0 . En x = L ,

$${\ displaystyle \ psi (L) = 0 = C \ sin kL. \!}

en el que C no puede ser cero, ya que esto podría entrar en conflicto con la interpretación de Born. Por lo tanto, como sen ( kL ) = 0 , kL debe ser un múltiplo entero de π ,

$${\ displaystyle k = {\ frac {n \ pi} {L}} \ qquad \ qquad n = 1,2,3, \ ldots.}

La cuantización de los niveles de energía se deriva de esta restricción en k , ya que

$${\ displaystyle E = {\ frac {\ hbar ^ {2} \ pi ^ {2} n ^ {2}} {2mL ^ {2}}} = {\ frac {n ^ {2} h ^ {2} } {8mL ^ {2}}}.}

La energía del estado fundamental de las partículas es E ₁ para n = 1.

La energía de la partícula en el estado n ^th es E _n = n ² E ₁ , n = 2,3,4, .....

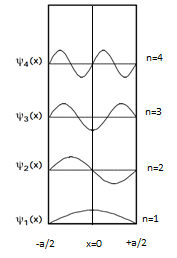
Partícula en un recuadro con condición de contorno V (x) = 0 -a / 2

Una partícula en una caja con un pequeño cambio en la condición de contorno.

En esta condición, la solución general será la misma, habrá un pequeño cambio en el resultado final, ya que se cambian las condiciones de contorno.

$${\ displaystyle \ psi (x) = C \ sin kx + D \ cos kx. \!}

En x = 0, la función de onda no es realmente cero en todo el valor de n.

Claramente, a partir del gráfico de variación de función de onda que tenemos,

En n = 1,3,4, ...... la función de onda sigue una curva de coseno con x = 0 como origen

En n = 2,4,6, ...... la función de onda sigue una curva sinusoidal con x = 0 como origen

Variación de la función de onda con x y n.

De esta observación podemos concluir que la función de onda es alternativamente senoidal y coseno.

Así que en este caso la ecuación de onda resultante es

ψ _n (x) = Acos (k _n x) n = 1,3,5, .............

= Bsin (k _n x) n = 2,4,6, .............

Bien potencial finito [ editar ]

Artículo principal: potencial finito y pozo.

Un pozo potencial finito es la generalización del problema del pozo infinito potencial a pozos potenciales que tienen una profundidad finita.

El problema del pozo del potencial finito es matemáticamente más complicado que el problema de la infinita partícula en una caja, ya que la función de onda no se fija a cero en las paredes del pozo. En cambio, la función de onda debe satisfacer condiciones de límites matemáticos más complicados, ya que no es cero en regiones fuera del pozo.

Barrera de potencial rectangular [ editar ]

Artículo principal: Barrera de potencial rectangular.

Este es un modelo para el efecto de túnel cuántico que desempeña un papel importante en el rendimiento de las tecnologías modernas, como la memoria flash y la microscopía de exploración de túneles . La tunelización cuántica es fundamental para los fenómenos físicos implicados en las superlatticias .

Oscilador armónico [ editar ]

Artículo principal: Oscilador armónico cuántico.

Algunas trayectorias de un oscilador armónico (es decir, una bola unida a un resorte ) en mecánica clásica (AB) y mecánica cuántica (CH). En mecánica cuántica, la posición de la bola está representada por una onda (llamada función de onda ), con la parte real mostrada en azul y la parte imaginaria mostrada en rojo. Algunas de las trayectorias (como C, D, E y F) son ondas estacionarias (o " estados estacionarios"). Cada frecuencia de onda estacionaria es proporcional a un posible nivel de energía del oscilador. Esta "cuantización de energía" no ocurre en la física clásica, donde el oscilador puede tenercualquier energia

Como en el caso clásico, el potencial del oscilador armónico cuántico viene dado por

$${\ displaystyle V (x) = {\ frac {1} {2}} m \ omega ^ {2} x ^ {2}.}

Este problema puede tratarse resolviendo directamente la ecuación de Schrödinger, que no es trivial, o usando el "método de escalera" más elegante propuesto por primera vez por Paul Dirac. Los estados propios están dados por

$${\ displaystyle \ psi _ {n} (x) = {\ sqrt {\ frac {1} {2 ^ {n} \, n!}}} \ cdot \ left ({\ frac {m \ omega} {\ pi \ hbar}} \ right) ^ {1/4} \ cdot e ^ {- {\ frac {m \ omega x ^ {2}} {2 \ hbar}}} \ cdot H_ {n} \ left ({ \ sqrt {\ frac {m \ omega} {\ hbar}}} x \ right), \ qquad}

$${\ displaystyle n = 0,1,2, \ ldots.}

donde H _n son los polinomios de Hermite

$${\ displaystyle H_ {n} (x) = (- 1) ^ {n} e ^ {x ^ {2}} {\ frac {d ^ {n}} {dx ^ {n}}} \ left (e ^ {- x ^ {2}} \ derecha),}

y los niveles de energía correspondientes son

$${\ displaystyle E_ {n} = \ hbar \ omega \ left (n + {1 \ over 2} \ right).}

Este es otro ejemplo que ilustra la cuantificación de la energía para estados unidos.

Paso potencial [ editar ]

Artículo principal: Solución de la ecuación de Schrödinger para un potencial de paso

Dispersión en un paso de potencial finito de altura V ₀ , mostrado en verde. Se indican las amplitudes y la dirección de las ondas hacia la izquierda y hacia la derecha. El amarillo es la onda incidente, el azul se refleja y las ondas transmitidas, el rojo no se produce. E > V ₀ para esta figura.

El potencial en este caso está dado por:

{\ displaystyle V (x) = {\ begin {cases} 0, & x <0 0.="" amp="" cases="" end="" font="" geq="" v_="" x="">

Las soluciones son superposiciones de ondas hacia la izquierda y hacia la derecha:

{\ displaystyle \ psi _ {1} (x) = {\ frac {1} {\ sqrt {k_ {1}}}} \ left (A _ {\ rightarrow} e ^ {ik_ {1} x} + A_ { \ leftarrow} e ^ {- ik_ {1} x} \ derecha) \ qquad x <0 font="">

y

{\ displaystyle \ psi _ {2} (x) = {\ frac {1} {\ sqrt {k_ {2}}}} \ left (B _ {\ rightarrow} e ^ {ik_ {2} x} + B_ { \ leftarrow} e ^ {- ik_ {2} x} \ derecha) \ qquad x> 0},

con los coeficientes A y B determinados a partir de las condiciones de contorno e imponiendo una derivadacontinua en la solución, y donde los vectores de onda están relacionados con la energía a través de

$${\ displaystyle k_ {1} = {\ sqrt {2mE / \ hbar ^ {2}}}}

y

$${\ displaystyle k_ {2} = {\ sqrt {2m (E-V_ {0}) / \ hbar ^ {2}}}}.