MECÁNICA CUÁNTICA

El efecto Aharonov-Casher es un fenómeno mecánico cuántico predicho en 1984 en el que un dipolo magnético móvil se ve afectado por un campo eléctrico . Es dual al efecto Aharonov-Bohm , en el cual la fase cuántica de una partícula cargada depende de qué lado de un tubo de flujo magnético atraviesa. En el efecto Aharonov-Casher, la partícula tiene un momento magnético y los tubos se cargan en su lugar. Se observó en un inferómetro de neutrones gravitacional en 1989 (Cimmino et al.) Y más tarde por interferencia de fluxón de vórtices magnéticos en las uniones de Josephson (Elion et al.). También se ha visto con electrones y átomos.

En ambos efectos la partícula adquiere un cambio de fase ($${\ displaystyle \ varphi}) mientras viajaba por algún camino p . En el efecto Aharonov-Bohm es

$${\ displaystyle \ varphi _ {AB} = {\ frac {q} {\ hbar}} \ int _ {P} \ mathbf {A} \ cdot d \ mathbf {x}}

Mientras que para el efecto Aharonov-Casher es

$${\ displaystyle \ varphi _ {AC} = {\ frac {1} {\ hbar c ^ {2}}} \ int _ {P} (\ mathbf {E} \ times {\ boldsymbol {\ mu}}) \ cdot d \ mathbf {x}}

dónde $${\ displaystyle q} es su cargo y $${\ displaystyle {\ boldsymbol {\ mu}}}Es el momento magnético. Los efectos se han observado juntos (Bogachek y Landman).

los diagramas de momento angular , o más precisamente desde un punto de vista matemático , los gráficos de momento angular son un método esquemático para representar los estados cuánticos de momento angularde un sistema cuántico que permiten realizar cálculos. hecho simbólicamente. Más específicamente, las flechas codifican estados de momento angular en notación bra-ket e incluyen la naturaleza abstracta del estado, como los productos tensoriales y las reglas de transformación.

La notación es paralela a la idea de la notación gráfica de Penrose y los diagramas de Feynman . Los diagramas se componen de flechas y vértices con números cuánticos como etiquetas, de ahí el término alternativo " gráficos ". El sentido de cada flecha está relacionado con la conjugación hermitiana , que corresponde aproximadamente a la inversión temporal de los estados del momento angular (véase la ecuación de Schrödinger ). La notación esquemática es un tema considerablemente grande en sí mismo con una serie de características especializadas. Este artículo presenta los conceptos básicos.

Fueron desarrollados principalmente por Adolfas Jucys (a veces traducido como Yutsis) en el siglo XX.

Equivalencia entre la notación de Dirac y los diagramas de Jucys [ editar ]

Estados de momento angular [ editar ]

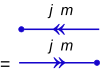
El vector de estado cuántico de una sola partícula con momento angular total número cuántico j y número cuántico magnético total m = j , j - 1, ..., - j + 1, - j , se denota como un cet | j , m ⟩ . Como diagrama se trata de una flecha de una sola cabeza.

Simétricamente, el sujetador correspondiente es ⟨ j , m | . En forma de diagrama, se trata de una flecha de dospuntas, que apunta en dirección opuesta al cet.

En cada caso;

• los números cuánticos j , m se etiquetan a menudo junto a las flechas para referirse a un estado de momento angular específico,
• las puntas de flecha casi siempre se colocan en el centro de la línea, en lugar de en la punta,
• Los signos de igual "=" se colocan entre diagramas equivalentes, exactamente igual que para varias expresiones algebraicas iguales entre sí.

Los diagramas más básicos son para kets y sostenes:

Ket | j , m ⟩

Sujetador ⟨ j , m |

Las flechas se dirigen hacia o desde los vértices, un estado que se transforma de acuerdo con:

• una representación estándar es designada por una línea orientada que deja un vértice,
• una representación de contraste y estándar se representa como una línea que ingresa a un vértice.

Como regla general, las flechas se siguen en el mismo sentido. En la representación de contraste y estándar , se utiliza el operador de inversión de tiempo , indicado aquí por T. Es unitario, lo que significa que el conjugado hermitiano T ^† es igual al operador inverso T ⁻¹ , que es T ^† = T ⁻¹ . Su acción sobre el operador de posición lodeja invariante:

$${\ displaystyle T {\ hat {\ mathbf {x}}} T ^ {\ dagger} = {\ hat {\ mathbf {x}}}}

pero el operador de momento lineal se vuelve negativo:

$${\ displaystyle T {\ hat {\ mathbf {p}}} T ^ {\ dagger} = - {\ hat {\ mathbf {p}}}}

y el operador de giro se vuelve negativo:

$${\ displaystyle T {\ hat {\ mathbf {S}}} T ^ {\ dagger} = - {\ hat {\ mathbf {S}}}}

Dado que el operador del momento angular orbital es L = x × p , esto también debe volverse negativo:

$${\ displaystyle T {\ hat {\ mathbf {L}}} T ^ {\ dagger} = - {\ hat {\ mathbf {L}}}}

y, por lo tanto, el operador de momento angular total J = L + S se vuelve negativo:

$${\ displaystyle T {\ hat {\ mathbf {J}}} T ^ {\ dagger} = - {\ hat {\ mathbf {J}}}}

Actuando en un estado propio de momento angular | j , m ⟩ , se puede demostrar que ^[1] :

$${\ displaystyle T \ left | j, m \ right \ rangle \ equiv \ left | T (j, m) \ right \ rangle = {(- 1)} ^ {jm} \ left | j, -m \ right \ sonar

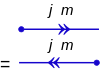
Los diagramas de tiempo invertido para kets y sujetadores son:

Tiempo invertido ket | j , m ⟩ .

Tiempo invertido sujetador ⟨ j , m | .

Es importante posicionar el vértice correctamente, ya que los operadores de tiempo de avance y de tiempo invertido se mezclarían.

Producto interno [ editar ]

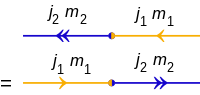
El producto interior de dos estados | j ₁ , m ₁ ⟩ y | j ₂ , m ₂ ⟩ es:

$${\ displaystyle \ langle j_ {2}, m_ {2} | j_ {1}, m_ {1} \ rangle = \ delta _ {j_ {1} j_ {2}} \ delta _ {m_ {1} m_ { 2}}}

y los diagramas son:

Producto interno de | j ₁ , m ₁ ⟩ y | j ₂ , m ₂ ⟩ , que es ⟨ j ₂ , m ₂ | j ₁ , m ₁ ⟩ .

Tiempo invertido equivalente.

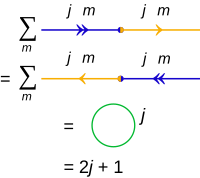
Para las sumas sobre el producto interno, también conocido en este contexto como una contracción (cf contracción del tensor ):

$${\ displaystyle \ sum _ {m} \ langle j, m | j, m \ rangle = 2j + 1}

es convencional denotar el resultado como un círculo cerrado etiquetado solo por j , no m :

Contracción interna del producto.

Productos externos [ editar ]

El producto exterior de dos estados | j ₁ , m ₁ ⟩ y | j ₂ , m ₂ ⟩ es un operador:

$${\ displaystyle \ left | j_ {2}, m_ {2} \ right \ rangle \ left \ langle j_ {1}, m_ {1} \ right |}

y los diagramas son:

Producto exterior de | j ₁ , m ₁ ⟩ y | j ₂ , m ₂ ⟩ , es decir | j ₂ , m ₂ ⟩ ⟨ j ₁ , m ₁ | .

Tiempo invertido equivalente.

Para las sumas sobre el producto externo, también conocido en este contexto como una contracción (cf contracción del tensor ):

{\ displaystyle {\ begin {alineado} \ sum _ {m} | j, m \ rangle \ langle j, m | & = \ sum _ {m} | j, -m \ rangle \ langle j, -m | \ \ & = \ sum _ {m} {(- 1)} ^ {2 (jm)} | j, -m \ rangle \ langle j, -m | \\ & = \ sum _ {m} {(- 1 )} ^ {jm} | j, -m \ rangle \ langle j, -m | {(- 1)} ^ {jm} \\ & = \ sum _ {m} T | j, m \ rangle \ langle j , m | T ^ {\ dagger} \ end {alineado}}}

donde el resultado para T | j , m ⟩ se utilizó, y el hecho de que m toma el conjunto de valores dados anteriormente. No hay diferencia entre los estados de tiempo de avance y de tiempo invertido para la contracción del producto externo, por lo que aquí comparten el mismo diagrama, representado como una línea sin dirección, nuevamente etiquetado con j solamente y no m :

Contracción externa del producto.

Productos tensores [ editar ]

El tensor del producto ⊗ de n estados | j ₁ , m ₁ ⟩ , | j ₂ , m ₂ ⟩ , ... | j _n , m _n ⟩ está escrito

{\ displaystyle {\ begin {alineado} \ left | j_ {1}, m_ {1}, j_ {2}, m_ {2}, ... j_ {n}, m_ {n} \ right \ rangle & \ equiv \ left | j_ {1}, m_ {1} \ right \ rangle \ otimes \ left | j_ {2}, m_ {2} \ right \ rangle \ otimes \ cdots \ otimes \ left | j_ {n}, m_ {n} \ right \ rangle \\ & \ equiv \ left | j_ {1}, m_ {1} \ right \ rangle \ left | j_ {2}, m_ {2} \ right \ rangle \ cdots \ left | j_ {n}, m_ {n} \ right \ rangle \ end {alineado}}}

y en forma de diagrama, cada estado separado deja o ingresa a un vértice común creando un "abanico" de flechas - n líneas unidas a un solo vértice.

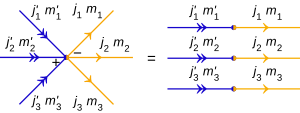
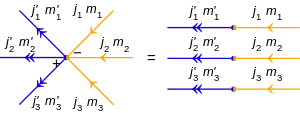
Los vértices en productos tensoriales tienen signos (a veces llamados "signos de nodo"), que indican el orden de los estados multiplicados por el tensor:

• un signo menos (-) indica que el orden es hacia la derecha ,$${\ displaystyle \ circlearrowright}y
• un signo más (+) para a la izquierda ,$${\ displaystyle \ circlearrowleft}.

Por supuesto, las señales no son necesarias para un solo estado, diagramáticamente una flecha en un vértice. A veces se incluyen flechas curvas con los signos para mostrar explícitamente el sentido de la multiplicación del tensor, pero generalmente solo se muestra el signo con las flechas que quedan fuera.

Tensor de producto de | j ₁ , m ₁ ⟩, | j ₂ , m ₂ ⟩ , | j ₃ , m ₃ ⟩ , es decir | j ₁ , m ₁ ⟩ | j ₂ , m ₂ ⟩ | j ₃ , m ₃ ⟩ = | j ₁ , m ₁ , j ₂ ,m ₂ , j ₃ , m ₃ ⟩ . Del mismo modo para más de tres momentos angulares.

Tiempo invertido equivalente.

Para el producto interno de dos estados del producto tensorial:

{\ displaystyle {\ begin {alineado} & \ left \ langle j '_ {n}, m' _ {n}, ..., j '_ {2}, m' _ {2}, j '_ { 1}, m '_ {1} | j_ {1}, m_ {1}, j_ {2}, m_ {2}, ... j_ {n}, m_ {n} \ right \ rangle \\ = & \ langle j '_ {n}, m' _ {n} | ... \ langle j '_ {2}, m' _ {2} | \ langle j '_ {1}, m' _ {1} || j_ {1}, m_ {1} \ rangle | j_ {2}, m_ {2} \ rangle ... | j_ {n}, m_ {n} \ rangle \\ = & \ prod _ {k = 1} ^ {n} \ left \ langle j '_ {k}, m' _ {k} | j_ {k}, m_ {k} \ right \ rangle \ end {alineado}}}

Hay n lotes de flechas de producto interno:

Producto interno de | j ' ₁ , m ' ₁ , j ' ₂ , m ' ₂ , j ' ₃ , m ' ₃ ⟩ y | j ₁ , m ₁ , j ₂ , m ₂ , j ₃ , m ₃ ⟩ , que es ⟨ j ' ₃ , m ' ₃ , j′ ₂ , m ′ ₂ , j ′ ₁ , m ′ ₁ | j ₁ , m ₁ , j ₂ , m ₂ , j ₃ , m ₃ ⟩. Del mismo modo para más de tres pares de momenta angular.

Tiempo invertido equivalente.

Ejemplos y aplicaciones [ editar ]

• Los diagramas son adecuados para los coeficientes de Clebsch-Gordan .
• Cálculos con sistemas cuánticos reales, tales como átomos multielectrónicos y sistemas moleculares .

Diagrama para un símbolo 6-j ,{\ displaystyle {\ begin {Bmatrix} j_ {1} & j_ {2} & j_ {3} \\ j_ {4} & j_ {5} & j_ {6} \ end {Bmatrix}}}.

Diagrama para un símbolo 9-j ,{\ displaystyle {\ begin {Bmatrix} j_ {1} & j_ {2} & j_ {3} \\ j_ {4} & j_ {5} & j_ {6} \\ j_ {7} & j_ {8} & j_ {9} \ fin {Bmatrix}}}.