MECÁNICA CUÁNTICA

Un láser atómico es un estado coherente de átomos en propagación. Se crean a partir de un condensado de átomos Bose-Einstein que se emiten acoplados mediante diversas técnicas. Al igual que un láser óptico , un láser atómico es un coherenteHaz que se comporta como una ola. Ha habido algún argumento de que el término "láser atómico" es engañoso. De hecho, "láser" significa "Amplificación de luz por emisión estimulada de radiación", que no está particularmente relacionada con el objeto físico llamado láser atómico, y tal vez describe con mayor precisión el condensado de Bose-Einstein (BEC). La terminología más utilizada en la comunidad actual es distinguir entre el BEC, que se obtiene típicamente por evaporación en una trampa conservadora, del láser atómico en sí, que es una onda atómica de propagación obtenida por extracción de un BEC previamente realizado. Algunas investigaciones experimentales en curso intentan obtener directamente un láser atómico a partir de un haz "caliente" de átomos sin hacer un BEC atrapado primero.

Introducción [ editar ]

El primer láser atómico pulsado fue demostrado en el MIT por el profesor Wolfgang Ketterle et al. en noviembre de 1996. ^[2] Ketterle usó un isótopo de sodio y usó un campo magnético oscilante como su técnica de acoplamiento de salida, lo que permitió que la gravedad sacara piezas parciales parecidas a un grifo de goteo (vea la película en Enlaces externos).

Desde la creación del primer láser atómico, ha habido un aumento en la recreación de los láseres atómicos junto con diferentes técnicas para el acoplamiento de salida y en la investigación general. La etapa de desarrollo actual del láser atómico es análoga a la del láser óptico durante su descubrimiento en la década de 1960. A tal efecto, el equipo y las técnicas se encuentran en sus primeras fases de desarrollo y aún están estrictamente en el dominio de los laboratorios de investigación.

Física [ editar ]

La física de un láser atómico es similar a la de un láser óptico. Las principales diferencias entre un láser óptico y un láser atómico son que los átomos interactúan entre sí, no pueden crearse como los fotones, y poseen masa, mientras que los fotones no (los átomos se propagan a una velocidad inferior a la de la luz). ^[3] La interacción de van der Waals de los átomos con las superficies dificulta la creación de espejos atómicos , típicos de los láseres convencionales.

Theodor Hänsch , Immanuel Bloch y Tilman Esslinger demostraron por primera vez un láser atómico de funcionamiento pseudo-continuo en el Max Planck Institute for Quantum Optics en Munich. ^[4] Producen un haz continuo bien controlado que se extiende hasta 100 ms, mientras que su predecesor produjo solo pulsos cortos de átomos. Sin embargo, esto no constituye un láser de átomo continuo ya que la reposición del BEC empobrecido dura aproximadamente 100 veces más que la duración de la emisión en sí (es decir, el ciclo de trabajo es 1/100).

Aplicaciones [ editar ]

Esta sección necesita expansión. Puedes ayudar añadiéndolo . ( Junio ​​2008 )

Este artículo necesita citas adicionales para su verificación . Por favor, ayudar a mejorar este artículo mediante la adición de citas de fuentes confiables . El material sin fuente puede ser desafiado y eliminado.  Encuentre fuentes:  "Atom laser"  -  noticias  · periódicos  · libros  · erudito  · JSTOR (noviembre de 2012 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Los láseres atómicos son críticos para la holografía atómica . Similar a la holografía convencional , la holografía de átomos usa la difracción de los átomos. La longitud de onda de De Broglie de los átomos es mucho más pequeña que la longitud de onda de la luz, por lo que los láseres de átomos pueden crear imágenes holográficas de resolución mucho más alta. La holografía atómica se puede utilizar para proyectar patrones de circuitos integrados complejos, solo unos pocos nanómetros en escala, sobre semiconductores. Otra aplicación, que también podría beneficiarse de los láseres atómicos, es la interferometría atómica.. En un interferómetro atómico, un paquete de ondas atómicas se divide coherentemente en dos paquetes de ondas que siguen diferentes caminos antes de recombinarse. Los interferómetros atómicos, que pueden ser más sensibles que los interferómetros ópticos, podrían usarse para probar la teoría cuántica y tienen una precisión tan alta que incluso podrían detectar cambios en el espacio-tiempo. ^[5] Esto se debe a que la longitud de onda de De Broglie de los átomos es mucho más pequeña que la longitud de onda de la luz, los átomos tienen masa y porque la estructura interna del átomo también puede ser explotada.

La transición electrónica atómica es un cambio de un electrón de un nivel de energía a otro dentro de un átomo ^[1] o átomo artificial . ^[2] Parece discontinuo cuando el electrón "salta" de un nivel de energía a otro en unos pocos nanosegundos o menos. También se conoce como transición atómica , salto cuántico o salto cuántico.

Las transiciones de electrones causan la emisión o absorción de radiación electromagnética en forma de unidades cuantificadas llamadas fotones . Sus estadísticas son de Poissonian , y el tiempo entre saltos se distribuye exponencialmente . ^[3] La constante de tiempo de amortiguación (que va desde los nanosegundoshasta unos pocos segundos) se relaciona con la ampliación natural, de presión y de campo de las líneas espectrales . Cuanto mayor sea la separación de energía de los estados entre los cuales salta el electrón, más corta será la longitud de onda del fotón emitido.

Hans Dehmelt predijo la observabilidad de los saltos cuánticos en 1975, y se observaron por primera vez utilizando iones de mercurio atrapados en el NIST en 1986.

El campo auxiliar Monte Carlo es un método que permite el cálculo, mediante el uso de técnicas de Monte Carlo , de promedios de operadores en mecánica cuántica de muchos cuerpos (Blankenbecler 1981, Ceperley 1977) o problemas clásicos (Baeurle 2004, Baeurle 2003, Baeurle 2002a) .

Procedimiento de recompensa y problema de signo numérico [ editar ]

El ingrediente distintivo del "campo auxiliar de Monte Carlo" es el hecho de que las interacciones se desacoplan mediante la aplicación de la transformación Hubbard-Stratonovich , que permite la reformulación de la teoría de muchos cuerpos en términos de una representación de campo auxiliar escalar . Esto reduce el problema de muchos cuerpos al cálculo de una suma o integral en todas las posibles configuraciones de campo auxiliar . En este sentido, hay una compensación: en lugar de tratar con un problema de muchos cuerpos muy complicado, uno se enfrenta al cálculo de un número infinito de problemas simples de campo externo.

Es aquí, como en otros métodos relacionados, donde Monte Carlo ingresa al juego con el pretexto de la importancia del muestreo : la gran suma sobre las configuraciones de campo auxiliar se realiza mediante el muestreo sobre los más importantes, con cierta probabilidad . En la física estadística clásica , esta probabilidad suele estar dada por el factor de Boltzmann (semidefinido positivo). Factores similares surgen también en las teorías cuánticas de campos; sin embargo, estos pueden tener un signo indefinido (especialmente en el caso de los fermiones) o incluso tener un valor complejo, lo que excluye su interpretación directa como probabilidades. En estos casos, uno tiene que recurrir a un procedimiento de reponderación (es decir, interpretar el valor absoluto como la probabilidad y multiplicar el signo o la fase en lo observable) para obtener una distribución de referencia estrictamente positiva adecuada para el muestreo de Monte Carlo. Sin embargo, es bien sabido que, en rangos de parámetros específicos del modelo en consideración, la naturaleza oscilatoria de la función de ponderación puede llevar a una mala convergencia estadística del procedimiento de integración numérica . El problema se conoce como el problema de signo numérico.y se puede aliviar con procedimientos de aceleración de convergencia analítica y numérica (Baeurle 2002, Baeurle 2003a).

 cruce evitado (a veces llamado cruce intencional , ^[1] no cruzado o anticrossing ) es el fenómeno donde dos valores propios de una matriz hermitiana que representan un valor observable cuántico y que dependen de N parámetros reales continuos no pueden igualarse valor ("cruz") excepto en una variedad de N -2 dimensiones. ^[2] En el caso de una molécula diatómica (con un parámetro, a saber, la longitud del enlace), esto significa que los valores propios no pueden cruzarse en absoluto. En el caso de una molécula triatómica , esto significa que los valores propios pueden coincidir solo en un punto (ver intersección cónica ).

Esto es particularmente importante en la química cuántica . En la aproximación Born-Oppenheimer , el hamiltoniano molecular electrónico está diagonalizado en un conjunto de geometrías moleculares distintas (los valores propios obtenidos son los valores de las superficies de energía potencial adiabática ). Las geometrías para las que las superficies de energía potencial evitan cruzar son el lugar donde falla la aproximación de Born – Oppenheimer.

En sistemas de dos estados [ editar ]

Emergencia [ editar ]

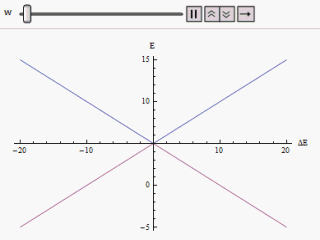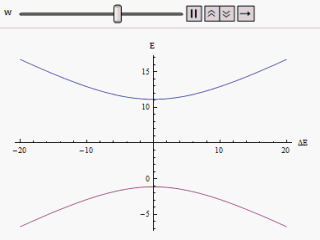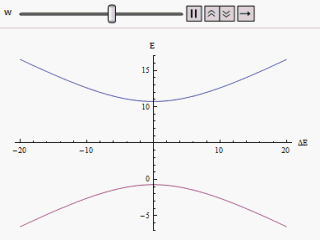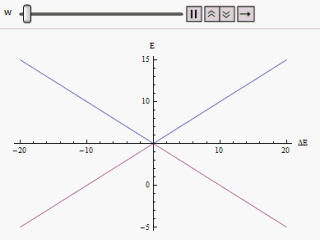
El estudio de un sistema de dos niveles es de vital importancia en la mecánica cuántica porque encarna la simplificación de muchos de los sistemas físicamente realizables. El efecto de la perturbación en un sistema hamiltoniano de dos estados se manifiesta a través de cruces evitados en la gráfica de la curva de energía individual frente a diferencia de energía de los estados propios. ^[3] El Hamiltoniano de dos estados se puede escribir como

{\ displaystyle H = {\ begin {pmatrix} E_ {1} & 0 \\ 0 & E_ {2} \ end {pmatrix}} \, \!}

Los valores propios de los cuales son $${\ displaystyle \ textstyle E_ {1}} y $${\ displaystyle \ textstyle E_ {2}}y los vectores propios ,$${\ displaystyle \ textstyle {\ begin {pmatrix} 1 \\ 0 \ end {pmatrix}}} y $${\ displaystyle \ textstyle {\ begin {pmatrix} 0 \\ 1 \ end {pmatrix}}}. Estos dos vectores propios designan los dos estados del sistema. Si el sistema está preparado en cualquiera de los estados, permanecerá en ese estado. Si$${\ displaystyle \ textstyle E_ {1}} pasa a ser igual a $${\ displaystyle E_ {2}}Habrá una doble degeneración en el hamiltoniano. En ese caso, cualquier superposición de estados propios degenerados es evidentemente otro estado propio del hamiltoniano. Por lo tanto, el sistema preparado en cualquier estado permanecerá en eso para siempre.

Cruce evitado en el sistema de dos estados. El paso del nivel de energía se evita aumentando el parámetro.$${\ displaystyle \ textstyle w (= | W |)}. En ausencia de perturbación externa, los niveles se habrían cruzado si los estados de energía originales hubieran sido degenerados, es decir,$${\ displaystyle \ textstyle \ Delta E = 0}

Sin embargo, cuando se somete a una perturbaciónexterna , los elementos de la matriz del Hamiltoniano cambian. En aras de la simplicidad, consideramos una perturbación con elementos solo diagonales. Como el hamiltoniano en general debe ser hermitiano, simplemente podemos escribir el nuevo hamiltoniano.

{\ displaystyle H ^ {'} = H + P = {\ begin {pmatrix} E_ {1} & 0 \\ 0 & E_ {2} \ end {pmatrix}} + {\ begin {pmatrix} 0 & W \\ W ^ {* } & 0 \ end {pmatrix}} = {\ begin {pmatrix} E_ {1} & W \\ W ^ {*} & E_ {2} \ end {pmatrix}} \, \!}

Donde P es la perturbación con cero diagonales. El hecho de que P es hermitiano arregla sus componentes fuera de la diagonal. Los estados propios modificados se pueden encontrar diagonalizando el hamiltoniano modificado. Resulta que los nuevos valores propios son,

$${\ displaystyle E _ {+} = {\ frac {1} {2}} (E_ {1} + E_ {2}) + {\ frac {1} {2}} {\ sqrt {(E_ {1} - E_ {2}) ^ {2} +4 | W | ^ {2}}}}

$${\ displaystyle E _ {-} = {\ frac {1} {2}} (E_ {1} + E_ {2}) - {\ frac {1} {2}} {\ sqrt {(E_ {1} - E_ {2}) ^ {2} +4 | W | ^ {2}}}}

Si se grafica una gráfica variando $${\ displaystyle \ textstyle (E_ {1} -E_ {2})} a lo largo del eje horizontal y $${\ displaystyle \ textstyle E _ {+}} o $${\ displaystyle \ textstyle E _ {-}}a lo largo de la vertical, encontramos dos ramas de una hipérbola (como se muestra en la figura). La curva se aproxima asintóticamente a los niveles de energía no perturbados originales. Al analizar las curvas, se hace evidente que incluso si los estados originales estaban degenerados (es decir,$${\ displaystyle \ textstyle E_ {1} = E_ {2}}) Los nuevos estados de energía ya no son iguales. Sin embargo, si$${\ displaystyle \ textstyle W} se pone a cero que podemos encontrar en $${\ displaystyle \ textstyle (E_ {1} -E_ {2}) = 0}, $${\ displaystyle \ textstyle E _ {+} = E _ {-}}y los niveles se cruzan. Así, con el efecto de la perturbación se evitan estos pasos a nivel.

Resonancia Quantum [ editar ]

El impacto inmediato del paso a nivel evitado en un sistema degenerado de dos estados es la aparición de un estado propio de energía disminuido. La reducción efectiva de la energía siempre corresponde al aumento de la estabilidad (ver: Minimización de la energía ) La resonancia de enlace en moléculas orgánicas ejemplifica la aparición de tales cruces evitados. Para describir estos casos, podemos notar que los elementos no diagonales en un Hamiltoniano antiguo diagonal no solo modifican los valores propios de la energía sino que también superponen los estados propios antiguos en los nuevos. ^[4] Estos efectos son más prominentes si el hamiltoniano original tuvo degeneración. Esta superposición de estados propios para lograr una mayor estabilidad es precisamente el fenómeno de la resonancia del enlace químico.

Nuestro tratamiento anterior comenzó denotando los vectores propios $${\ displaystyle \ textstyle {\ begin {pmatrix} 1 \\ 0 \ end {pmatrix}}} y $${\ displaystyle \ textstyle {\ begin {pmatrix} 0 \\ 1 \ end {pmatrix}}} como la representación matricial de estados propios $${\ displaystyle \ textstyle | \ psi _ {1} \ rangle} y $${\ displaystyle \ textstyle | \ psi _ {2} \ rangle}de un sistema de dos estados. Usando la notación bra-ket los elementos de la matriz de$${\ displaystyle H ^ {'}} son en realidad los términos

$${\ displaystyle H_ {ij} ^ {'} = \ langle \ psi _ {i} | H ^ {'} | \ psi _ {j} \ rangle} con $${\ displaystyle i, j \ in \ left \ {{1,2} \ right \}}

dónde $${\ displaystyle H_ {11} ^ {'} = H_ {22} ^ {'} = E} Debido a la degeneración del Hamiltoniano imperturbado y las perturbaciones fuera de la diagonal son $${\ displaystyle H_ {12} ^ {'} = W} y $${\ displaystyle H_ {21} ^ {'} = W ^ {*}}.

Los nuevos estados propios $${\ displaystyle \ textstyle | \ psi _ {+} \ rangle} y $${\ displaystyle \ textstyle | \ psi _ {-} \ rangle} Se puede encontrar resolviendo las ecuaciones de valores propios. $${\ displaystyle H ^ {'} | \ psi _ {+} \ rangle = E _ {+} | \ psi _ {+} \ rangle} y $${\ displaystyle H ^ {'} | \ psi _ {-} \ rangle = E _ {-} | \ psi _ {-} \ rangle}. De simples cálculos se puede demostrar que

$${\ displaystyle | \ psi _ {+} \ rangle = {\ frac {1} {\ sqrt {2}}} {\ begin {pmatrix} e ^ {i \ phi} \\ 1 \ end {pmatrix}} = {\ frac {1} {\ sqrt {2}}} (e ^ {i \ phi} | \ psi _ {1} \ rangle + | \ psi _ {2} \ rangle)} y

$${\ displaystyle | \ psi _ {-} \ rangle = {\ frac {1} {\ sqrt {2}}} {\ begin {pmatrix} -e ^ {i \ phi} \\ 1 \ end {pmatrix}} = {\ frac {1} {\ sqrt {2}}} (- e ^ {i \ phi} | \ psi _ {1} \ rangle + | \ psi _ {2} \ rangle)} dónde $${\ displaystyle e ^ {i \ phi} = W / | W |}

Es evidente que los dos estados propios nuevos son superposición de los estados propios degenerados originales y uno de los valores propios (aquí $${\ displaystyle E _ {-}}) es menor que la eigenenergía original no perturbada. Así que el sistema estable correspondiente mezclará naturalmente los estados propios no perturbados anteriores para minimizar su energía. En el ejemplo del benceno, las evidencias experimentales de las estructuras de enlace probables dan lugar a dos estados propios diferentes,$${\ displaystyle \ textstyle | \ psi _ {1} \ rangle} y $${\ displaystyle \ textstyle | \ psi _ {2} \ rangle}. La simetría de estas dos estructuras obliga a que$${\ displaystyle \ langle \ psi _ {1} | H | \ psi _ {1} \ rangle = \ langle \ psi _ {2} | H | \ psi _ {2} \ rangle = E}.

Sin embargo, resulta que el Hamiltoniano de dos estados $${\ displaystyle H}El benceno no es diagonal. Los elementos fuera de la diagonal resultan en una disminución de energía y la molécula de benceno se estabiliza en una estructura que es una superposición de estas simétricas con energía.{\ displaystyle E _ {-} . ^[5] Para cualquier sistema general de dos estados que se evite el paso a nivel, se repelen los estados propios$${\ displaystyle | \ psi _ {+} \ rangle} y $${\ displaystyle | \ psi _ {-} \ rangle} de tal manera que requiere más energía para que el sistema logre la configuración de energía más alta.

En general evitó cruzar el teorema [ editar ]

Sin embargo, la ilustración anterior del cruce evitado es un caso muy específico. Desde un punto de vista generalizado, el fenómeno de cruce evitado está controlado por los parámetros detrás de la perturbación. Para la perturbación más general.{\ displaystyle \ textstyle P = {\ begin {pmatrix} W_ {1} & W \\ W & W_ {2} \ end {pmatrix}}}Afectando un subespacio bidimensional del hamiltoniano.$${\ displaystyle H}, podemos escribir la matriz hamiltoniana efectiva en ese subespacio como

{\ displaystyle {\ begin {pmatrix} E_ {1} & 0 \\ 0 & E_ {2} \ end {pmatrix}} + {\ begin {pmatrix} W_ {1} & W \\ W & W_ {2} \ end {pmatrix}} = {\ begin {pmatrix} E_ {1} + W_ {1} & W \\ W & E_ {2} + W_ {2}. \ end {pmatrix}}.}

Aquí, los elementos de los vectores de estado se eligieron para ser reales de modo que todos los elementos de la matriz se vuelvan reales. ^[6] Ahora, los valores propios del sistema para este subespacio están dados por

$${\ displaystyle E _ {\ pm} = {\ frac {1} {2}} (E_ {1} + E_ {2} + W_ {1} + W_ {2}) \ pm {\ frac {1} {2 }} {\ sqrt {(E_ {1} -E_ {2} + W_ {1} -W_ {2}) ^ {2} + 4W ^ {2}}}}

Los términos debajo de la raíz cuadrada son números reales cuadrados. Así que para que estos dos niveles se crucen requerimos simultáneamente

$${\ displaystyle (E_ {1} -E_ {2} + W_ {1} -W_ {2}) = 0}

$${\ displaystyle W = 0.}

Ahora si la perturbación $${\ displaystyle P} tiene $${\ displaystyle k} parámetros $${\ displaystyle {\ alpha _ {1}, \ alpha _ {2}, \ alpha _ {3} ..... \ alpha _ {k}}} En general, podemos variar estos números para satisfacer estas dos ecuaciones.

$${\ displaystyle (E_ {1} -E_ {2} + W_ {1} -W_ {2}) = F_ {1} (\ alpha _ {1}, \ alpha _ {2}, \ alpha _ {3} ..... \ alpha _ {k}) = 0}

$${\ displaystyle W = F_ {2} (\ alpha _ {1}, \ alpha _ {2}, \ alpha _ {3} ..... \ alpha _ {k}) = 0.}

Si elegimos los valores de $${\ displaystyle \ alpha _ {1}} a $${\ displaystyle \ alpha _ {k-1}}Entonces, las dos ecuaciones anteriores tienen un solo parámetro libre. En general no es posible encontrar uno.$${\ displaystyle \ alpha _ {k}}de tal manera que se satisfacen ambas ecuaciones. Sin embargo, si permitimos que otro parámetro esté libre, estas dos ecuaciones ahora serán controladas por los mismos dos parámetros

$${\ displaystyle F_ {1} (\ alpha _ {k-1}, \ alpha _ {k}) | _ {\ alpha _ {1}, \ alpha _ {2}, ..., \ alpha _ {k -2} \, corregido} = 0}

$${\ displaystyle F_ {2} (\ alpha _ {k-1}, \ alpha _ {k}) | _ {\ alpha _ {1}, \ alpha _ {2}, ..., \ alpha _ {k -2} \, corregido} = 0.}

Y generalmente habrá dos valores de ellos para los cuales se satisfarán simultáneamente las ecuaciones. Asi que con$${\ displaystyle k} parámetros distintos $${\ displaystyle k-2} Los parámetros siempre se pueden elegir arbitrariamente y aún podemos encontrar dos tales $${\ displaystyle \ alpha _ {k}}s tal que habría cruce de valores propios de energía. En otras palabras, los valores de$${\ displaystyle E _ {+}}y $${\ displaystyle E _ {-}} sería lo mismo para $${\ displaystyle k-2}coordenadas que varían libremente (mientras que el resto de las dos coordenadas se fijan a partir de las ecuaciones de condición). Geométricamente, las ecuaciones de valores propios describen una superficie en$${\ displaystyle k} espacio dimensional.

$${\ displaystyle E _ {\ pm} = E _ {\ pm} (\ alpha _ {1}, \ alpha _ {2}, \ alpha _ {3} ..... \ alpha _ {k}).}

Dado que su intersección está parametrizada por$${\ displaystyle k-2} coordenadas, podemos afirmar formalmente que para $${\ displaystyle k}parámetros reales continuos que controlan el Hamiltoniano perturbado, los niveles (o superficies) solo pueden cruzarse en una variedad de dimensiones$${\ displaystyle k-2}. ^[7] Sin embargo, la simetría del hamiltoniano tiene un papel que desempeñar en la dimensionalidad. Si el hamiltoniano original tiene estados asimétricos,$${\ displaystyle \ langle \ psi _ {1} | P | \ psi _ {2} \ rangle \ neq \ langle \ psi _ {2} | P | \ psi _ {1} \ rangle}, los términos fuera de la diagonal se desvanecen automáticamente para asegurar la hermiticidad. Esto nos permite deshacernos de la ecuación.$${\ displaystyle W = 0}. Ahora, a partir de argumentos similares a los planteados anteriormente, es claro que para un hamiltoniano asimétrico, la intersección de las superficies de energía tiene lugar en una variedad de dimensiones.$${\ displaystyle k-1}. ^[8]

En las moléculas poliatómicas [ editar ]

En las moléculas poliatómicas, hay varios parámetros que determinan el hamiltoniano del sistema. Las distancias mutuas entre los átomos son un conjunto de parámetros. Si los dos átomos de una molécula diatómica son iguales, la simetría sugiere que las diferentes configuraciones que mantienen su distancia mutua fija resultarán en los mismos estados electrónicos. ^{[ aclaración necesaria ]} Así que es la distancia relativa$${\ displaystyle r}que actúa como un parámetro para las dos ecuaciones que prometen ^{[paso de aclaración ]} paso a nivel. Por lo tanto, debido al teorema de cruce evitado en general, no podemos tener pasos a nivel entre dos estados electrónicos de la misma simetría. ^[9] Pero en las moléculas poliatómicas el número de distancias mutuas independientes de los núcleos es mayor. Para una molécula atómica N, el número de separación mutua independiente es$${\ displaystyle \ textstyle S = 3N-6} (para $${\ displaystyle \ textstyle N \ geq 3}). Cada uno de ellos actúa como un parámetro para el hamiltoniano total. Como siempre tenemos un mínimo de tres parámetros independientes, el paso a nivel no se evita totalmente en estas moléculas.