La ley de Chladni , llamada así por Ernst Chladni , relaciona la frecuencia de los modos de vibración para superficies circulares planas con un centro fijo en función de los números m de los nodos diametral (lineal) yn de los nodos radial (circular). Se establece como la ecuación.
Para placas circulares planas, p es aproximadamente 2, pero la ley de Chladni también se puede usar para describir las vibraciones de los platillos , campanillas y campanas de las iglesias, en cuyo caso p puede variar de 1.4 a 2.4. [2] De hecho, p puede incluso variar para un solo objeto, dependiendo de qué familia de modos se esté examinando.
El límite clásico o el límite de correspondencia es la capacidad de una teoría física para aproximarse o "recuperar" la mecánica clásica cuando se considera sobre valores especiales de sus parámetros. [1] El límite clásico se usa con teorías físicas que predicen el comportamiento no clásico.
La teoría cuántica [ editar ]
Un postulado heurístico llamado principio de correspondencia fue introducido en la teoría cuántica por Niels Bohr: en efecto, establece que algún tipo de argumento de continuidad debe aplicarse al límite clásico de los sistemas cuánticos, ya que el valor de la constante de Planck normalizada por la acción de estos sistemas se vuelve muy importante. pequeña. A menudo, esto se aborda a través de técnicas "cuasi-clásicas" (cf. aproximación WKB ). [2]
Más rigurosamente, [3] la operación matemática involucrada en los límites clásicos es una contracción grupal , que se aproxima a los sistemas físicos donde la acción relevante es mucho más grande que la constante de Planck ħ , por lo que el "parámetro de deformación" ħ / S puede tomarse efectivamente como cero ( cf. Cuantificación de Weyl .) Por lo tanto, típicamente, los conmutadores cuánticos (equivalentemente, los corchetes Moyal ) se reducen a los corchetes de Poisson , [4] en una contracción grupal .
En la mecánica cuántica , debido al principio de incertidumbre de Heisenberg , un electrón nunca puede estar en reposo; siempre debe tener una energía cinética no nula , un resultado que no se encuentra en la mecánica clásica. Por ejemplo, si consideramos algo muy grande en relación con un electrón, como una pelota de béisbol, el principio de incertidumbre predice que realmente no puede tener cero energía cinética, pero la incertidumbre en la energía cinética es tan pequeña que la pelota de béisbol puede parecer efectivamente descansar. , y por lo tanto parece obedecer a la mecánica clásica. En general, si en la mecánica cuántica se consideran las energías grandes y los objetos grandes (en relación con el tamaño y los niveles de energía de un electrón), el resultado parecerá obedecer a la mecánica clásica. Lo tipiconúmeros de ocupación involucrados son enormes: un oscilador armónico macroscópica con ω = 2 Hz, m = 10 g, y máximo de amplitud x 0 = 10 cm, tiene S ≈ E / ω ≈ mωx 2
0 /2 ≈ 10 -4 kg · m 2 / s = ħn , de modo que n ≃ 10 30 . Además ver estados coherentes . Sin embargo, es menos claro cómo se aplica el límite clásico a los sistemas caóticos, un campo conocido como caos cuántico .
0 /2 ≈ 10 -4 kg · m 2 / s = ħn , de modo que n ≃ 10 30 . Además ver estados coherentes . Sin embargo, es menos claro cómo se aplica el límite clásico a los sistemas caóticos, un campo conocido como caos cuántico .
La mecánica cuántica y la mecánica clásica suelen tratarse con formalismos completamente diferentes: la teoría cuántica que utiliza el espacio de Hilbert y la mecánica clásica mediante una representación en el espacio de fase . Uno puede llevar a los dos a un marco matemático común de varias maneras. En la formulación en el espacio de fases de la mecánica cuántica, que es de naturaleza estadística, se realizan conexiones lógicas entre la mecánica cuántica y la mecánica estadística clásica, lo que permite comparaciones naturales entre ellas. [5] [6]
En un documento fundamental (1933), Dirac [7] explicó cómo la mecánica clásica es un fenómeno emergente de la mecánica cuántica: la interferencia destructiva entre los caminos con la no extremal macroscópica acciones S » ħ arrasar con las contribuciones de amplitud en la integral de caminos introdujo, dejando el extremal La clase de acción S , por lo tanto, el camino de acción clásico como la contribución dominante, una observación más elaborada por Feynman en su disertación de doctorado de 1942. [8] (Ver también decoherencia cuántica ).
Evolución temporal de los valores esperados [ editar ]
Una forma sencilla de comparar la mecánica clásica con la mecánica cuántica es considerar la evolución temporal de la posición esperada y el impulso esperado , que luego puede compararse con la evolución temporal de la posición ordinaria y el impulso en la mecánica clásica. Los valores de expectativa cuántica satisfacen el teorema de Ehrenfest . Para una partícula cuántica unidimensional moviéndose en un potencial, el teorema de Ehrenfest dice [9]
Aunque la primera de estas ecuaciones es consistente con la mecánica clásica, la segunda no lo es: si el par para satisfacer la segunda ley de Newton, el lado derecho de la segunda ecuación habría leído
- .
Pero en la mayoría de los casos,
- .
Si por ejemplo, el potencial es cúbico, entonces es cuadrático, en cuyo caso estamos hablando de la distinción entre y , que difieren por .
Se produce una excepción en caso de que las ecuaciones clásicas de movimiento sean lineales, es decir, cuando es cuadrático y es lineal En ese caso especial, y de acuerdo En particular, para una partícula libre o un oscilador armónico cuántico, la posición esperada y el impulso esperado siguen exactamente las soluciones de las ecuaciones de Newton.
Para los sistemas generales, lo mejor que podemos esperar es que la posición y el impulso esperados sigan aproximadamente las trayectorias clásicas. Si la función de onda está altamente concentrada alrededor de un punto., entonces y será casi igual, ya que ambos serán aproximadamente iguales a. En ese caso, la posición esperada y el impulso esperado permanecerán muy cerca de las trayectorias clásicas, al menos mientras la función de onda permanezca altamente localizada en la posición. [10]
Ahora, si el estado inicial está muy localizado en posición, estará muy extendido en el impulso, y por lo tanto, esperamos que la función de onda se extienda rápidamente, y la conexión con las trayectorias clásicas se pierda. Sin embargo, cuando la constante de Planck es pequeña, es posible tener un estado que esté bien localizado tanto en la posición como en el momento. La pequeña incertidumbre en el momento garantiza que la partícula permanezca bien localizada en la posición durante mucho tiempo, de modo que la posición y el impulso esperados continúen siguiendo de cerca las trayectorias clásicas durante mucho tiempo.
Relatividad y otras deformaciones [ editar ]
Otras deformaciones familiares en la física implican:
- La deformación de la mecánica newtoniana clásica en relativista ( relatividad especial ), con parámetro de deformación v / c ; el límite clásico implica velocidades pequeñas, por lo que v / c → 0, y los sistemas parecen obedecer a la mecánica newtoniana.
- De manera similar, para la deformación de la gravedad newtoniana en la relatividad general , con el parámetro de deformación Schwarzschild-radio / caracter-dimensión, encontramos que los objetos parecen obedecer una vez más a la mecánica clásica (espacio plano), cuando la masa de un objeto es el cuadrado del Planck. la longitud es mucho más pequeña que su tamaño y el tamaño del problema abordado.
- La óptica de onda también podría considerarse como una deformación de la óptica de rayos para el parámetro de deformación λ / a .
- Del mismo modo, la termodinámica se deforma para la mecánica estadística con el parámetro de deformación de 1 / N .
los coeficientes de Clebsch-Gordan son los coeficientes de expansión de los estados propios del momento angular total en una base de producto tensor no acoplado . Matemáticamente, especifican la descomposición del producto tensorial de dos representaciones irreducibles en una suma directa de representaciones irreducibles, donde el tipo y las multiplicidades de estas representaciones irreducibles se conocen de manera abstracta. El nombre deriva de los matemáticos alemanes Alfred Clebsch (1833–1872) y Paul Gordan (1837–1912), que encontraron un problema equivalente en la teoría invariante.
La generalización a los coeficientes SU (3) de Clebsch-Gordan es útil debido a su utilidad para caracterizar las desintegraciones hadrónicas , donde existe una simetría de sabor SU (3) (la Óctuple Vía (física) ) que conecta los tres quarks de luz : arriba , abajo , y extraño .
Grupos [ editar ]
Un grupo es una estructura matemática (generalmente denotada en la forma consiste en un conjunto G y una operación binaria (*) (a menudo llamada 'multiplicación'), que satisface las siguientes propiedades:
- Cierre : Para cada par de elementos x e y en G , el producto También está en G (en símbolos, por cada dos elementos también está en
- Asociatividad : Por cada x e y y z en G , ambos y Resultado con el mismo elemento en G (en símbolos, para cada y ).
- Existencia de identidad : debe haber un elemento (por ejemplo, e ) en G tal que produzca cualquier elemento de G con e sin hacer ningún cambio en el elemento (en símbolos, para cada ).
- Existencia de inversa : Para cada elemento ( x ) en G , tiene que ser un elemento y en G tal que el producto de x y y es el elemento de identidad e (en símbolos, para cada hay un tal que para cada;).
- Conmutativo : Además de los cuatro anteriores, si sucede que, , entonces el grupo se llama un grupo abeliano . De lo contrario se llama un grupo no abeliano.
Grupo de simetría [ editar ]
En álgebra abstracta, el grupo de simetría de un objeto (imagen, señal, etc.) es el grupo de todas las isometríasen las que el objeto es invariante con la composición como operación. Es un subgrupo del grupo de isometría del espacio en cuestión. [1] En mecánica cuántica, todas las transformaciones de un sistema que dejan el Hamiltoniano sin cambios comprenden el grupo de simetría del Hamiltoniano. La operación de grupo es un operador de multiplicación binaria.
El operador de simetría conmuta con el hamiltoniano, es decir,
- o,
- así
El conjunto de todos comprende un grupo, con el elemento de identidad siendo - Lo que no corresponde a ninguna transformación en el hamiltoniano. Todas las transformaciones tienen un inverso. Así, estos forman un grupo [2]
El grupo SU (3) [ editar ]
El grupo unitario especial SU es el grupo de matrices unitarias cuyo determinante es igual a 1. [3] Este conjunto está cerrado bajo la multiplicación de matrices. Todas las transformaciones caracterizadas por el grupo unitario especial no modifican las normas. La simetría SU (3) aparece en la cromodinámica cuántica , y, como ya se indicó en la simetría del sabor de quark ligero, se denominó la Óctuple Vía (física) . Los quarks poseen números cuánticos de color y forman la representación fundamental (triplete) de un grupo SU (3) .
El grupo SU (3) es un subgrupo del grupo U (3) , el grupo de todas las matrices unitarias 3 × 3. La condición de unidad impone nueve relaciones de restricción en el total de 18 grados de libertad de una matriz compleja de 3 × 3. Por lo tanto, la dimensión del grupo U (3) es 9. Además, al multiplicar una U por una fase, e iφ deja la norma invariante. Por lo tanto, U (3) se puede descomponer en un producto directo de U (1) ⊗SU (3) . Debido a esta restricción adicional, SU (3) tiene dimensión 8.
Generadores del álgebra de Lie [ editar ]
Cada matriz unitaria U se puede escribir en la forma
dónde Son las 8 matrices linealmente independientes que forman la base del álgebra de Lie de SU (3) , en la representación de la tripeta. La condición determinante de la unidad requiere la Las matrices no tienen rastro, ya que
- .
Una base explícita en la representación fundamental, 3 , puede construirse en analogía con el álgebra matricial de Pauli de los operadores de espín. Se compone de las matrices de Gell-Mann ,
Estos son los generadores del grupo SU (3) en la representación de triplete, y se normalizan como
Las constantes de la estructura de álgebra de Lie del grupo están dadas por los conmutadores de
dónde son las constantes de estructura completamente antisimétricas y son análogas al símbolo de Levi-Civita de SU (2) .
En general, desaparecen, a menos que contengan un número impar de índices del conjunto {2,5,7}, correspondiente a la antisimétrica λ s. Nota.
Además,
dónde Son las constantes de coeficientes completamente simétricas. Se desvanecen si el número de índices del conjunto {2,5,7} es impar.
Base estandar [ editar ]
Una base estándar ligeramente diferente normalizada consiste en los operadores F-spin , que se definen comopara el 3 , y se utilizan para aplicar a cualquier representación de este álgebra .
La base de Cartan-Weyl del álgebra de Lie de SU (3) se obtiene mediante otro cambio de base, donde se define, [4]
Debido a los factores de i en estas fórmulas, esto es técnicamente una base para la complejización del álgebra de su (3) Lie, es decir, sl (3, C ). La base anterior es esencialmente la misma utilizada en el libro de Hall. [5]
Álgebra de conmutación de los generadores [ editar ]
La forma estándar de los generadores del grupo SU (3) satisface las relaciones de conmutación que se indican a continuación.
Todas las demás relaciones de conmutación se derivan de la conjugación hermitiana de estos operadores.
Estas relaciones de conmutación se pueden utilizar para construir las representaciones irreductibles del grupoSU (3) .
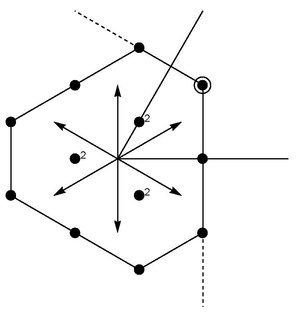
Las representaciones del grupo se encuentran en el plano bidimensional I 3 - Y. Aquí,representa el componente z de Isospin yes el Hypercharge , y comprenden la subalgebra de Cartan (abeliana) del álgebra de Lie completa. El número máximo de generadores que se conmutan mutuamente en un álgebra de Lie se denomina su rango : SU (3) tiene el rango 2. Los 6 generadores restantes, los operadores de escalera, corresponden a las 6 raíces dispuestas en la red hexagonal bidimensional de la figura. .
Operadores de Casimir [ editar ]
El operador de Casimir es un operador que conmuta con todos los generadores del grupo Lie. En el caso de SU (2) , el operador cuadrático J 2 es el único operador independiente de este tipo.
En el caso del grupo SU (3) , por el contrario, se pueden construir dos operadores Casimir independientes, uno cuadrático y otro cúbico: son, [6]
Estos operadores de Casimir sirven para etiquetar las representaciones irreductibles del álgebra SU del grupo de Lie (3) , porque todos los estados en una representación dada asumen el mismo valor para cada operador de Casimir, que sirve como identidad en un espacio con la dimensión de esa representación. Esto se debe a que los estados en una representación dada están conectados por la acción de los generadores del álgebra de Lie, y todos los generadores conmutan con los operadores de Casimir.
Por ejemplo, para la representación de triplete, D (1,0) , el valor propio de es 4/3, y de , 10/9.
Más generalmente, a partir de la fórmula de Freudenthal , para D genérico (p, q) , el valor propio [7] de es .
El valor propio ("coeficiente de anomalía") de es [8] Es una función impar bajo el intercambio p ↔ q . En consecuencia, desaparece para representaciones reales p = q , como el adjunto, D (1,1) , es decir, ambos Y las anomalías se desvanecen por ello.
Representaciones del grupo SU (3) [ editar ]
Las representaciones irreducibles de SU (3) se analizan en varios lugares, incluido el libro de Hall. [9] Dado que el grupo SU (3) está simplemente conectado, [10] las representaciones están en correspondencia uno a uno con las representaciones de su álgebra de Lie [11] su (3), o la complejización [12] de su Lie algebra, sl (3, C ).
Las representaciones se etiquetan como D (p, q), siendo p y q enteros no negativos, donde en términos físicos, pes el número de quarks y q es el número de antiquarks. Matemáticamente, la representación D (p, q) se puede construir mediante la tensoría de p copias de la representación tridimensional estándar y q copias del dual de la representación estándar, y luego extraer un subespacio invariante irreductible. [13] (Consulte también la sección de cuadros jóvenes a continuación: p es el número de columnas de un solo cuadro, "quarks" yqel número de columnas de doble caja, "antiquarks"). Otra forma de pensar acerca de los parámetros p y q es como los valores propios máximos de las matrices diagonales.
- .
(Los elementos y Son combinaciones lineales de los elementos. y , pero normalizado para que los valores propios de y son enteros.) Esto debe compararse con la teoría de representación de SU (2) , donde las representaciones irreductibles están marcadas por el valor propio máximo de un solo elemento, h .
Las representaciones tienen dimensión [14].
Un múltiplet SU (3) se puede especificar completamente con cinco etiquetas, dos de las cuales, los valores propios de los dos Casimir, son comunes a todos los miembros del multiplete. Esto generaliza las meras dos etiquetas para los multiplets SU (2) , a saber, los valores propios de su Casimir cuadrático y de I 3 .
Ya que , podemos etiquetar diferentes estados por los valores propios de y operadores, , para un valor propio dado de la isospina Casimir. La acción de los operadores en estos estados es, [15]
Aquí,
y
Todos los demás estados de la representación pueden construirse mediante la aplicación sucesiva de los operadores de escalera. y e identificando los estados base que son aniquilados por la acción de los operadores que bajan. Estos operadores se encuentran en los vértices y el centro de un hexágono.
Coeficiente de Clebsch-Gordan para SU (3) [ editar ]
La representación del producto de dos representaciones irreductibles. y Es generalmente reducible. Simbólicamente,
dónde es un entero
Por ejemplo, dos octetos (adjuntos) se componen de
es decir, su producto se reduce a un icosaseptet ( 27 ), decuplet, dos octetos, un antidecuplet y un singlete, 64 estados en total.
La serie de la derecha se llama la serie Clebsch-Gordan. Implica que la representación. aparece tiempos en la reducción de este producto directo de con .
Ahora se necesita un conjunto completo de operadores para especificar de manera única los estados de cada representación irreducible dentro de la que se acaba de reducir. El conjunto completo de operadores de conmutación (CSCO) en el caso de la representación irreducible. es
dónde
- .
Los estados de la representación directa anterior del producto están así completamente representados por el conjunto de operadores
donde el número entre paréntesis designa la representación en la que actúa el operador.
Se puede encontrar un conjunto alternativo de operadores de conmutación para la representación directa del producto, si se considera el siguiente conjunto de operadores, [16]
Así, el conjunto de operadores conmutadores incluye
Este es un conjunto de nueve operadores solamente. Pero el conjunto debe contener diez operadores para definir de forma única todos los estados de la representación directa del producto. Para encontrar el último operador Γ , uno debe mirar fuera del grupo. Es necesario distinguir diferentespara valores similares de P y Q .
Por lo tanto, cualquier estado en la representación directa del producto puede ser representado por el ket,
También utilizando el segundo conjunto completo de operador de conmutación, podemos definir los estados en la representación directa del producto como
Podemos dejar caer el del estado y etiquetar los estados como
utilizando los operadores del primer set, y,
Utilizando los operadores del segundo set.
Ambos estados abarcan la representación directa del producto y cualquier estado en la representación se puede etiquetar mediante la elección adecuada de los valores propios.
Usando la relación de completitud,
Aquí, los coeficientes
Son los coeficientes de Clebsch-Gordan.
Una notación diferente [ editar ]
Para evitar confusiones, los valores propios. pueden ser denotados simultáneamente por μ y los valores propiosson denotados simultáneamente por v . Entonces el estado propio de la representación directa del productopuede ser denotado por [16]
dónde son los valores propios de y son los valores propios de denotado simultáneamente. Aquí, la cantidad expresada por el paréntesis es el símbolo Wigner 3-j .
Además, son considerados como los estados base de y son los estados base de . tambiénSon los estados base de la representación del producto. aquí representa los valores propios combinados y respectivamente.
Así las transformaciones unitarias que conectan las dos bases son
Esta es una notación comparativamente compacta. Aquí,
Son los coeficientes de Clebsch-Gordan.
Relaciones de ortogonalidad [ editar ]
Los coeficientes de Clebsch-Gordan forman una matriz ortogonal real. Por lo tanto,
Además, siguen las siguientes relaciones de ortogonalidad,
Propiedades de simetría [ editar ]
Si una representación irreducible. apperars en la serie Clebsch-Gordan de , entonces debe aparecer en la serie Clebsch-Gordan de . Lo que implica,
Dónde
Como los coeficientes de Clebsch-Gordan son todos reales, se pueden deducir las siguientes propiedades de simetría,
Como los coeficientes de Clebsch-Gordan son todos reales, se pueden deducir las siguientes propiedades de simetría,
Dónde .
Grupo de simetría del operador hamiltoniano del oscilador 3D [ editar ]
Un hamiltoniano describe un oscilador armónico tridimensional.
donde la constante de resorte, la masa y la constante de Planck se han absorbido en la definición de las variables, ħ = m = 1 .
Se ve que este Hamiltoniano es simétrico bajo transformaciones de coordenadas que preservan el valor de . Por lo tanto, cualquier operador en el grupo SO (3) mantiene este invariante hamiltoniano.
Más importante aún, dado que el hamiltoniano es hermitiano, sigue siendo invariante bajo la operación de los elementos del grupo SU (3) mucho más grande .
Más sistemáticamente, operadores como los operadores de Escalera.
- y
se puede construir para que aumente y disminuya el valor propio del operador hamiltoniano en 1.
Los operadores â i y â i † no son hermitianos; pero los operadores hermitianos pueden construirse a partir de diferentes combinaciones de ellos,
- a saber, .
Hay nueve operadores de este tipo para i, j = 1,2,3.
Los nueve hermitianos formados por las formas bilineales â i † â j son controladas por los conmutadores fundamentales
Y visto para no conmutar entre sí. Como resultado, este conjunto completo de operadores no comparte sus vectores propios en común, y no pueden ser diagonalizados simultáneamente. Por lo tanto, el grupo no es abeliano y las degeneraciones pueden estar presentes en el hamiltoniano, como se indica.
El hamiltoniano del oscilador armónico isotrópico 3D, cuando está escrito en términos del operador asciende a
- .
El hamiltoniano tiene una degeneración de 8 veces. Una aplicación sucesiva de â i y â j † a la izquierda conserva el invariante Hamiltoniano, ya que aumenta N i en 1 y disminuye N j en 1, manteniendo así el total
- constante. (cf. oscilador armónico cuántico )
El conjunto máximo de operadores de conmutación [ editar ]
Dado que los operadores que pertenecen al grupo de simetría del Hamiltoniano no siempre forman un grupo abeliano , no se puede encontrar una base propia que diagonalice todos ellos simultáneamente. En su lugar, tomamos el máximo conjunto de operadores del grupo de simetría del Hamiltoniano, y tratamos de reducir las representaciones matriciales del grupo en representaciones irreductibles.
Espacio de Hilbert de dos sistemas [ editar ]
El espacio de Hilbert de dos partículas es el producto tensorial de los dos espacios de Hilbert de las dos partículas individuales,
dónde y Son el espacio de Hilbert de la primera y segunda partículas, respectivamente.
Los operadores en cada uno de los espacios de Hilbert tienen sus propias relaciones de conmutación, y un operador de un espacio de Hilbert conmuta con un operador del otro espacio de Hilbert. Así, el grupo de simetría del operador hamiltoniano de dos partículas es el superconjunto de los grupos de simetría de los operadores hamiltonianos de partículas individuales. Si los espacios individuales de Hilbert son N dimensionales, el espacio combinado de Hilbert es N 2 dimensional.
Coeficiente de Clebsch-Gordan en este caso [ editar ]
El grupo de simetría del hamiltoniano es SU (3) . Como resultado, los coeficientes de Clebsch-Gordan se pueden encontrar al expandir los vectores de base no acoplados del grupo de simetría del Hamiltoniano a su base acoplada. La serie Clebsch-Gordan se obtiene mediante la diagonalización en bloque del Hamiltoniano a través de la transformación unitaria construida a partir de los estados propios que diagonalizan el conjunto máximo de operadores que se desplazan diariamente.
Cuadros jóvenes [ editar ]
Un cuadro joven ( tableaux plural ) es un método para descomponer los productos de una representación de grupo SU ( N ) en una suma de representaciones irreductibles. Proporciona los tipos de dimensión y simetría de las representaciones irreductibles, que se conocen como la serie Clebsch-Gordan. Cada representación irreducible corresponde a un estado de partícula única y un producto de más de una representación irreducible indica un estado multipartícula.
Dado que las partículas son en su mayoría indistinguibles en la mecánica cuántica, esto se relaciona aproximadamente con varias partículas permutables. Las permutaciones de n partículas idénticas constituyen el grupo simétrico S n . Cada n estado partícula a de S n que se compone de los estados de una sola partícula de la fundamental N multiplete -dimensional SU (N) pertenece a una representación irreducible SU (N). Por lo tanto, se puede utilizar para determinar la serie Clebsch-Gordan para cualquier grupo unitario. [18]
Construyendo los estados [ editar ]
Cualquier función de onda de dos partículas., donde los índices 1, 2 representan el estado de las partículas 1 y 2, se pueden usar para generar estados de simetría explícita utilizando los operadores de simetría y anti-simetrización. [19]
donde el Son el operador que intercambia las partículas (operador de intercambio).
así,
Partiendo de un estado multipartícula, podemos aplicar y repetidamente para construir estados que son: [19] -
- Simétrico con respecto a todas las partículas.
- Antisimétrico con respecto a todas las partículas.
- Simetrías mixtas, es decir, simétricas o antisimétricas con respecto a algunas partículas.
La construcción de los tableaux [ editar ]
En lugar de usar ψ , en cuadros jóvenes, usamos cajas cuadradas ( □ ) para denotar partículas e i para denotar el estado de las partículas.
El conjunto completo de las partículas son denotadas por arreglos de □ s, cada uno con su propia etiqueta de número cuántico ( i ).
Los cuadros se forman apilando cajas lado a lado y de arriba a abajo, de manera que los estados simetrizados con respecto a todas las partículas se dan en una fila y los estados antimetrimétricos con respecto a todas las partículas se encuentran en una sola columna. Se siguen las siguientes reglas al construir los cuadros: [18]
- Una fila no debe ser más larga que la anterior.
- Las etiquetas cuánticas (números en el □ ) no deben disminuir mientras se va de izquierda a derecha en una fila.
- Las etiquetas cuánticas deben aumentar estrictamente mientras descienden en una columna.
Caso para N = 3 [ editar ]
Para N = 3 que es en el caso de SU (3), surge la siguiente situación. En SU (3) hay tres etiquetas, generalmente están designadas por (u, d, s) correspondientes a los quarks up, down y extraños que siguen el álgebra SU (3). También pueden ser designados genéricamente como (1,2,3). Para el sistema de dos partículas, tenemos los siguientes seis estados de simetría:
y los siguientes tres estados antisimétricos:
El cuadro de 1 columna y 3 filas es el singlete, por lo que todos los cuadros de irreps no triviales de SU (3) no pueden tener más de dos filas. La representación D (p, q) tiene p + q cuadros en la fila superior y q cuadros en la segunda fila.
Serie de Clebsch-Gordan de los cuadros [ editar ]
La serie Clebsch-Gordan es la expansión del producto directo de dos representaciones irreductibles a la suma directa de representaciones irreductibles. . Esto se puede encontrar fácilmente en los cuadros jóvenes.
Muestre elProcedimiento para obtener la serie Clebsch-Gordan de Tableaux joven:
Ejemplo de la serie Clebsch – Gordan para SU (3) [ editar ]
El producto tensorial de un triplete con un octeto que reduce a un deciquintuplet ( 15 ), un anti-sexteto y un triplete.
































![[\ hat {T}, \ hat {H}] = 0 = [\ hat {H}, \ hat {T}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ed50509a0924c5462d88ff27d95e5242433f1ed)








![{\ displaystyle [\ lambda _ {j}, \ lambda _ {k}] = 2if_ {jkl} \ lambda _ {l} ~,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3c33b47c48ad59ff19be70c039600caf798423c)


![{\ displaystyle f_ {ljk} = {\ frac {-i} {2}} \ mathrm {tr} ([\ lambda _ {l}, \ lambda _ {j}] \ lambda _ {k})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9554de14817068f164c685f6c3f915ba13fed1)









![[\ hat {Y}, \ hat {I} _3] = 0,](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdd1631937623957ed9fc47c5104d8444a0dac36)
![[\ hat {Y}, \ hat {I} _ \ pm] = 0,](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc8441e0b2009f422db1707d169b0379744d1c2a)
![[\ hat {Y}, \ hat {U} _ \ pm] = \ pm \ hat {U_ \ pm},](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd9b1922462153d7248cb9a4ed309563f545e97c)
![[\ hat {Y}, \ hat {V} _ \ pm] = \ pm \ hat {V_ \ pm},](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e425f0cdbd7bebf500ab941c4a429fd5efda604)
![[\ hat {I} _3, \ hat {I} _ \ pm] = \ pm \ hat {I_ \ pm},](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ddd2df89c50a53277ba800b6be55d432e725f69)
![[\ hat {I} _3, \ hat {U} _ \ pm] = \ mp \ frac {1} {2} \ hat {U_ \ pm},](https://wikimedia.org/api/rest_v1/media/math/render/svg/1933c20aee7b3712f222e073925003257b668bed)
![[\ hat {I} _3, \ hat {V} _ \ pm] = \ pm \ frac {1} {2} \ hat {V_ \ pm},](https://wikimedia.org/api/rest_v1/media/math/render/svg/83f711ab24d6095666c40475243c07dcaa8ff8e7)
![[\ hat {I} _ +, \ hat {I} _-] = 2 \ hat I_3,](https://wikimedia.org/api/rest_v1/media/math/render/svg/8621d656169896a18b3e05cf2ad09489737ce3d7)
![[\ hat {U} _ +, \ hat {U} _-] = \ frac {3} {2} \ hat {Y} - \ hat {I} _3,](https://wikimedia.org/api/rest_v1/media/math/render/svg/52ac8c9a2819cf2ba77dfab34271d5d4bbc0e813)
![[\ hat {V} _ +, \ hat {V} _-] = \ frac {3} {2} \ hat {Y} + \ hat {I} _3,](https://wikimedia.org/api/rest_v1/media/math/render/svg/99a4be38c3b81618cc9210f3abae808ded1d8a09)
![[\ hat {I} _ +, \ hat {V} _-] = - \ hat U_-,](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c5856073e2b679efdf550efc477545aeb81cebd)
![[{\ hat {I}} _ {+}, {\ hat {U}} _ {+}] = {\ hat V} _ {+},](https://wikimedia.org/api/rest_v1/media/math/render/svg/33b742132eebf245d82a3c4953f7757c16e74427)
![[\ hat {U} _ +, \ hat {V} _-] = \ hat I_-,](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9787268d8a7652d206eceb57d8e25dedc29748)
![[\ hat {I} _ +, \ hat {V} _ +] = 0,](https://wikimedia.org/api/rest_v1/media/math/render/svg/b625ba410c02609cb58fa91fb17e41c5efa27d62)
![[\ hat {I} _ +, \ hat {U} _-] = 0,](https://wikimedia.org/api/rest_v1/media/math/render/svg/4697cd30934ac45e0d74f274ae61a22ae263de07)
![[\ hat {U} _ +, \ hat {V} _ +] = 0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/313e596f5a2fe6a48f2327aaa77bed98e027fc55)













![[\ hat {I} _3, \ hat {Y}] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/863be8798da8a91f72f6cad113008e869a033c4c)









![{\ hat {U}} _ {0} \ equiv {\ frac {1} {2}} [{\ hat {U}} _ {+}, {\ hat {U}} _ {-}] = { \ frac {3} {4}} {\ hat {Y}} - {\ frac {1} {2}} {\ hat {I}} _ {3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8008bd20bd9bd5385a1ca341caee2b47f09b781)
![{\ hat {V}} _ {0} \ equiv {\ frac {1} {2}} [{\ hat {V}} _ {+}, {\ hat {V}} _ {-}] = { \ frac {3} {4}} {\ hat {Y}} + {\ frac {1} {2}} {\ hat {I}} _ {3}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e73135db79c56a44e970ebb9d39123f0ac334e0)



















































![{\ displaystyle [{\ hat {a_ {i}}}, {\ hat {a_ {j}}} ^ {\ dagger}] = \ delta _ {ij},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc31f2dbbbccabc20fb5b43baf90cd51850db898)
![[{\ hat {a_ {i}}}, {\ hat {a_ {j}}}] = [{\ hat {a_ {i}}} ^ {\ dagger}, {\ hat {a_ {j}} } ^ {\ daga}] = 0,](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d7805ffd2023a46695de5308b14e2d4e3594172)

![\ hat {H} = \ omega \ left [\ frac {3} {2} + \ hat {N_1} + \ hat {N_2} + \ hat {N_3} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bc6ec1850f1293e169561e57d54cc1a2be8a3b5)



























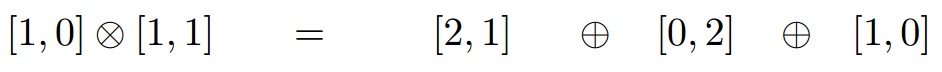
No hay comentarios:
Publicar un comentario