En termodinámica , el binodal , también conocido como curva de coexistencia o curva binodal , denota la condición en la que pueden coexistir dos fases distintas . De manera equivalente, es el límite entre el conjunto de condiciones en las que es termodinámicamente favorable para que el sistema se mezcle completamente y el conjunto de condiciones en las que es termodinámicamente favorable para que se separe de la fase. [1] En general, el binodal se define por la condición en la cual el potencial químico de todos los componentes de la solución es igual en cada fase. El extremo de una curva binodal en temperatura coincide con el del spinodal.Curva y es conocido como un punto crítico .
Sistemas binarios [ editar ]
En mezclas binarias (de dos componentes), el binodal se puede determinar a una temperatura dada dibujando una línea tangente a la energía libre.
La termodinámica biológica es el estudio cuantitativo de las transducciones de energía que ocurren en o entre los organismos vivos, estructuras y células, y de la naturaleza y función de los procesos químicos subyacentes a estas transducciones. La termodinámica biológica puede abordar la cuestión de si el beneficio asociado con algún rasgo fenotípico particular vale la inversión de energía que requiere.
Historia [ editar ]
El médico médico y bioquímico alemán-británico Hans Krebs ' Transformaciones de energía en la materia viva de1957 (escrito con Hans Kornberg ) [1] fue la primera publicación importante sobre la termodinámica de las reacciones bioquímicas. Además, el apéndice contenía las primeras tablas termodinámicas publicadas, escritas por Kenneth Burton , para contener constantes de equilibrio y energía libre de Gibbs de formaciones para especies químicas , capaces de calcular reacciones bioquímicas que aún no habían ocurrido.
Se ha aplicado la termodinámica de no equilibrio para explicar cómo los organismos biológicos pueden desarrollarse a partir del desorden. Ilya Prigogine desarrolló métodos para el tratamiento termodinámico de tales sistemas. Llamó a estos sistemas sistemas disipativos , porque son formados y mantenidos por los procesos disipativos que intercambian energía entre el sistema y su entorno, y porque desaparecen si ese intercambio cesa. Se puede decir que viven en simbiosis con su entorno. Las transformaciones de energía en biología dependen principalmente de la fotosíntesis . La energía total captada por la fotosíntesis en las plantas verdes de la radiación solar es de aproximadamente 2 x 10 23 julios de energía por año. [2]La energía anual capturada por la fotosíntesis en las plantas verdes es aproximadamente el 4% de la energía total de la luz solar que llega a la Tierra. Las transformaciones de energía en las comunidades biológicas que rodean los respiraderos hidrotermales son excepciones; oxidan el azufre , obteniendo su energía a través de la quimiosíntesis en lugar de la fotosíntesis.
El enfoque de la termodinámica en biología [ editar ]
El campo de la termodinámica biológica se centra en los principios de la termodinámica química en biología y bioquímica . Los principios cubiertos incluyen la primera ley de la termodinámica , la segunda ley de la termodinámica , la energía libre de Gibbs , la termodinámica estadística , la cinética de reacción y las hipótesis del origen de la vida. Actualmente, la termodinámica biológica se ocupa del estudio de la dinámica bioquímica interna como: hidrólisis de ATP, estabilidad de proteínas, unión de ADN, difusión de membrana, cinética de enzimas, [3]y otras vías de control de energía esencial. En términos de la termodinámica, la cantidad de energía capaz de hacer un trabajo durante una reacción química se mide cuantitativamente por el cambio en la energía libre de Gibbs . El biólogo físico Alfred Lotka intentó unificar el cambio en la energía libre de Gibbs con la teoría evolutiva.
Transformación de la energía en los sistemas biológicos [ editar ]
El sol es la principal fuente de energía para los organismos vivos. Algunos organismos vivos como las plantas necesitan la luz solar directamente, mientras que otros organismos como los humanos pueden adquirir energía del sol indirectamente. [4] Sin embargo, hay evidencia de que algunas bacterias pueden prosperar en ambientes hostiles como la Antártida como evidencia de las algas verde-azules debajo de capas gruesas de hielo en los lagos. Independientemente del tipo de especie viva, todos los organismos vivos deben capturar, transducir, almacenar y utilizar la energía para vivir.
La relación entre la energía de la luz solar entrante y su longitud de onda λ o frecuencia ν viene dada por
donde h es la constante de Planck (6.63x10 −34 Js) y c es la velocidad de la luz (2.998x10 8 m / s). Las plantas atrapan esta energía de la luz solar y se someten a la fotosíntesis, convirtiendo efectivamente la energía solar en energía química. Para transferir la energía una vez más, los animales se alimentarán de las plantas y utilizarán la energía de los materiales vegetales digeridos para crear macromoléculas biológicas.
Teoría termodinámica de la evolución [ editar ]
La evolución biológica puede explicarse a través de una teoría termodinámica. Las cuatro leyes de la termodinámica se utilizan para enmarcar la teoría biológica detrás de la evolución . La primera ley de la termodinámica establece que los estados no pueden crearse o destruirse. Ninguna vida puede crear energía, sino que debe obtenerla a través de su entorno. La segunda ley de la termodinámica establece que la energía se puede transformar y que ocurre todos los días en las formas de vida. A medida que los organismos toman energía de su entorno, pueden transformarla en energía útil. Esta es la base de la dinámica tropical.
El ejemplo general es que el sistema abierto se puede definir como cualquier ecosistema que se mueve hacia la maximización de la dispersión de energía. Todas las cosas se esfuerzan por lograr la máxima producción de entropía , lo que en términos de evolución ocurre en cambios en el ADN para aumentar la biodiversidad . Así, la diversidad puede estar vinculada a la segunda ley de la termodinámica. También se puede argumentar que la diversidad es un proceso de difusión que se difunde hacia un equilibrio dinámico para maximizar la entropía. Por lo tanto, la termodinámica puede explicar la dirección y la velocidad de evolución junto con la dirección y la velocidad de sucesión. [5]
Ejemplos [ editar ]
Primera Ley de la Termodinámica [ editar ]
La Primera Ley de la Termodinámica es una declaración de la conservación de la energía; aunque se puede cambiar de una forma a otra, la energía no se puede crear ni destruir. [6] De la primera ley, surge un principio llamado Ley de Hess . La Ley de Hess establece que el calor absorbido o evolucionado en una reacción dada siempre debe ser constante e independiente de la manera en que se produce la reacción. Aunque algunas reacciones intermedias pueden ser endotérmicas y otras pueden ser exotérmicas, el intercambio de calor total es igual al intercambio de calor si el proceso se hubiera producido directamente. Este principio es la base del calorímetro., un dispositivo utilizado para determinar la cantidad de calor en una reacción química. Como toda la energía entrante ingresa al cuerpo como alimento y finalmente se oxida, la producción total de calor se puede estimar midiendo el calor producido por la oxidación de los alimentos en un calorímetro. Este calor se expresa en kilocalorías , que son la unidad común de energía alimentaria que se encuentra en las etiquetas nutricionales. [7]
Segunda Ley de la Termodinámica [ editar ]
La Segunda Ley de la Termodinámica se ocupa principalmente de si un proceso dado es posible o no. La Segunda Ley establece que no puede ocurrir ningún proceso natural a menos que esté acompañado por un aumento en la entropía del universo. [8] Dicho de otra manera, un sistema aislado siempre tenderá al desorden. A menudo se cree erróneamente que los organismos vivos desafían la Segunda Ley porque pueden aumentar su nivel de organización. Para corregir esta mala interpretación, uno debe referirse simplemente a la definición de sistemas y límites. Un organismo vivo es un sistema abierto, capaz de intercambiar materia y energía con su entorno. Por ejemplo, un ser humano ingiere alimentos, los descompone en sus componentes y luego los utiliza para formar células, tejidos, ligamentos, etc. Este proceso aumenta el orden en el cuerpo y, por lo tanto, disminuye la entropía. Sin embargo, los humanos también 1) conducen el calor a la ropa y otros objetos con los que están en contacto, 2) generan convección debido a las diferencias en la temperatura corporal y el ambiente, 3) irradian calor al espacio, 4) consumen sustancias que contienen energía (es decir, alimentos), y 5) eliminar los desechos (por ejemplo, dióxido de carbono, agua y otros componentes de la respiración, orina, heces, sudor, etc.). Al tomar en cuenta todos estos procesos, aumenta la entropía total del sistema mayor (es decir, el entorno humano y su entorno). Cuando el humano deja de vivir,
Gibbs Free Energy [ editar ]
En los sistemas biológicos, en general la energía y la entropía cambian juntas. Por lo tanto, es necesario poder definir una función de estado que explique estos cambios simultáneamente. Esta función de estado es la energía libre de Gibbs, G .
- G = H - TS
dónde:
- H es la entalpía (unidad SI: julios)
- T es la temperatura (unidad SI: kelvin )
- S es la entropía (unidad SI: julios por kelvin)
El cambio en la Energía Libre de Gibbs se puede usar para determinar si una reacción química dada puede ocurrir espontáneamente. Si ∆ G es negativo, la reacción puede ocurrir espontáneamente . Del mismo modo, si ∆ G es positivo, la reacción es no espontánea. [9] Las reacciones químicas se pueden "juntar" juntas si comparten intermedios. En este caso, el cambio total de Energía Libre de Gibbs es simplemente la suma de los valores de ∆ G para cada reacción. Por lo tanto, una reacción desfavorable (positiva ∆ G 1 ) puede ser impulsada por una segunda reacción altamente favorable (negativa ∆ G 2 donde la magnitud de ∆ G 2 > magnitud de ∆ G1 ). Por ejemplo, la reacción de la glucosa con fructosa para formar sacarosa tiene un valor de G de +5.5 kcal / mol. Por lo tanto, esta reacción no ocurrirá espontáneamente. La descomposición del ATP para formar ADP y fosfato inorgánico tiene un valor de ∆ G de -7.3 kcal / mol. Estas dos reacciones se pueden acoplar juntas, de modo que la glucosa se une con el ATP para formar glucosa-1-fosfato y ADP. La glucosa-1-fosfato es capaz de unirse a la fructosa produciendo sacarosa y fosfato inorgánico. El valor de ∆ G de la reacción acoplada es -1.8 kcal / mol, lo que indica que la reacción se producirá espontáneamente. Este principio de acoplamiento de reacciones para alterar el cambio en Gibbs Free Energy es el principio básico detrás de toda acción enzimática en organismos biológicos.
Una gráfica de Bjerrum (llamada así por Niels Bjerrum ) es una gráficade las concentraciones de las diferentes especies de un ácido polipróticoen una solución , como funciones del pH de la solución , [1] cuando la solución está en equilibrio . Debido a los muchos órdenes de magnitudabarcados por las concentraciones, generalmente se trazan en una escala logarítmica . A veces, las proporciones de las concentraciones se representan más que las concentraciones reales. Ocasionalmente ,también se grafican H + y OH .
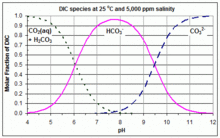
La mayoría de las veces, el sistema de carbonato se traza, donde el ácido poliprótico es ácido carbónico (un ácido diprótico ), y las diferentes especies son ácido carbónico , dióxido de carbono , bicarbonato y carbonato . En condiciones ácidas, la forma dominante es el CO 2 ; en condiciones básicas (alcalinas), la forma dominante es CO 3 2− ; y en el medio, la forma dominante es HCO 3 - . En cada pH, se supone que la concentración de ácido carbónico es despreciable en comparación con la concentración de CO2 ., y así se omite a menudo en las parcelas de Bjerrum. Estas parcelas se utilizan normalmente en la química oceánica para rastrear la respuesta de un océano a los cambios en el pH y en los insumos en carbonato y CO
2 . [2]
2 . [2]
Las parcelas de Bjerrum para otros ácidos polipróticos, incluidos los ácidos silícico , bórico , sulfúrico y fosfórico , también se pueden construir.
Ecuaciones de la gráfica de Bjerrum para el sistema de carbonato [ editar ]
Si el dióxido de carbono , el ácido carbónico , los iones de hidrógeno , el bicarbonato y el carbonato se disuelven en agua , y en el equilibrio químico , a menudo se supone que sus concentraciones de equilibrio vienen dadas por:
donde el subíndice 'eq' indica que estas son concentraciones de equilibrio, K 1 es la constante de equilibrio para la reacción CO
2 +H
2 O⇌ H++ HCO3-(es decir, la primeraconstante de disociación ácidapara el ácido carbónico),K2 es laconstante de equilibriopara la reacción HCO3-⇌ H++ CO32−(es decir, la segundaconstante de disociación ácidapara el carbono ácido), y DIC es laconcentracióntotal (invariable)decarbono inorgánico disueltoen el sistema, es decir, [CO2] + [HCO3-] + [CO32−]. K 1 ,K 2 y DIC tienen unidades de una concentración , por ejemplo, mol / litro .
2 +H
2 O⇌ H++ HCO3-(es decir, la primeraconstante de disociación ácidapara el ácido carbónico),K2 es laconstante de equilibriopara la reacción HCO3-⇌ H++ CO32−(es decir, la segundaconstante de disociación ácidapara el carbono ácido), y DIC es laconcentracióntotal (invariable)decarbono inorgánico disueltoen el sistema, es decir, [CO2] + [HCO3-] + [CO32−]. K 1 ,K 2 y DIC tienen unidades de una concentración , por ejemplo, mol / litro .
Se obtiene un gráfico de Bjerrum utilizando estas tres ecuaciones para representar estas tres especies contra pH = - log 10 [H + ] eq , para K 1 , K 2 y DIC dados . Las fracciones en estas ecuaciones dan las proporciones relativas de las tres especies y, por lo tanto, si se desconoce la DIC o si las concentraciones reales no son importantes, estas proporciones pueden representarse en su lugar.
Estas tres ecuaciones muestran que las curvas para CO 2 y HCO 3 - se intersecan en [H + ] eq = K 1 , y las curvas para HCO 3 - y CO 3 2 - se intersecan en [H + ] eq = K 2 . Por lo tanto, los valores de K 1 y K 2 que se usaron para crear una gráfica Bjerrum dada se pueden encontrar fácilmente en esa gráfica, leyendo las concentraciones en estos puntos de intersección. En el gráfico adjunto se muestra un ejemplo con eje Y lineal. Cabe señalar que los valores de K1 y K 2 , y por lo tanto las curvas en el gráfico de Bjerrum, varían sustancialmente con la temperatura y la salinidad. [3]
Derivación química y matemática de las ecuaciones de la gráfica de Bjerrum para el sistema de carbonato [ editar ]
Supongamos que las reacciones entre dióxido de carbono , iones de hidrógeno , bicarbonato e iones de carbonato , todas disueltas en agua , son las siguientes:
- CO
2 +H
2 O⇌ H++ HCO3- (1) - HCO 3 - ⇌ H + + CO 3 2− . (2)
(Tenga en cuenta que la reacción (1) es en realidad la combinación de dos reacciones elementales : CO
2+H
2 O⇌H
2 CO
3 ⇌ H++ HCO3-.)
2+H
2 O⇌H
2 CO
3 ⇌ H++ HCO3-.)
Suponiendo que la ley de acción de masas se aplique a estas dos reacciones, que el agua es abundante y que las diferentes especies químicas están siempre bien mezcladas, sus ecuaciones de velocidad son
donde [ ] denota concentración , t es tiempo, y k 1 y k −1 son constantes de proporcionalidad apropiadas para la reacción (1), llamadas respectivamente las constantes de velocidad hacia adelante y hacia atrás para esta reacción. (Similarmente k 2 y k −2 para la reacción (2).)
En cualquier equilibrio , las concentraciones no cambian, por lo tanto, los lados izquierdos de estas ecuaciones son cero. Entonces, a partir de la primera de estas cuatro ecuaciones, la relación de las constantes de velocidad de la reacción (1) es igual a la relación de sus concentraciones de equilibrio, y esta relación, llamada K 1 , se llama la constante de equilibrio para la reacción (1), es decir
- (3)
donde el subíndice 'eq' denota que estas son concentraciones de equilibrio.
- (4)
Reorganizar (3) da
- (5)
y reorganizando (4), luego sustituyendo en (5), da
- (6)
- sustituyendo en (5) y (6)
Reorganizar esto da la ecuación para CO
2 :
2 :
Las ecuaciones para HCO 3 - y CO 3 2− se obtienen sustituyendo esto en (5) y (6).
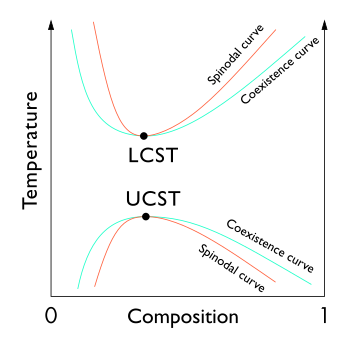


![[{\ textrm {CO}} _ {2}] _ {{eq}} = {\ frac {[{\ textrm {H}} ^ {+}] _ {{eq}} ^ {2}} {[ {\ textrm {H}} ^ {+}] _ {{eq}} ^ {2} + K_ {1} [{\ textrm {H}} ^ {+}] _ {{eq}} + K_ {1 } K_ {2}}} \ times {\ textrm {DIC}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c64507f41a8e6cc124f36d34dc941c5ec97d447)
![[{\ textrm {HCO}} _ {3} ^ {-}] _ {{eq}} = {\ frac {K_ {1} [{\ textrm {H}} ^ {+}] _ {{eq} }} {[{\ textrm {H}} ^ {+}] _ {{eq}} ^ {2} + K_ {1} [{\ textrm {H}} ^ {+}] _ {{eq}} + K_ {1} K_ {2}}} \ times {\ textrm {DIC}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/c69c378ff186a1351ef7c3b8518be7c0ee3c6387)
![[{\ textrm {CO}} _ {3} ^ {{2 -}}] _ {{eq}} = {\ frac {K_ {1} K_ {2}} {[{\ textrm {H}} ^ {+}] _ {{eq}} ^ {2} + K_ {1} [{\ textrm {H}} ^ {+}] _ {{eq}} + K_ {1} K_ {2}}} \ veces {\ textrm {DIC}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/77e886a8ee430a6964c2ad580a8675b151eb9dfb)
![{\ frac {{\ textrm {d}} [{\ textrm {CO}} _ {2}]} {{\ textrm {d}} t}} = - k_ {1} [{\ textrm {CO}} _ {2}] + k _ {{- 1}} [{\ textrm {H}} ^ {+}] [{\ textrm {HCO}} _ {3} ^ {-}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/6de134b2361770f97043336485841e9b71760ab0)
![{\ frac {{\ textrm {d}} [{\ textrm {H}} ^ {+}]} {{\ textrm {d}} t}} = k_ {1} [{\ textrm {CO}} _ {2}] - k _ {{- 1}} [{\ textrm {H}} ^ {+}] [{\ textrm {HCO}} _ {3} ^ {-}] + k_ {2} [{\ textrm {HCO}} _ {3} ^ {-}] - k _ {{- 2}} [{\ textrm {H}} ^ {+}] [{\ textrm {CO}} _ {3} ^ {{ 2-}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/e14806de144e5fcf23f83fa45c0076f01aa8438e)
![{\ frac {{\ textrm {d}} [{\ textrm {HCO}} _ {3} ^ {-}]} {{\ textrm {d}} t}} = k_ {1} [{\ textrm { CO}} _ {2}] - k _ {{- 1}} [{\ textrm {H}} ^ {+}] [{\ textrm {HCO}} _ {3} ^ {-}] - k_ {2 } [{\ textrm {HCO}} _ {3} ^ {-}] + k _ {{- 2}} [{\ textrm {H}} ^ {+}] [{\ textrm {CO}} _ {3 } ^ {{2-}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/075781675b0f5e1a8e01f32cd7ce7298583aebcf)
![{\ frac {{\ textrm {d}} [{\ textrm {CO}} _ {3} ^ {{2 -}}]} {{\ textrm {d}} t}} = k_ {2} [{ \ textrm {HCO}} _ {3} ^ {-}] - k _ {{- 2}} [{\ textrm {H}} ^ {+}] [{\ textrm {CO}} _ {3} ^ { {2-}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/88d34d5cd11198310bc9611e942e58228a519b8c)
![K_ {1} = {\ frac {k_ {1}} {k _ {{- 1}}}} = {\ frac {[{\ textrm {H}} ^ {+}] _ {{eq}} [{ \ textrm {HCO}} _ {3} ^ {-}] _ {{eq}}} {[{\ textrm {CO}} _ {2}] _ {{eq}}}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/34a8bbf9e461643a80970e7c88bf90b606e1d20a)
![K_ {2} = {\ frac {k_ {2}} {k _ {{- 2}}}} = {\ frac {[{\ textrm {H}} ^ {+}] _ {{eq}} [{ \ textrm {CO}} _ {3} ^ {{2 -}}] _ {{eq}}} {[{\ textrm {HCO}} _ {3} ^ {-}] _ {{eq}}} }.](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbd12f7f452c8bc79923b48813a7d4fbbd08cc79)
![[{\ textrm {HCO}} _ {3} ^ {-}] _ {{eq}} = {\ frac {K_ {1} [{\ textrm {CO}} _ {2}] _ {{eq} }} {[{\ textrm {H}} ^ {+}] _ {{eq}}}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c44829914c17f8790c48e2479f8446795da6f55)
![{\ displaystyle [{\ textrm {CO}} _ {3} ^ {2 -}] _ {eq} = {\ frac {K_ {2} [{\ textrm {HCO}} _ {3} ^ {-} ] _ {eq}} {[{\ textrm {H}} ^ {+}] {{eq}}} = {\ frac {K_ {1} K_ {2} [{\ textrm {CO}} _ {2 }] _ {eq}} {[{\ textrm {H}} ^ {+}] _ {eq} ^ {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d79fa6859b32f926456d0aee3e455151b648768d)
![{\ textrm {DIC}} = [{\ textrm {CO}} _ {2}] + [{\ textrm {HCO}} _ {3} ^ {-}] + [{\ textrm {CO}} _ { 3} ^ {{2-}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1bbbc5a0e1e41f64eef87842b2a93da7ff5b6de)
![= [{\ textrm {CO}} _ {2}] _ {{eq}} \ left (1 + {\ frac {K_ {1}} {[{\ textrm {H}} ^ {+}] _ { {eq}}}} + {\ frac {K_ {1} K_ {2}} {[{\ textrm {H}} ^ {+}] _ {{eq}} ^ {2}}} \ right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b284790aacdd68f00a7ff8e4ee2dab0c0a1eb1d)
![{\ displaystyle = [{\ textrm {CO}} _ {2}] _ {eq} \ left ({\ frac {[{\ textrm {H}} ^ {+}] _ {eq} ^ {2} + K_ {1} [{\ textrm {H}} ^ {+}] _ {eq} + K_ {1} K_ {2}} {[{\ textrm {H}} ^ {+}] _ {eq} ^ {2}}} \ derecha).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a63cc82397b76126c5364516eb688702a6ed6e54)
![[{\ textrm {CO}} _ {2}] _ {{eq}} = {\ frac {[{\ textrm {H}} ^ {+}] _ {{eq}} ^ {2}} {[ {\ textrm {H}} ^ {+}] _ {{eq}} ^ {2} + K_ {1} [{\ textrm {H}} ^ {+}] _ {{eq}} + K_ {1 } K_ {2}}} \ times {\ textrm {DIC}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e27f7abfe747c293e20cd24fc680b1f76087f28)
No hay comentarios:
Publicar un comentario