Ciclo
Es cada porción de un movimiento periódico que, repetido cíclicamente, da lugar al movimiento periódico completo.
Así por ejemplo, en el mecanismo de yugo escocés representado en la figura, cuando el eslabón 2 gira con velocidad angular w constante, dicho eslabón 2 realiza un movimiento periódico, en donde cada vuelta completa del eslabón es un ciclo.

Así por ejemplo, en el mecanismo de yugo escocés representado en la figura, cuando el eslabón 2 gira con velocidad angular w constante, dicho eslabón 2 realiza un movimiento periódico, en donde cada vuelta completa del eslabón es un ciclo.
Circulo de Mohr de tensiones
El círculo de Mohr de tensiones es una aplicación del círculo de Mohr al cálculo de las tensiones en planos con distintas orientaciones alrededor de un punto de una pieza sometido a un estado tensional biaxial.
Si se dibuja un elemento diferencial alrededor del punto analizado, con dos planos orientados según un sistema de ejes plano x-y y el tercero inclinado un ángulo genérico φ estableciendo el equilibrio de fuerzas en las direcciones de σ y τ en dicho elemento se tiene:
Dividiendo las dos ecuaciones anteriores por la longitud AB y teniendo en cuenta que OA=AB·cos(φ), OB=AB·sen(φ) se llega a:
expresión que también puede escribirse como:
Derivando la primera ecuación (3) respecto a φ e igualando a cero se obtienen los valores de φ (inclinaciones del plano AB) para los que la tensión normal es máxima o mínima:
Ecuación que tiene dos soluciones de φ. Sustituyendo cada una de las soluciones en la segunda de las ecuaciones (3) se comprueba que la tensión cortante es nula para dichos planos y sustituyendo en la primera de las ecuaciones (3) se obtienen las tensiones normales máxima y mínima (tensiones principales):
La expresión de las tensiones en cualquier plano con inclinación φ respecto a los planos principales, en función de las tensiones principales, se deduce tomando las direcciones x,y orientadas según los planos principales y sustituyendo en (3):
El círculo de Mohr de tensiones es un círculo dibujado en el plano σ-τ en el que cada punto de su circunferencia representa las tensiones normales y cortantes en un plano AB con una inclinación cualquiera. Así los puntos X e Y de la figura corresponden a los planos perpendiculares a los ejes x e y. Como se observa se sitúan en puntos opuestos del círculo, a 180º. Los puntos de corte de la circunferencia con el eje τ =0 corresponden a los planos principales y de la figura se deduce que el valor de σ en dichos puntos es el valor de las tensiones principales (σ1,σ2) obtenido mediante las ecuaciones (5). Estos planos están igualmente separados un ángulo de 180º en el círculo, indicando que el ángulo entre los planos principales es de 90º en la realidad. En general, dos planos entre los cuales hay un ángulo φ en la realidad están separados un ángulo 2φ en el círculo de Mohr. En la figura se observa también que el ángulo φ entre los planos principales y los planos x,y, obtenido mediante la expresión (4) queda representado por 2φen el círculo de Mohr. El círculo de Mohr se utiliza como recurso gráfico para el análisis de las tensiones en estados tensionales biaxiales. Para dibujar correctamente el círculo de Mohr deben tenerse en cuenta los siguientes detalles:
CIRCULO DE MOHR.
Las ecuaciones sig. Son las ecuaciones paramétricas de una circunferencia. Ox + Oy = Ox - O cos 2Ø - txy sen 2Ø On - 2 _ 2 t = OX - OY sen 2Ø + txy cos 2Ø Elevado al cuadrado, sumado y simplificado, ( On - Ox + Oy) 2 + t 2 = ( Ox – Oy ) 2 + ( txy ) 2 2 2 Recordemos que Ox , OY y txy son constantes conocidas que definen el estado plano de tensión, mientras que O y t son variables. Por tanto, Ox + Oy/2 es una constantes C, y el segundo miembro de la ecuación (c) es otra constante R2. con esta substituciones, la ecuación (c) se transforma en : ( On – C ) 2 + t2 = R2 de la forma ( x – C )2 + y2 = R2. representa, por tanto, una circunferencia de radio R= 2Del origen de abcisas. La sig. Figura representa la circunferencia de Mohr para el estado plano de tensiones que se ha estudiado en la seccion anterior. El centro C esta a una distancia OC del origen que es la media aritmética de las tensiones normales, y el radio R es la hipotenusa del triangulo rectángulo CDA. Se puede comprobar fácilmente que las coordenadas de los puntos E, F, G corresponden a las expresiones deducidas en las ecuaciones, y se vera como la circunferencia de Mohr representa gráficamente la variación de las tensiones dadas por las ecuaciones. Las reglas siguientes resumen la construcción de la circunferencia de Mohr. 1.- Sobre un sistema de ejes coordenadas rectangulares On – t , se sitúan los puntos de coordenadas ( Ox , txy ) y ( Oy , txy ). Estos puntos representan las tensiones normales y cortantes que actúan sobre las caras X e Y de un elemento. Se considera positiva la tracción y negativa la compresión; la tensión cortante es positiva si el momento del centro del elemento es de sentido horario. 2.- Se unen los puntos situados mediante una recta. El segmento de dicha recta comprendido entre los dos puntos es el diámetro de una circunferencia cuyo centro es la intersección con el eje O. 3.- Para los diferentes planos que pasan por el punto en estudio, las componentes de la tensión, normal y cortante, están representadas por las coordenadas de un punto que se mueve por la circunferencia de Mohr. 4.- El radio con sentido hacia un punto de la circunferencia representa al eje normal al plano cuyas componentes de la tensión viene dadas por las coordenadas del punto de la circunferencia. 5.- El ángulo entre los radios de dos puntos de la circunferencia de Mohr es el doble del ángulo entre las normales a los dos planos que representan estos dos puntos. El sentido de rotación del ángulo es el mismo en la circunferencia que en la realidad, es decir, si el eje N forma ángulo O con el eje X en sentido antihorario, el radio N del circulo forma un ángulo de 20 con el radio X en sentido antihorario. 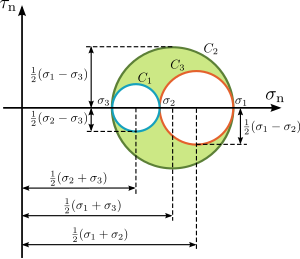 |
No hay comentarios:
Publicar un comentario