3-esfera
En geometría, 3-esfera es la superficie de una esfera, mientras que en topología se refieren a ella como una 2-esfera y la indican como  .1 Llamativamente, geómetras y topólogos adoptan convenios incompatibles para el significado de "n-esfera".
.1 Llamativamente, geómetras y topólogos adoptan convenios incompatibles para el significado de "n-esfera".
 .1 Llamativamente, geómetras y topólogos adoptan convenios incompatibles para el significado de "n-esfera".
.1 Llamativamente, geómetras y topólogos adoptan convenios incompatibles para el significado de "n-esfera".
Proyección estereográfica de los paralelos de una hiperesfera (rojo), los meridianos (azul) y los hipermeridianos (verde). Debido a la propiedadconforme de la proyección estereográfica, todas estas curvas se intersecan unas a otras ortogonalmente (en los puntos amarillos) como en 4D. Todas las curvas son círculos: las curvas que se intersecan en <0> tienen radio infinito (= líneas rectas).
3-esfera en topología
En topología, una 3-esfera o hiperesfera es análoga a una esfera en un espacio de mayor número de dimensiones. Una esfera ordinaria, o 2-esfera, consiste de todos los puntos equidistantes de un punto dado en elespacio euclídeo tridimensional ordinario, R3. Una 3-esfera consiste de todos los puntos equidistantes de un punto dado en R4. Mientras que una 2-esfera es una superficie "suave" de dos dimensiones, una 3-esfera es un ejemplo de una 3-variedad.
De forma enteramente análoga, es posible definir esferas de un número de dimensiones mayor, llamadas hiperesferas o n-esferas. Dichos objetos son variedades n-dimensionales.
Alguna literatura se refiere a la 3-esfera como glomo, del latín glomus, balón. Informalmente, un glomo es a una esfera lo que ésta es a un círculo.
Definición
En coordenadas, una 3-esfera con centro (x0, y0, z0, w0) y radio r es el conjunto de todos los puntos (x, y, z, w) en R4 tales que
La 3-esfera centrada en el origen y con radio 1 se llama 3-esfera unitaria o 3-esfera unidad, y habitualmente se denota S3. Puede ser descrita como un subconjunto deR4, de C2, o de H (los cuaterniones):
La última descripción es habitualmente la más útil. Describe la 3-esfera como el conjunto de todos los cuaterniones unidad, es decir, los cuaterniones con valor absoluto igual a 1. Así como el conjunto de todos los números complejos unidad es importante en geometría compleja, el conjunto de todos los cuaterniones unidad es importante para la geometría de los cuaterniones.
Propiedades
El volumen tridimensional (o hiperárea) de una 3-esfera de radio r es
mientras que el hipervolumen tetradimensional (el volumen de la región de 4 dimensiones delimitada por la 3-esfera) es
Cada intersección no vacía de una 3-esfera con un hiperplano tridimensional es una 2-esfera, a menos que el hiperplano sea tangente a la 3-esfera, en cuyo caso la intersección es un único punto. Cuando la 3-esfera se mueve a través de un hiperplano tridimensional dado, la intersección comienza como un punto, luego se convierte en una 2-esfera creciente que alcanza su tamaño máximo cuando el hiperplano corta directamente a través del "medio" de la 3-esfera, y finalmente la 2-esfera se "encoge" nuevamente hasta ser un solo punto a medida que la 3-esfera abandona el hiperplano.
Propiedades topológicas
Una 3-esfera es una variedad compacta sin delimitación. También es simplemente conexa. Lo que esto significa, informalmente, es que cualquier camino circular, o cualquier rizo, en la 3-esfera puede encogerse continuamente a un punto sin abandonar la 3-esfera. Existe desde hace tiempo una conjetura, llamada conjetura de Poincaré, que sostiene que la 3-esfera es la única variedad tridimensional con estas propiedades (salvo homeomorfismo). Aparentemente, esta conjetura ha sido probada por Grigori Perelmán en una serie de trabajos producidos a partir de noviembre de 2002.
La 3-esfera es también homeomórfica con la compactación en un punto R3.
Los grupos de homología no triviales de la 3-esfera son los siguientes: H0(S3,Z) y H3(S3,Z) son ambos cíclicos infinitos, mientras que Hi(S3,Z) = {0} para todo otro índice i. Cualquier espacio topológico con estos grupos de homología es conocido como una 3-esfera homológica. Inicialmente Poincaré conjeturó que todas las 3-esferas de homología eran homomórficas a S3, pero luego logró construir una no homomórfica, ahora conocida como la esfera de Poincaré. Se conoce la existencia de un número infinito de esferas de homología. Por ejemplo, un llenado de Dehn con pendiente 1/n sobre cualquier nudo en la 3-esfera da una esfera de homología; típicamente, éstas no son homomorfas de la 3-esfera.
Respecto de los grupos de homotopía, tenemos π1(S3) = π2(S3) = {0} y π3(S3) es cíclico infinito. Los grupos de homotopia más grandes (k ≥ 4) son todos abelianos finitos, pero además de ello no siguen ningún patrón discernible. Para mayor detalle, véase grupos de homotopia de las esferas.
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| πk(S3) | 0 | 0 | 0 | Z | Z2 | Z2 | Z12 | Z2 | Z2 | Z3 | Z15 | Z2 | Z2⊕Z2 | Z12⊕Z2 | Z84⊕Z2⊕Z2 | Z2⊕Z2 | Z6 |
Hay una interesante acción de grupo de S1 (imaginado como el grupo de los números complejos de valor absoluto 1) sobre S3 (imaginada como un subconjunto de C2): λ·(z1,z2) = (λz1,λz2). El espacio orbital de esta acción es naturalmente homomorfo con la 2-esfera S2. El mapa resultante de la 3-esfera en la 2-esfera es conocido comohaz de Hopf. Es el generador del grupo de homotopia π3(S2).
Estructura de grupo
Cuando se la considera como el conjunto de los cuaterniones unidad, S3 hereda la estructura de la multiplicación cuaterniónica. Dado que el conjunto de los cuaterniones unidad es cerrado bajo la multiplicación S3 tiene la estructura de un grupo. Además, como la multiplicación cuaterniónica es regular (infinitamente diferenciable), S3 puede ser visto como un grupo de Lie. Es un grupo de Lie que no es abeliano, compacto, de dimensión 3. Cuando se lo imagina como un grupo de Lie se lo suele denotar Sp(1) o U(1, H).
Resulta ser que las únicas esferas que admiten la estructura de un grupo de Lie son el círculo unidad, S1, imaginado como el cojunto de los números complejos unidad, y S3, el conjunto de los cuaterniones unidad. Se podría pensar que S7, el conjunto de los octoniones unidad, formaría un grupo de Lie, pero esto no es así porque la multiplicación de octoniones no es asociativa. La estructura octoniónica da a S7 una importante propiedad: la paralelizabilidad. Las únicas esferas paralelizables son S1,S3 y S7.
Usando una representación matricial de los cuaterniones, H, se obtiene una representación matricial de S3. Una elección conveniente es
Este mapa da un homomorfismo algebraico inyectivo de H en el conjunto de matrices complejas 2×2. Tiene la propiedad de que el valor absoluto de un cuaternión q es igual a la raíz cuadrada del determinante de la matriz imagen de q.
El conjunto de los cuaterniones unidad está por lo tanto dado por matrices de la forma arriba indicada con determinante unidad. Resulta que este grupo es precisamente el grupo especial unitario SU(2). Por lo tanto S3 como grupo de Lie es isomorfo a SU(2).
Usiando nuestras coordenadas hiperesféricas (η, ξ1, ξ2) podemos escribir cualquier elemento de SU(2) como
Sistemas de coordenadas sobre la 3-esfera
Coordenadas hiperesféricas
Resulta conveniente contar con algún tipo de coordenadas hiperesféricas en S3, análogamente a las coordenadas esféricas usuales en S2. Una elección (de ningún modo la única posible) es utilizar (ψ, θ, φ) donde
donde ψ y θ se desplazan en el rango de (0,π), y φ se desplaza en (0,2π), donde al igual que en el caso de la 2-esfera, no es posible parametrizar todo el espacio con una única elección de las coordenadas (en la 2-esfera, al menos un meridiano que va del polo norte al polo sur queda sin parametrizar), para ello se tendrían que coger otros rangos que cubran las partes sin parametrizar. Nótese también que para cualquier valor fijo de ψ, θ y φ parametrizan una 2-esfera de radio sin(ψ).
El tensor métrico sobre la 3-esfera en estas coordenadas está determinado por
y la forma de volumen por
Estas coordenadas pueden ser descritas en términos de cuaterniones. Cualquier cuaternión unidad q puede escribirse de la forma:
donde τ es un cuaternión imaginario unidad (es decir, cualquier cuaternión que satisface τ2 = −1). Este es el análogo cuaterniónico de la fórmula de Euler. Ahora los cuaterniones imaginarios unidad yacen todos sobre la 2-esfera unidad en Im H, de modo que cualquier τ puede escribirse como:
Con τ de esta forma, el cuaternión unidad q está dado por
donde las x son como se indica más arriba.
Cuando se usa q para describir rotaciones espaciales (cf. cuaterniones y rotación espacial) describe una rotación alrededor de τ a través de un ángulo de 2ψ.
Coordenadas de Hopf
Otra elección de coordenadas hiperesféricas, (η, ξ1, ξ2), usa el encaje de S3 en C2. En coordenadas complejas (z1, z2) ∈ C2 escribiremos
Aquí η se desplaza en el rango 0 a π/2, y ξ1 y ξ2 pueden tomar cualquier valor entre 0 y 2π. Estas coordenadas son útiles en la descripción de la 3-esfera como un haz de Hopf
Para cualquier valor de η entre 0 y π/2, las coordenadas (ξ1, ξ2) parametrizan un toro bidimensional. En los caso degenerados, cuando η es igual a 0 o a π/2, estas coordenadas describen un círculo.
El tensor métrico sobre la 3-esfera en estas coordenadas está dado por
y la forma de volumen por
Coordenadas estereográficas
Otra conjunto de coordenadas conveniente puede obtenerse por proyección estereográfica de S3 sobre un hiperplano de R3 tangente. Por ejemplo, si proyectamos sobre el plano tangente al punto (1, 0, 0, 0) se podría escribir un punto p en S3 como
donde u = (u1, u2, u3) es un vector en R3 y ||u||2 = u12 + u22 + u32. En la segunda igualdad de arriba hemos identificado p con un cuaternión unidad y u = u1 i + u2 j +u3 k con un cuaternión puro. (Nótese que aquí la división está bien definida, aún cuando la multiplicación cuaterniiónica es generalmente no conmutativa). La inversa de este mapa transforma p = (x0, x1, x2, x3) en S3 en
Bien podríamos haber proyectado sobre el plano tangente al punto (−1, 0, 0, 0), en cuyo caso el punto p estaría dado por
donde v = (v1, v2, v3) es un vector en el segundo R3. La inversa de este mapa transforma p en
Nótese que las coordenadas u están definidas en todas partes excepto (−1, 0, 0, 0) y las coordenadas v en todas partes excepto (1, 0, 0, 0). Ambos "parches" juntos cubren la totalidad S3. Esto define un atlas sobre S3 que consiste de dos cartas coordinadas. Nótese también que la función de transición entre estas dos cartas en su superposición está dada por
y viceversa.
Tangentes
Una 3-esfera unidad embebida en el 4-espacio tiene un 3-espacio de vectores tangentes, TpS3, en cualquier punto p. Si (x0,x1,x2,x3) son las coordenadas de p, entonces el vector con coordenadas (−x1,x0,−x3,x2) está en TpS3, y la colección de todos esos vectores forma un campo continuo de vectores unidad en S3. (Esta es una seccióndel haz de tangentes, TS3.) Tal construcción claramente es posible para esferas en todos los espacios con un número par de dimensiones, S2n−1; pero una implicación del teorema de índices de Atiyah-Singer es que resulta imposible para S2n (para n positivo).
n-esferas
Véase también: n-esfera
Se puede generalizar la noción de esfera en espacios vectoriales de dimensiones superiores a tres. A partir de la cuarta dimensión ya no es representable gráficamente, pero la definición sigue siendo que la esfera es el conjunto de los puntos equidistantes de un punto fijo. En un espacio euclídeo de n+1 dimensiones, usando coordenas cartesianas, la ecuación de una n-esfera:
Y para una esfera de radio r, y centro (c1, c2, ..., cn):
El volumen de la bola contenida en la superficie cerrada anterior, en dimensión n se calcula por inducción sobre n. Aquí están los diez primeros valores de Vn(r) y las superficies correspondientes:
| Dimensión | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | n |
| Volumen | 2r | πr² | 4πr³ 3 | π²r4 2 | 8π²r5 15 | π³r6 6 | 16π³r7 105 | π4r8 24 | 32π4r9 945 | π5r10 120 | πn/2rn Γ(n/2+1) |
| Superficie | 2 | 2πr | 4πr² | 2π²r³ | 8π²r4 3 | π³r5 | 16π³r6 15 | π4r7 3 | 32π4r8 105 | π5r9 12 | nπn/2rn-1 Γ(n/2+1) |
El volumen de la bola alcanza su máximo en dimensión 5, mientras que la superficie de la esfera lo alcanza en dimensión 7.
Existe la posibilidad de representar una n-esfera o hiperesfera de n dimensiones como fibrado de otra hiperesfera de dimensión inferior. Esto sólo sucede en tres casos:
 , puede ser representada como fibrado no trivial con espacio base
, puede ser representada como fibrado no trivial con espacio base  y fibra
y fibra  , esta construcción puede obtenerse a partir de una construcción geométrico-algebraica utilizando números complejos.
, esta construcción puede obtenerse a partir de una construcción geométrico-algebraica utilizando números complejos.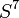 , puede ser representada como fibrado no trivial con espacio base
, puede ser representada como fibrado no trivial con espacio base 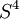 y fibra
y fibra  , esta construcción puede obtenerse a partir de una construcción geométrico-algebraica utilizando números cuaterniónicos.
, esta construcción puede obtenerse a partir de una construcción geométrico-algebraica utilizando números cuaterniónicos. , puede ser representada como fibrado no trivial con espacio base
, puede ser representada como fibrado no trivial con espacio base  y fibra
y fibra 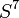 , esta construcción puede obtenerse a partir de una construcción geométrico-algebraica utilizando números octoniónicos.
, esta construcción puede obtenerse a partir de una construcción geométrico-algebraica utilizando números octoniónicos.
Para dimensión superior no existen otros casos en que esto sea posible.2
En literatura
Stephen Baxter usó la 3-esfera en su cuento Dante and the 3-Sphere, una historia en la que un científico y teólogo aparentemente loco "se da cuenta" de que Dante en la "Divina Comedia" se refiere a una transversal a través de múltiples 3-esferas. El personaje principal es llevado por el científico a un viaje a través de múltiples 3-esferas.
En Flatland de Edwin Abbott Abbott, publicado en 1884, se hace referencia a las 3-esferas como sobresferas.






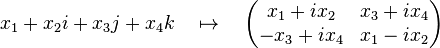
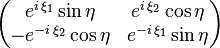
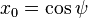



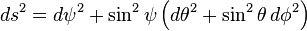







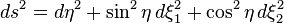




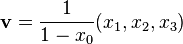



No hay comentarios:
Publicar un comentario