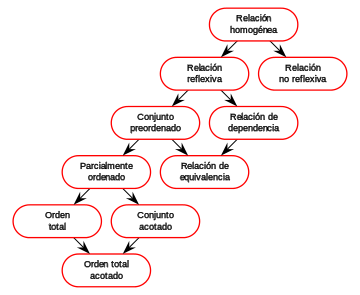
Acotado
acotado aparece en matemáticas para referirse a una situación en la que para cierto objeto matemático o un objeto construido a partir del mismo puede establecerse una relación de orden con otro tipo de entidad llamada cota superior o inferior. Los detalles varían según el contexto por lo que se remite al cuerpo de este artículo para una definición precisa en cada caso.
Conjunto parcialmente ordenado y acotado
Dado un conjunto A y una relación binaria  definida entre los elementos de A, que expresaremos
definida entre los elementos de A, que expresaremos  y la relación se representa:
y la relación se representa:
 definida entre los elementos de A, que expresaremos
definida entre los elementos de A, que expresaremos  y la relación se representa:
y la relación se representa:
que se lee: x antecede a y.
La no relación se representa:
que se lee: x no antecede a y
Si la relación  cumple las propiedades: reflexiva, antisimétrica y transitiva, es por lo tanto es un conjunto parcialmente ordenado.
cumple las propiedades: reflexiva, antisimétrica y transitiva, es por lo tanto es un conjunto parcialmente ordenado.
 cumple las propiedades: reflexiva, antisimétrica y transitiva, es por lo tanto es un conjunto parcialmente ordenado.
cumple las propiedades: reflexiva, antisimétrica y transitiva, es por lo tanto es un conjunto parcialmente ordenado.
Si se cumple que:
el elemento x antecede a y o y antecede a x, se dice que x y y son elementos comparables.
Si se cumple que:
el elemento x no antecede a y e y no antecede a x, se dice que x e y son no comparables.
Diremos que el conjunto A está acotado superiormente respecto a  si:
si:
 si:
si:
para todo x de A se cumple que existe un y de A tal que x antecede a y.
Del mismo modo diremos que el conjunto A está acotado inferiormente respecto a  si:
si:
 si:
si:
para todo x de A se cumple que existe un z de A tal que z antecede a x.
Diremos que un conjunto está acotado, si está acotado superior e inferiormente.
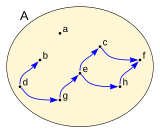
Elemento maximal y minimal
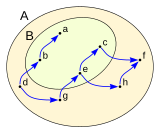
Dado el conjunto A formado por los elementos:
en el que se ha definido una relación binaria  representada en la figura, siendo
representada en la figura, siendo  un conjunto parcialmente ordenado, los elementos y de A que cumplen:
un conjunto parcialmente ordenado, los elementos y de A que cumplen:
 representada en la figura, siendo
representada en la figura, siendo  un conjunto parcialmente ordenado, los elementos y de A que cumplen:
un conjunto parcialmente ordenado, los elementos y de A que cumplen:
y de A es maximal si para todo x de A que cumple que y anteceda a x entonces y es igual a x.
Los elementos yde A se denominan maximales y definen una cuota superior en A, los elementos maximales no tiene porque ser únicos, en el ejemplo b, a y f son maximales de A.
Del mismo modo los elementos z de A que cumplen:
z de A es minimal si para todo x de A que cumpla que x anteceda a z entonces z es igual a x.
se denominan minimales y definen una cuota inferior en A, los elementos minimales no tiene porque ser únicos, en el ejemplo d, a y c son minimales de A.
Se puede ver que el elemento a es maximal y minimal en A
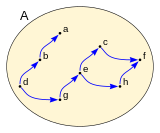
Elemento máximo y mínimo
Dado el conjunto A formado por los elementos:
en el que se ha definido una relación binaria  representada en la figura, siendo
representada en la figura, siendo  un conjunto parcialmente ordenado.
un conjunto parcialmente ordenado.
 representada en la figura, siendo
representada en la figura, siendo  un conjunto parcialmente ordenado.
un conjunto parcialmente ordenado.
El elemento y de A que cumple:
se denomina máximo y define una cuota superior en A, el elemento máximo es único, en el ejemplo f es el máximo de A. El elemento máximo de un conjunto es maximal en ese conjunto.
Del mismo modo el elemento z de A que cumple:
se denomina mínimo y define una cuota inferior en A, el elemento mínimo es único, en el ejemplo d es mínimo de A. El elemento mínimo de un conjunto es minimal en ese conjunto.
Galería de ejemplos
Dado un conjunto A, entre cuyos elementos, se ha definido una relación binaria que define un orden parcial, definido en las siguientes figuras, se pueden ver los distintos casos para determinar los maximales, minimales, maximos y minimos de cada caso en caso de existir:
Conjunto con orden total y acotado
Dado un conjunto A y una relación binaria  definida entre los elementos de A, que expresaremos
definida entre los elementos de A, que expresaremos  y la relación se representa:
y la relación se representa:
 definida entre los elementos de A, que expresaremos
definida entre los elementos de A, que expresaremos  y la relación se representa:
y la relación se representa:
que se lee: a antecede a b.
Si la relación  cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
 cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
Se cumple que:
todos los elementos de un conjunto con orden total son comparables.
Dado el conjunto A formado por los elementos:
en el que se ha definido una relación binaria  representada en la figura, siendo
representada en la figura, siendo  un conjunto totalmente ordenado.
un conjunto totalmente ordenado.
 representada en la figura, siendo
representada en la figura, siendo  un conjunto totalmente ordenado.
un conjunto totalmente ordenado.
El elemento y de A que cumple:
se denomina máximo y define una cuota superior en A, el elemento máximo es únicos, en el ejemplo e es el máximo de A.
Del mismo modo el elemento z de A que cumple:
se denomina mínimo y define una cuota inferior en A, el elemento mínimo es únicos, en el ejemplo a mínimo de A.
Conjunto de los números naturales
Dado el conjunto N de los números naturales y una relación binaria menor o igual:  definida entre los números naturales, que expresaremos
definida entre los números naturales, que expresaremos  y la relación se representa:
y la relación se representa:
 definida entre los números naturales, que expresaremos
definida entre los números naturales, que expresaremos  y la relación se representa:
y la relación se representa:
que se lee: a es menor o igual que b.
La relación  cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
 cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
Se cumple que:
para todo: a, b número natural: a es menor o igual que b o b es menor o igual que a, todos los números naturales son comparables.
Dado el conjunto N formado por los elementos:
en el que se ha definido una relación binaria  representada en la figura, siendo
representada en la figura, siendo  un conjunto totalmente ordenado.
un conjunto totalmente ordenado.
 representada en la figura, siendo
representada en la figura, siendo  un conjunto totalmente ordenado.
un conjunto totalmente ordenado.
No existe el elemento y de N que cumple:
Este elemento seria el máximo en N y definiría una cuota superior en N, el conjunto de los números naturales no tiene cuota superior.
El elemento z de N que cumple:
se denomina mínimo y define una cuota inferior en N, el elemento mínimo es únicos, el uno:1 es el mínimo de N.
Conjunto de los números enteros
Dado el conjunto Z de los números enteros y una relación binaria menor o igual:  definida entre los números enteros, que expresaremos
definida entre los números enteros, que expresaremos  y la relación se representa:
y la relación se representa:
 definida entre los números enteros, que expresaremos
definida entre los números enteros, que expresaremos  y la relación se representa:
y la relación se representa:
que se lee: a es menor o igual que b.
La relación  cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
 cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total.
Se cumple que:
para todo: a, b número entero: a es menor o igual que b o b es menor o igual que a, todos los números enteros son comparables.
Dado el conjunto Z formado por los elementos:
en el que se ha definido una relación binaria  representada en la figura, siendo
representada en la figura, siendo  un conjunto totalmente ordenado.
un conjunto totalmente ordenado.
 representada en la figura, siendo
representada en la figura, siendo  un conjunto totalmente ordenado.
un conjunto totalmente ordenado.
No existe el elemento y de Z que cumple:
Este elemento seria el máximo en Z y definiría una cuota superior en Z, el conjunto de los números enteros no tiene cuota superior.
No existe el elemento z de Z que cumple:
Este elemento seria mínimo y definiría una cuota inferior en Z, el conjunto de los números enteros no tiene cuota inferior respecto a la relación binaria:  .
.
 .
.Subconjunto de un conjunto parcialmente ordenado
Partiendo de un conjunto:
en el que se ha definido, entre los elementos del conjunto, una relación binaria:  que representamos
que representamos  y la relación entre elementos:
y la relación entre elementos:
 que representamos
que representamos  y la relación entre elementos:
y la relación entre elementos:
que se lee: x antecede a y.
Que cumple las propiedades: reflexiva, antisimetrica y transitiva, por lo que se define en el conjunto, respecto a la relación binaria, un orden parcial. Siendo B un subconjunto de A:
se puede determinar si B está acotado según los siguientes conceptos:
- Mayorante: es todo elemento de A que anteceda a todo elemento de B.
- Supremo: es el elemento mayorante que es antecedido por todos los elemento mayorantes.
- Mayor: es el nombre que recibe el supremo, en caso de existir, y ser un elemento de B.
- Minorante: es todo elemento de A que es antecedido por todo elemnto de B.
- Ínfimo: es el elemento minorante que antecede a todos los elementos minorantes.
- Menor: es el nombre que recibe el ínfimo, en caso de existir, y ser un elemento de B.
Galería de ejemplos
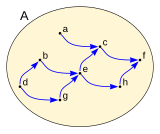
Dado un conjunto A:
en el que se ha dedinidi una relación binaria  entre los elementos de A que define un orden parcial, y siendo B en subconjunto de A, definido:
entre los elementos de A que define un orden parcial, y siendo B en subconjunto de A, definido:
 entre los elementos de A que define un orden parcial, y siendo B en subconjunto de A, definido:
entre los elementos de A que define un orden parcial, y siendo B en subconjunto de A, definido:
Podemos ver una galería de ejemplo, que permiten discernir: mayorante, supremo y mayor así como: minorante, infimo y menor.
Subconjunto de un conjunto con orden total
Dado un conjunto  :
:
 :
:
en el que se ha definido, entre los elementos del conjunto, una relación binaria:  que representamos
que representamos  y la relación entre elementos:
y la relación entre elementos:
 que representamos
que representamos  y la relación entre elementos:
y la relación entre elementos:
que se lee: a antecede a b.
Que cumple las propiedades: reflexiva, antisimetrica, transitiva y total, por lo que se define en el conjunto, respecto a la relación binaria, un orden total.
Siendo B:
un subconjunto de A, se puede determinar en B: mayorantes, supremo y mayor, así como: minorantes, infimo y menor:
- Mayorantes: d, e
- Supremo: d
- Mayor: d
- Minorantes: a, b
- Infimo: b
- Menor: b
Subconjunto de los números enteros
Dado el conjunto Z de los enteros y una relación binaria menor o igual:  definida entre los enteros, que expresaremos
definida entre los enteros, que expresaremos  y la relación se representa:
y la relación se representa:
 definida entre los enteros, que expresaremos
definida entre los enteros, que expresaremos  y la relación se representa:
y la relación se representa:
que se lee: siendo x, y números enteros: x es menor o igual que y.
La relación  cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total. Todos los números enteros soncomparables respecto a
cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total. Todos los números enteros soncomparables respecto a  .
.
 cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total. Todos los números enteros soncomparables respecto a
cumple las propiedades reflexiva, antisimétrica, transitiva y total, es por lo tanto es un conjunto con orden total. Todos los números enteros soncomparables respecto a  .
.
Dado un subconjunto de Z:
podemos ver que:
Intervalos de números reales
Dado el conjunto R de los números reales y una relación binaria menor o igual:  definida entre los reales que expresaremos
definida entre los reales que expresaremos  y la relación se representa:
y la relación se representa:
 definida entre los reales que expresaremos
definida entre los reales que expresaremos  y la relación se representa:
y la relación se representa:
y se lee: siendo x, y números reales: x es menor o igual que y.
La relación  cumple las propiedades: reflexiva, antisimétrica, transitiva y total, que define un conjunto con orden total. Todos los números reales son comparables respecto a
cumple las propiedades: reflexiva, antisimétrica, transitiva y total, que define un conjunto con orden total. Todos los números reales son comparables respecto a  .
.
 cumple las propiedades: reflexiva, antisimétrica, transitiva y total, que define un conjunto con orden total. Todos los números reales son comparables respecto a
cumple las propiedades: reflexiva, antisimétrica, transitiva y total, que define un conjunto con orden total. Todos los números reales son comparables respecto a  .
.
Considerando un intervalo un subconjunto conexo de los números real, es decir, una parte de recta entre dos valores dados.
Intervalo cerrado
Dado el intervalo cerrado de números reales:
que se define:
Se puede ver que:
Intervalo abierto
Dado el intervalo abierto de números reales:
que se define:
Se puede ver que:
Intervalo infinito
Dado el intervalo abierto de números reales:
que se define:
Se puede ver que:
Conjunto acotado en un espacio métrico
Sean M un espacio métrico y A un subconjunto de M. Se dice que A está acotado si existe algún disco cerrado que lo contenga.
Conjunto acotado en el conjunto de los números reales
Sean A un subconjunto de números reales y M un número real positivo. Se dice que A es acotado si existe un M tal que para todo x ∈ A se verifica que |x| es menor o igual que M.
Conjunto acotado superiormente
Un conjunto  completamente ordenado está acotado superiormente si existe un elemento
completamente ordenado está acotado superiormente si existe un elemento  que sea mayor que cualquier elemento del conjunto, es decir:
que sea mayor que cualquier elemento del conjunto, es decir:
 completamente ordenado está acotado superiormente si existe un elemento
completamente ordenado está acotado superiormente si existe un elemento  que sea mayor que cualquier elemento del conjunto, es decir:
que sea mayor que cualquier elemento del conjunto, es decir:(*)
Nótese que con esta definición puede ser que  o que
o que  . A cualquier número
. A cualquier número  que satisfaga () se le llamacota superior.
que satisfaga () se le llamacota superior.
 o que
o que  . A cualquier número
. A cualquier número  que satisfaga () se le llamacota superior.
que satisfaga () se le llamacota superior.
Si un conjunto está acotado superiormente en general existirá más de una cota superior, denotando al conjunto de cotas superiores de  como
como  se define el supremode
se define el supremode  como el mínimo de este conjunto:
como el mínimo de este conjunto:
 como
como  se define el supremode
se define el supremode  como el mínimo de este conjunto:
como el mínimo de este conjunto:
Si  está acotado entonces tiene un supremo. Si resulta que
está acotado entonces tiene un supremo. Si resulta que  entonces el supremo resulta además ser un máximo del conjunto
entonces el supremo resulta además ser un máximo del conjunto  .
.
 está acotado entonces tiene un supremo. Si resulta que
está acotado entonces tiene un supremo. Si resulta que  entonces el supremo resulta además ser un máximo del conjunto
entonces el supremo resulta además ser un máximo del conjunto  .
.Conjunto acotado inferiormente
Sea A un subconjunto no vacío de números reales, se dice que A es acotado inferiormente si existe k que pertenece a los reales tal que k < x o k = x para todo x que pertenece a A. El número k se denomina cota inferior para A pues los números menores que k también son cotas inferiores, lo cual indica que el conjunto de todas las cotas inferiores de A es infinito.
Ejemplos
- El conjunto de números enteros positivos consta de un ínfimo, el 0, por lo que es un Conjunto Acotado Inferiormente.
- El conjunto de los números enteros negativos consta de un supremo, el 0, por lo que es un Conjunto Acotado Superiormente.
- Un conjunto que conste de los números {-3, 0, 1, 5, 32, 120} consta de una mayorante (el 120), una minorante (el -3) y un subconjunto que consta de los cuatro elementos restantes, por lo que es un Conjunto Acotado.
Función acotada en un dominio D
Una función matemática f se llama función acotada en un dominio D (conjunto abierto conexo no vacío) cuando el conjunto imagen o recorrido de la función es un conjunto acotado, es decir, cuando la función solo existe para un intervalo numérico determinado. Por esta misma razón si una función solo existe en un intervalo numérico concreto se le llama "función acotada" ya que su resultado está limitado (acotado) a unos valores numéricos concretos que son finitos . Por ejemplo, las funciones trigonométricas  y
y  , para las cuales
, para las cuales ![f(D) =[-1,+1]\,](https://upload.wikimedia.org/math/e/f/f/eff7fe83f1549bea026565ec5d73ddd0.png) , son funciones acotadas ya que todos sus posibles resultados están contenidos en un intervalo numérico acotado, en este caso el intervalo cerrado [-1,1].
, son funciones acotadas ya que todos sus posibles resultados están contenidos en un intervalo numérico acotado, en este caso el intervalo cerrado [-1,1].
 y
y  , para las cuales
, para las cuales ![f(D) =[-1,+1]\,](https://upload.wikimedia.org/math/e/f/f/eff7fe83f1549bea026565ec5d73ddd0.png) , son funciones acotadas ya que todos sus posibles resultados están contenidos en un intervalo numérico acotado, en este caso el intervalo cerrado [-1,1].
, son funciones acotadas ya que todos sus posibles resultados están contenidos en un intervalo numérico acotado, en este caso el intervalo cerrado [-1,1].Función acotada superiormente en un dominio D
Dada una función  , se dice que tiene una cota superior o que está acotada superiormente si existe un valor
, se dice que tiene una cota superior o que está acotada superiormente si existe un valor  tal que
tal que  para cualquier valor de x perteneciente al dominio D. K se llama cota superior de
para cualquier valor de x perteneciente al dominio D. K se llama cota superior de  en D.
en D.
 , se dice que tiene una cota superior o que está acotada superiormente si existe un valor
, se dice que tiene una cota superior o que está acotada superiormente si existe un valor  tal que
tal que  para cualquier valor de x perteneciente al dominio D. K se llama cota superior de
para cualquier valor de x perteneciente al dominio D. K se llama cota superior de  en D.
en D.
Dicho formalmente:  es acotada superiormente si
es acotada superiormente si 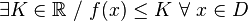 .
.
 es acotada superiormente si
es acotada superiormente si 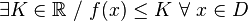 .
.Función acotada inferiormente en un dominio D
Dada una función  , se dice que tiene una cota inferior o que está acotada inferiormente si existe un valor K tal que
, se dice que tiene una cota inferior o que está acotada inferiormente si existe un valor K tal que  para cualquier valor de xperteneciente al dominio D. K se llama cota inferior de
para cualquier valor de xperteneciente al dominio D. K se llama cota inferior de  en D.
en D.
 , se dice que tiene una cota inferior o que está acotada inferiormente si existe un valor K tal que
, se dice que tiene una cota inferior o que está acotada inferiormente si existe un valor K tal que  para cualquier valor de xperteneciente al dominio D. K se llama cota inferior de
para cualquier valor de xperteneciente al dominio D. K se llama cota inferior de  en D.
en D.Ejemplos
- La función
 (parábola) es una función acotada inferiormente en el eje real con cota igual a 0.
(parábola) es una función acotada inferiormente en el eje real con cota igual a 0. - La función
 (parábola invertida) es una función acotada superiormente en el eje real con cota igual a 0.
(parábola invertida) es una función acotada superiormente en el eje real con cota igual a 0. - La función
 (función seno) es una función acotada en el eje real, con cota inferior igual a -1 y cota superior igual a 1.
(función seno) es una función acotada en el eje real, con cota inferior igual a -1 y cota superior igual a 1. - La función
 (la circunferencia unitaria) en el dominio D = {
(la circunferencia unitaria) en el dominio D = { } tiene una cota superior igual a 2 y una cota inferior igual a 0.
} tiene una cota superior igual a 2 y una cota inferior igual a 0.
Operador acotado
En un espacio de Hilbert (o un espacio de Banach) un operador acotado es aquel que tiene una norma máxima definida sobre la bola unidad. Por tanto para un operador acotado se cumple que:
Algunos operadores importantes de la mecánica cuántica como el hamiltoniano suelen ser no acotados, lo cual tiene cierta significación física ya que en general la mayoría de sistemas físicos no tienen un límite superior de la energía que pueden contener.
Segmento acotado
En un croquis, se llama segmento acotado aquél que está limitado por ambos extremos con sus dimensiones indicadas.
Croquis acotado
Representación de un objeto en un plano horizontal o vertical con indicación de las dimensiones del objeto.
Término no acotado
En matemáticas el término no acotado se refiere a alguna entidad matemática infinita o para la cual no es posible establecer una cota máxima para alguna de sus propiedades o medidas.
Conjuntos no acotados
Dentro de un espacio métrico (E, d) un conjunto no acotado es un conjunto infinito tal que tiene puntos situados a distancia infinita, es decir, no existe ningún valor  tal que:
tal que:
 tal que:
tal que:
Alternativamente un conjunto no acotado es aquel que no cabe dentro de ninguna bola de radio finito de dicho espacio métrico.
Operador no acotado
Fijado un espacio vectorial normado, un operador A se dice no acotado o discontinuo si no existe  tal que:
tal que:
 tal que:
tal que:
Conjunto acotado
Descripción:Un conjunto es acotado si existe una bola que lo contenga, es decir, y tales queDescriptores:TopologíaÁlgebraEjemplo:El conjunto definido por es un conjunto acotado.Si consideramos la Bola de centro en el punto y de radio r=3, se tiene que .Es decir, el conjunto es acotado












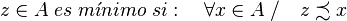













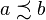
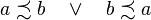
































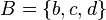








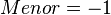

![I = [a,b]\](https://upload.wikimedia.org/math/5/a/6/5a6aef6ce626a63d1e3c1cfb17e1a97e.png)
![I = [a,b]
\; , \quad
\forall x \in R
\; : \quad
a \le x \le b](https://upload.wikimedia.org/math/e/6/5/e658fce67aeef1e9498d97ef9b667a1a.png)



















No hay comentarios:
Publicar un comentario