sábado, 14 de noviembre de 2015

Electromagnetísmo

Electrodinámica cuántica

La electrodinámica cuántica (QED acrónimo en inglés de Quantum Electrodynamics) es la teoría cuántica del campo electromagnético. QED describe los fenómenos que implican las partículas eléctricamente cargadas que obran recíprocamente por medio de la fuerza electromagnética.

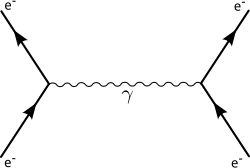
Diagrama de Feynman ilustrando la interacción entre dos electrones producida mediante el intercambio de un fotón. Este tipo de diagramas son importantes guiar los cálculos dentro de QED.

Historia y predicciones

Feynman (centro), uno de los creadores de la QED, en Los Alamos.
La QED es una de las teorías más precisas de cuantas que se crearon en el siglo XX. Es capaz de hacer predicciones de ciertas magnitudes físicas con hasta veinte cifras decimales de precisión, un resultado poco frecuente en las teorías físicas anteriores. Por esa razón la teoría fue llamada "la joya de la física". Entre sus predicciones más exactas están:
c\; es la velocidad de la luz en el vacío.
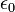\epsilon_0\; es la permitividad eléctrica del vacío.
Shin'ichirō Tomonaga, Julian Schwinger y Richard Feynman recibieron los premios Nobel de Física de 1965 por su desarrollo, sus contribuciones que implicaban una prescripción covariante y gauge invariante para el cálculo de cantidades observables. La técnica matemática de Feynman, basada en sus diagramas, parecía inicialmente muy diferente del enfoque teórico de campos, basado en operadores de Schwinger y Tomonaga, pero fue más adelante demostrado como equivalente. El procedimiento de renormalización para dar sentido a algunas de las predicciones infinitas de la teoría cuántica del campo también encontró su primera puesta en práctica acertada en electrodinámica cuántica.

Descripción de la teoría

La electrodinámica cuántica es una descripción detallada de la interacción entre fotones y partículas cargadas de tipo fermiónico. La teoría cuántica comparte ciertos rasgos con la descripción clásica. De acuerdo con la descripción de la óptica clásica la luz viaja sobre todos los caminos permitidos, y su interferencia determina losfrentes de onda que se propagan de acuerdo con el principio de Fermat. Similarmente, en la descripción cuántica de los fotones (y los fermiones), estos pasan por cada camino posible permitido por aberturas o sistemas ópticos. En ambos casos el observador detecta simplemente el resultado matemático de la superposición de todas las ondas consideradas a lo largo de integrales de línea. Una diferencia es que en la electrodinámica la velocidad efectiva de un fotón puede superar la velocidad de la luzen promedio.1
Además QED fue la primera teoría cuántica del campo en la cual las dificultades para construir una descripción completa de campos y de creación y aniquilación de partículas cuánticas, fueron resueltas satisfactoriamente.

Formalismo

Diagramas de Feynman simples usados para los cálculos perturbativos de QED.
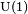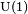Matemáticamente, podemos decir que la electrodinámica cuántica tiene la estructura de una teoría de gauge abeliana, siendo el grupo de gauge asociado en grupo unitario \scriptstyle \mathrm{U}(1). El campo de gauge que media la interacción entre campos de espín -1/2 con carga es el campo electromagnético.
La evolución temporal de un sistema de partículas cargadas y fotones puede ser calculada mediante un cálculo perturbativo. En concreto la comparación con los experimentos realizables frecuentemente requiere el cálculo de los elementos de lamatriz S que permiten encontrar las secciones eficaces de dispersión para partícula que puede ser comparada con los resultados de los experimentos.
La electrodinámica cuántica reduce este tipo de cálculos a un desarrollo perturbativo en serie de potencias que permite encontrar con la precisión deseada esas secciones eficaces. Cada uno de los términos perturbativos admite una representación gráfica conocida como diagrama de Feynman. De hecho, la electrodinámica cuántica fue históricamente la primera teoría donde se usaron diagramas de Feynman como ayuda en el cálculo perturbativo. La forma de cada uno de los términos perturbativos y, por tanto, la representación gráfica asociada depende de la forma del lagrangiano que caracteriza dicha teoría (ver más adelante).

La invarianza gauge local \mathrm{U}(1)

Véase también: Teoría de gauge
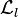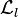Es interesante observar como se puede hallar el lagrangiano de la QED como simple exigencia de que el lagrangiano de un fermión libre con carga eléctrica no nula seainvariante gauge local. Sea \mathcal{L}_l el lagrangiano del fermión libre:
\mathcal{L}_l=\dot{\imath}\bar{\psi}\gamma^{\mu}\partial_{\mu}\psi - m\bar{\psi}\psi=\bar{\psi}(\dot{\imath}\gamma^{\mu}\partial_{\mu} -m)\psi
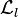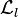En otras palabras, queremos que \mathcal{L}_l sea invariante bajo una transformación local \mathrm{U}(1) de manera que el campo cambie como:
\psi(x)\rightarrow e^{-\dot{\imath}\alpha (x)}\psi(x)
En ese caso, la derivada covariante y el gauge serán:
D_{\mu}=\partial_{\mu}-\dot{\imath}eA_{\mu}\qquad \therefore\qquad A_{\mu}\rightarrow A_{\mu}-\frac{1}{e}\partial_{\mu}\alpha.
Con todo esto, nos queda el lagrangiano de la electrodinámica cuántica:
\mathcal{L}_{QED}=\bar{\psi}\left( \dot{\imath}\gamma^{\mu}\partial_{\mu}-m\right)\psi +e\bar{\psi}\gamma^{\mu}A_{\mu}\psi-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}.

Adecuación experimental

Es importante señalar que la electrodinámica cuántica no da valores concretos de lo que sucedería en un experimento concreto, sino sólo probabilidades de que suceda un determinado tipo de situación. Es por eso, que los experimentos usan un número relativamente grande de partículas que son dispersadas estadísticamente de acuerdo con las probabilidades predichas por la teoría. A partir de la distribución de partículas dispersadas puede medirse la sección eficaz comparable con las predicciones numéricas de la teoría.
Las predicciones de la electrodinámica cuántica han sido confirmadas por los experimentos hasta un nivel insólito de precisión: habitualmente se tienen experimentos que coinciden en 12 cifras decimales correctas con las predicciones de la teoría. Esto hace de la electrodinámica cuántica la teoría más precisa construida por el hombre.

Formulación matemática

La dinámica y propiedades básicas de una teoría de campo depende de la forma seleccionada para el lagrangiano. La selección de lagrangiano depende de las simetrías del grupo de gauge y del hecho de que la teoría describa adecuadamente la interacción entre fermiones cargados. En una teoría que describa campos fermiónicos interactuando mediante un campo de gauge bosónico asociado a partículas sin masa (fotones) cuyo grupo de gauge es conmutativo, el lagrangiano de partida puede tomarse como:
(1)\mathcal{L} = i \bar{\psi} \gamma^\mu \partial_\mu \psi - e\bar{\psi}\gamma_\mu A^\mu \psi -m \bar{\psi} \psi - \frac{1}{4}F_{\mu\nu}F^{\mu\nu}\,
Donde el campo ferminónico \ \psi y su adjunto de Dirac \bar\psi son los campos que representan partículas de carga eléctrica, específicamente el electrón y los campos del positrón representados como espinor de Dirac. La parte del lagrangiano que contiene el tensor de campo electromagnético describe la evolución libre del campo electromagnético, mientras que la ecuación de Dirac con la derivada covariante de gauge describe la evolución libre de los campos del electrón y del positrón así como su interacción con el campo electromagnético.

Ecuaciones de movimiento

Las ecuaciones de "movimiento" o ecuaciones de evolución temporal de la QED pueden obtenerse mediante las ecuaciones de Euler-Lagrange del lagrangiano de la teoría. Insertando ese lagrangiano en las ecuaciones de Euler-Lagrange se obtiene la ecuación de evolución temporal de la teoría:
(2) \partial_\mu \left( \frac{\partial \mathcal{L}}{\partial ( \partial_\mu \psi )} \right) - \frac{\partial \mathcal{L}}{\partial \psi} = 0 \quad \mbox{con} \begin{cases} \partial_\mu \left( \frac{\partial \mathcal{L}}{\partial ( \partial_\mu \psi )} \right) = \partial_\mu \left( i \bar{\psi} \gamma^\mu \right)\\ \frac{\partial \mathcal{L}}{\partial \psi} = -e\bar{\psi}\gamma_\mu A^\mu - m \bar{\psi} \end{cases}
Colocando los dos términos dentro de la ecuación de Euler-Lagrange resulta finalmente la siguiente ecuación de evolución para el campo fermiónico:
i \gamma^\mu \partial_\mu \psi - m \psi = e \gamma_\mu A^\mu \psi \,
El miembro de la izquierda es precisamente la ecuación de Dirac y el término de la derecha representa la interacción con el campo electromagnético.
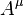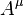Las mismas ecuaciones de Euler-Lagrange, aplicadas ahora al campo A^\mu, permiten encontrar las ecuaciones de evolución del campo electromagnético:
(3) \part_\nu \left( \frac{\part \mathcal{L}}{\part ( \part_\nu A_\mu )} \right) - \frac{\part \mathcal{L}}{\part A_\mu} = 0 \quad \mbox{con} \begin{cases} \part_\nu \left( \frac{\part \mathcal{L}}{\part ( \part_\nu A_\mu )} \right) = \part_\nu \left( \part^\mu A^\nu - \part^\nu A^\mu \right)\\ \frac{\part \mathcal{L}}{\part A_\mu} = -e\bar{\psi} \gamma^\mu \psi \end{cases}
Y la ecuación de evolución del campo electromagnético resulta finalmente:
\partial_\nu F^{\nu \mu} = e \bar{\psi} \gamma^\mu \psi \,
Donde el segundo miembro puede ser interpretado como la densidad de corriente asociada al campo fermiónico.

Reglas de Feynman

Para dar cuenta de todos los efectos cuánticos, es necesario reemplazar las componentes de los campos en las anteriores ecuaciones diferenciales por operadores autoadjuntos interpretables como genuinos operadores cuánticos. 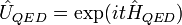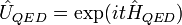En general eso lleva a unos sistemas de ecuaciones que no sabemos como integrar exactamente, pero que admiten un tratamiento perturbativo, descomponiendo el operador de evolución temporal \hat{U}_{QED}=\exp(it\hat{H}_{QED}) en series de potencias o serie perturbativa.
El cálculo de cada término de la serie anterior puede realizarse de manera casi automática con la ayuda de los llamados diagramas de Feynman, a los que se puede asociar unas reglas de Feynman. La precisión del cálculo depende de cuantos términos se consideran en la serie perturbativa anterior.

Renormalización

Un serio problema con las reglas de Feynman es que tal que fueron establecidas por primera vez conducen a diagramas y términos divergentes en la serie perturbativa, es decir, términos no finitos que echan a perder el cálculo de los términos finitos. Obviamente todos los resultados físicos son finitos y esos términos divergentes del cálculo no son observables en la realidad. La renormalización es un conjunto de reglas adicionales que interpretan qué relación existe entre los términos calculados y los términos medibles en la realidad y generan reglas adicionales que permiten "normalizar" los cálculos y garantizar que se producen resultados numéricos finitos comparables con la realidad mediante experimento.
Es conocido que el hecho de que una teoría cuántica sea una teoría de campo de gauge le confiere la propiedad de ser renormalizable, en el sentido de que existe un conjunto de reglas adicionales que permiten eliminar términos divergentes no observables y dar lugar a resultados finitos.

Electrodinámica Cuántica (QED)

La electrodinámica cuántica, normalmente llamada QED, es una teoría de campo cuántico de la fuerza electromagnética. Tomando el ejemplo de la fuerza entre dos electrones, la teoría clásica del electromagnetismo, la describiría como surgiendo del campo eléctrico producido por cada electrón en la posición del otro. La fuerza se puede calcular por la ley de Coulomb.
El enfoque de la teoría de campo cuántico visualiza la fuerza entre electrones, como una fuerza de intercambio que surge del intercambio defotones virtuales. Se representa por una serie de diagramas de Feynman, siendo el mas básico de tales
Con el tiempo transcurriendo hacia arriba en el diagrama, éste describe la interacción de electrones en la que entran dos electrones, intercambian un fotón, y luego emergen. Utilizando un enfoque matemático conocido como el cálculo de Feynman, se puede calcular la intensidad de la fuerza, con una serie de pasos que asignan contribuciones a cada uno de los tipos de diagramas de Feynman asociados con la fuerza.
La QED se aplica a todos los fenómenos electromagnéticos asociados con las partículas fundamentales cargadas, como los electrones y positrones, y los fenómenos asociados tales como, la producción de pares, la aniquilación electrón-positrón, la dispersión de Compton, etc. Se utilizó para modelar con precisión algunos fenómenos cuánticos que no tenían análogos clásicos tales como, el desplazamiento de Lamb y el momento magnético anómalo del electrón. La QED fue la primera teoría de campos cuántica exitosa, incorporando ideas como la creación y aniquilación de partículas en un marco de trabajo auto-consistente. El desarrollo de la teoría fue la base del Premio Nobel en Física de 1965, otorgado a Richard Feynman, Julian Schwinger y Sin-itero Tomonaga.















Bremsstrahlung (del alemán bremsen "frenar" y Strahlung "radiación","radiación de frenado") es una radiación electromagnética producida por la desaceleración de una partícula cargada, como por ejemplo un electrón, cuando es desviada por otra partícula cargada, como por ejemplo unnúcleo atómico. Este término también se usa para referirse al proceso por el que se produce la radiación. El Bremsstrahlung tiene un espectro continuo. El fenómeno fue descubierto por Nikola Tesla cuando hacía experimentos con altas frecuencias entre 1888 y 1897.
Al Bremsstrahlung también se le conoce como radiación libre-libre ("free-free radiation" en inglés) porque la produce una partícula cargada que está libre antes y después de la deflexión (aceleración) que produce la emisión. Estrictamente hablando, se entiende por Bremsstrahlung cualquier radiación debida a la aceleración de una partícula cargada, como podría ser laradiación de sincrotrón; pero se suele usar sólo para la radiación de electrones que se frenan en la materia.

Bremsstrahlung producido por un electrón de alta energía desviado en el campo eléctrico de un núcleo atómico.

Los rayos X son, básicamente, producidos por electrones de alta energía que bombardean un objetivo, especialmente los objetivos que tienen un alto número de protones (Z). Cuando los electrones que bombardean penetran en el objetivo, algunos electrones viajan cerca del núcleo debido a la atracción de su carga positiva y, posteriormente, se ven influidas por su campo eléctrico. El curso de estos electrones sería desviado, y una parte o la totalidad de su energía cinética se perdería. El principio de la conservación de la energía establece que en la producción de los fotones de rayos X, el electrón ha perdido parte de su energía cinética (KE):
  • KE final del electrón = KE inicial de electrones - energía del fotón de rayos X
La energía "perdida" se emite en forma de fotones de rayos X, específicamente radiación de frenado  de radiación (radiación de frenado es el alemán para 'frenar la radiación'). Bremsstrahlung puede tener cualquier energía que van desde cero hasta el máximo KE de los electrones que bombardean (es decir, 0 a Emax), dependiendo de la cantidad de los electrones se ven influidas por el campo eléctrico, por lo tanto la formación de un espectro continuo. El "pico" del espectro normalmente se produce en aproximadamente un tercio de Emax así que para un espectro de radiación de frenado con un valor Emax de, digamos, 120 keV, el pico del espectro sería de aproximadamente 40 keV.
La intensidad de la radiación bremsstrahlung es proporcional al cuadrado del número atómico del objetivo (Z), el número de cargas unitarias de la partícula bombardeo (z) e inversamente con la masa de la partícula bombardeo (m): Z $ ² $ z / m . De ello se desprende que las partículas de luz, tales como electrones y positrones que bombardean objetivos de alto número atómico son los productores más eficientes de la radiación bremsstrahlung que las partículas más pesadas tales como las partículas alfa o neutrones (que también pueden causar los rayos X que se producen a través de radiación de frenado, aunque es mucho más poco probable que con electrones).
Publicado por en

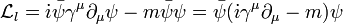
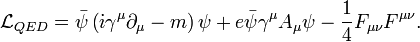
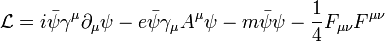
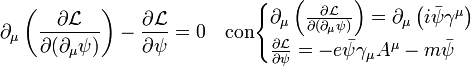
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)