Efectos electromagnéticos
El efecto Hall cuántico (o el efecto Hall cuántico entero) es una versión de la mecánica cuántica del efecto Hall, observado en sistemas bidimensionales con electrones sometidos a bajas temperaturas y fuertes campos magnéticos, en la que la conductividad σ toma los valores cuantizados
donde:
- e es la carga elemental
- h es la constante de Planck. El prefactor
- ν, conocida como el "factor de relleno", puede tener cualquier número entero (ν = 1, 2, 3,...) o valor fraccional (ν = 1/3, 2/5, 3/7, 2/3, 3/5, 1/5, 2/9, 3/13, 5/2, 12/5...).
Pueden distinguirse tanto el efecto Hall cuántico entero como el Efecto Hall cuántico fraccionario, dependiendo de si ν es un entero o una fracción cuántica, respectivamente. El efecto Hall cuántico entero se entiende muy bien y puede explicarse simplemente en términos de orbitales de partículas solas, de un electrón en un campo magnético (véase cuantización de Landau). El efecto Hall cuántico fraccionario es más complicado, ya que su existencia se basa fundamentalmente en las interacciones electrón–electrón. También se entiende muy bien como efecto Hall cuántico entero, no de electrones sino de compuestos de flujo de carga conocidos como fermiones compuestos.
Aplicaciones
La cuantización de la conductancia de Hall tiene la importante propiedad de ser increíblemente precisa. Las medidas reales de la conductancia han resultado ser enteras o múltiplos fraccionarios de e2/h en casi una parte de 1 billón. Este fenómeno, denominado "cuantización exacta", ha demostrado ser una sutil manifestación del principio de invariancia de norma.1 Ha permitido la definición de una nueva práctica estándar para la resistencia eléctrica, basada en la cuantía de la resistencia dada por la constante de von Klitzing RK = h/e2 = 25812.807557(18) Ω.2 Esta es llamada así por Klaus von Klitzing, el descubridor de la cuantización exacta. Desde 1990, un valor fijo convencional RK-90 se utiliza en calibraciones de resistencia en todo el mundo.3 El efecto Hall cuántico proporciona también una determinación independiente y extremadamente precisa de la constante de estructura fina, una cantidad de importancia fundamental en electrodinámica cuántica.
Historia
La cuantización entera de la conductancia de Hall, originalmente fue predicha por Ando, Matsumoto y Uemura en 1975, sobre la base de un cálculo aproximado que ellos mismos no creen que sea verdad. Varios trabajadores posteriormente observaron el efecto en los experimentos llevados a cabo en la capa de inversión de un MOSFET. Sólo en 1980, Klaus von Klitzing, trabajando con muestras desarrolladas por Michael Pepper y Gerhard Dorda, realizó el descubrimiento inesperado de que la conductividad de Hall es exactamente cuantizada. Por este hallazgo von Klitzing fue galardonado con el Premio Nobel de física de 1985. El vínculo entre la cuantización exacta y la invariancia de norma fue encontrado posteriormente por Robert Laughlin. La mayoría de los experimentos sobre el efecto Hall cuántico entero se ejecutan ahora en heteroestructuras de arseniuro de galio, aunque se pueden utilizar muchos otros materiales semiconductores. En 2007, se dio a conocer el efecto Hall cuántico entero en grafeno a temperaturas tan altas como temperatura ambiente,4 y en el óxido ZnO-MgxZnx 1O.5
Efecto Hall cuántico entero– niveles de Landau
En dos dimensiones, cuando electrones clásicos son sometidos a un campo magnético, siguen órbitas circulares de ciclotrón. Cuando el sistema es tratado cuanto-mecánicamente, estas órbitas están cuantizadas. Los niveles de energía de estos orbitales cuantizados toman valores discretos:
donde ωc = eB/m es la frecuencia del ciclotrón.
Estos orbitales son conocidos como niveles de Landau, y en campos magnéticos débiles, su existencia da lugar a muchos interesantes "oscilaciones de cuanto" como las oscilaciones de Shubnikov–de Haas y el efecto de Haas–van Alphen (que a menudo se utiliza para cartografiar la superficie de Fermi de metales).
Para fuertes campos magnéticos, cada nivel de Landau es altamente degenerado (es decir, hay muchos estados de partícula sola que tienen la misma energía En). Específicamente, para una muestra de la zona A, en el campo magnético B, es la degeneración de cada nivel de Landau  (donde gs representa un factor de 2 para la degeneración del giro, y
(donde gs representa un factor de 2 para la degeneración del giro, y  es el cuanto de flujo magnético). Para campos-B suficientemente fuertes, cada nivel de Landau puede tener tantos estados, que todos los electrones libres en el sistema se asientan en sólo unos niveles de Landau; es en este régimen donde se observa el efecto Hall cuántico.
es el cuanto de flujo magnético). Para campos-B suficientemente fuertes, cada nivel de Landau puede tener tantos estados, que todos los electrones libres en el sistema se asientan en sólo unos niveles de Landau; es en este régimen donde se observa el efecto Hall cuántico.
 (donde gs representa un factor de 2 para la degeneración del giro, y
(donde gs representa un factor de 2 para la degeneración del giro, y  es el cuanto de flujo magnético). Para campos-B suficientemente fuertes, cada nivel de Landau puede tener tantos estados, que todos los electrones libres en el sistema se asientan en sólo unos niveles de Landau; es en este régimen donde se observa el efecto Hall cuántico.
es el cuanto de flujo magnético). Para campos-B suficientemente fuertes, cada nivel de Landau puede tener tantos estados, que todos los electrones libres en el sistema se asientan en sólo unos niveles de Landau; es en este régimen donde se observa el efecto Hall cuántico.Matemáticas
Los números enteros que aparecen en el efecto Hall son ejemplos de números cuánticos topológicos. Son conocidos en matemáticas como los primeros números de Chern y están estrechamente relacionados con la fase de Berry. Un modelo llamativo de mucho interés en este contexto es el modelo de Azbel-Harper-Hofstadter cuyo diagrama de fase cuántico es la mariposa de Hofstadter, que se muestra en la figura. El eje vertical es la fuerza del campo magnético y el eje horizontal es elpotencial químico, que fija la densidad de electrones. Los colores representan las conductancias de Hall entero. Colores cálidos representan números enteros positivos y colores fríos enteros negativos. El diagrama de fases es fractal y tiene estructura en todas las escalas. En la figura hay una evidente auto-similaridad.
En cuanto a mecanismos físicos, impurezas o estados concretos (por ejemplo, las corrientes de borde) son importantes para los efectos 'entero' y el 'fraccionario'. Además, la interacción de Coulomb también es esencial en el efecto Hall cuántico. La gran similitud observada entre los efectos de Hall cuántico entero y fraccional, se explica por la tendencia de los electrones a formar estados ligados con un número par de cuantos de flujo magnético, llamados fermiones compuestos .
Efecto Hall es la medición del voltaje transversal en un conductor cuando es puesto en un campo magnético. Mediante esta medición es posible determinar el tipo, concentración y movilidad de portadores en silicio.
Pinza para medir efecto Hall
|
El electromagnetismo enseña que un campo electromagnético variable en el tiempo sólo penetra en un conductor hasta una profundidad del orden del espesor pelicular. El Efecto Hall permite la penetración de un campo magnético rotante y la generación de corriente.
Este método está siendo utilizado para producir corriente necesaria en experimentos de fusión nuclear por confinamiento magnético.
El científico alemán Klaus von Klitzing obtuvo, en 1985, el Premio Nobel de Física por el descubrimiento del efecto Hall cuántico.
Introducción Teórica al efecto Hall
El efecto Hall consiste en que en un metal o semiconductor con corriente, situado en un campo magnético perpendicular al vector densidad de corriente, surge un campo eléctrico transversal y un diferencia de potencial.
fig. 1a fig. 1b
|
La causa del efecto Hall es la desviación que experimentan los electrones que se mueven en el campo magnético bajo la acción de la fuerza de Lorentz.
Las siguientes figuras muestran las direcciones del campo magnético B, de la densidad de corriente J, la fuerza de Lorentz F, la velocidad de las cargas V (según sean estas positivas o negativas), así como los signos de las cargas concentradas en las caras opuestas superior e inferior para cada tipo de carga (negativa y positiva).
La figura 1a) es válida para metales y semiconductores tipo n; para semiconductores tipo p, los signos de las cargas que se concentran en las superficies son opuestos (figura 1b).
Las cargas siguen siendo desviadas por el campo magnético hasta que la acción de la fuerza en el campo eléctrico transversal equilibre la fuerza de Lorentz.
La diferencia de potencial debida al efecto Hall es, pues, en el equilibrio:
jaula de Faraday el efecto por el cual el campo electromagnético en el interior de un conductor en equilibrio es nulo, anulando el efecto de los campos externos. Esto se debe a que, cuando el conductor está sujeto a un campo electromagnético externo, se polariza, de manera que queda cargado positivamente en la dirección en que va el campo electromagnético, y cargado negativamente en el sentido contrario. Puesto que el conductor se ha polarizado, este genera uncampo eléctrico igual en magnitud pero opuesto en sentido al campo electromagnético, luego la suma de ambos campos dentro del conductor será igual a 0.
Se pone de manifiesto en numerosas situaciones cotidianas, por ejemplo, el mal funcionamiento de los teléfonos móviles en el interior de ascensores o edificios con estructura de rejilla de acero. Una manera de comprobarlo es con una radio sintonizada en una emisora de Onda Media. Al rodearla con un periódico, el sonido se escucha correctamente. Sin embargo, si se sustituye el periódico con un papel de aluminio la radio deja de emitir sonidos: el aluminio es un conductor eléctrico y provoca el efecto jaula de Faraday.
Este fenómeno, descubierto por Michael Faraday, tiene una aplicación importante en aviones o en la protección de equipos electrónicos delicados, tales como discos duros o repetidores de radio y televisión situados en cumbres de montañas y expuestos a las perturbaciones electromagnéticas causadas por las tormentas.
Funcionamiento
El funcionamiento de la jaula de Faraday se basa en las propiedades de un conductor en equilibrio electrostático. Cuando la caja metálica se coloca en presencia de un campo eléctrico externo, las cargas positivas se quedan en las posiciones de la red; los electrones, sin embargo, que en un metal son libres, se mueven en sentido contrario al campo eléctrico y, aunque la carga total del conductor es cero, uno de los lados de la caja (en el que se acumulan los electrones) se queda con un exceso de carga negativa, mientras que el otro lado se queda sin electrones (carga positiva).
Demostración teórica
Supongamos el conductor sin equilibrio electrostático. Suponiendo que la carga en el interior del conductor es nula, el potencial V en el interior del conductor cumple la ecuación de Laplace, siendo R la región ocupada por el interior del conductor:
Dado que el conductor está en equilibrio en su superficie no hay corrientes, de modo que el potencial en su superficie es constante:
En virtud del teorema de unicidad del potencial el potencial que cumple tales condiciones es único y puede verse que la solución es trivialmente:
El campo eléctrico en el interior vendrá dado por el gradiente del potencial:
De modo que el campo eléctrico en el interior del conductor es nulo. Es una consecuencia de la ley de Gauss, que dice que en el interior de un conductor hueco, el campo es nulo.
Una jaula de Faraday es una caja metálica que protege de los campos eléctricos estáticos. Debe su nombre al físico Michael Faraday, que construyó una en 1836. Se emplean para proteger de descargas eléctricas, ya que en su interior el campo eléctrico es nulo.
El funcionamiento de la jaula de Farday se basa en las propiedades de un conductor en equilibrio electrostático. Cuando la caja metálica se coloca en presencia de un campo eléctrico externo, las cargas positivas se quedan en las posiciones de la red; los electrones, sin embargo, que en un metal son libres, empiezan a moverse puesto que sobre ellos actúa una fuerza dada por:
Donde e es la carga del electrón. Como la carga del electrón es negativa, los electrones se mueven en sentido contrario al campo eléctrico y, aunque la carga total del conductor es cero, uno de los lados de la caja (en el que se acumulan los electrones) se queda con un exceso de carga negativa, mientras que el otro lado queda con un defecto de electrones (carga positiva). Este desplazamiento de las cargas hace que en el interior de la caja se cree un campo eléctrico (representado en rojo en la siguiente animación) de sentido contrario al campo externo, representado en azul.
El campo eléctrico resultante en el interior del conductor es por tanto nulo
.
Como en el interior de la caja no hay campo, ninguna carga puede atravesarla; por ello se emplea para proteger dispositivos de cargas eléctricas. El fenómeno se denomina apantallamiento eléctrico.
Muchos dispositivos que empleamos en nuestra vida cotidiana están provistos de una jaula de Faraday: los microondas, escáneres, cables, etc. Otros dispositivos, sin estar provistos de una jaula de Faraday actúan como tal: los ascensores, los coches, los aviones, etc. Por esta razón se recomienda permanecer en el interior del coche durante una tormenta eléctrica: su carrocería metálica actúa como una jaula de Faraday.







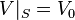


No hay comentarios:
Publicar un comentario