Densidad espectral
Densidad Espectral (Spectral Density) de una señal es una función matemática que nos informa de cómo está distribuida la potencia o la energía (según el caso) de dicha señal sobre las distintas frecuencias de las que está formada, es decir, su espectro.
La definición matemática de la Densidad Espectral (DE) es diferente dependiendo de si se trata de señales definidas en energía, en cuyo caso hablamos de Densidad Espectral de Energía (DEE), o en potencia, en cuyo caso hablamos de Densidad Espectral de Potencia (DEP).
Aunque la densidad espectral no es exactamente lo mismo que el espectro de una señal, a veces ambos términos se usan indistintamente, lo cual, en rigor, es incorrecto.
La definición matemática de la Densidad Espectral (DE) es diferente dependiendo de si se trata de señales definidas en energía, en cuyo caso hablamos de Densidad Espectral de Energía (DEE), o en potencia, en cuyo caso hablamos de Densidad Espectral de Potencia (DEP).
Aunque la densidad espectral no es exactamente lo mismo que el espectro de una señal, a veces ambos términos se usan indistintamente, lo cual, en rigor, es incorrecto.
Definición matemática
Para el caso de señales definidas en energía
Una señal  es definida en energía si su energía media es finita, i.e,
es definida en energía si su energía media es finita, i.e,  y por tanto, su potencia media es cero. Otra forma de decir lo mismo es si la integral de su valor absoluto al cuadrado existe y es finita.
y por tanto, su potencia media es cero. Otra forma de decir lo mismo es si la integral de su valor absoluto al cuadrado existe y es finita.
 es definida en energía si su energía media es finita, i.e,
es definida en energía si su energía media es finita, i.e,  y por tanto, su potencia media es cero. Otra forma de decir lo mismo es si la integral de su valor absoluto al cuadrado existe y es finita.
y por tanto, su potencia media es cero. Otra forma de decir lo mismo es si la integral de su valor absoluto al cuadrado existe y es finita.
Su DEE es
 expresado en [J/Hz]
expresado en [J/Hz]
donde  es la Transformada de Fourier de
es la Transformada de Fourier de  , la integral de esta función en todo el eje
, la integral de esta función en todo el eje  es el valor de la energía total de la señal
es el valor de la energía total de la señal 
 es la Transformada de Fourier de
es la Transformada de Fourier de  , la integral de esta función en todo el eje
, la integral de esta función en todo el eje  es el valor de la energía total de la señal
es el valor de la energía total de la señal 
señales definidas en potencia
Una señal  es definida en potencia si su potencia media es finita, i.e,
es definida en potencia si su potencia media es finita, i.e,  y por tanto, su energía media es infinita,
y por tanto, su energía media es infinita,  .
.
 es definida en potencia si su potencia media es finita, i.e,
es definida en potencia si su potencia media es finita, i.e,  y por tanto, su energía media es infinita,
y por tanto, su energía media es infinita,  .
.
La DEP se calcula usando el teorema de Wiener-Khintchine el cual relaciona la DEP con la transformada de Fourier de la función de autocorrelación
 expresado en [W/Hz]
expresado en [W/Hz]
El valor  es la potencia de la componente continua (DC) de la señal. La integral de esta función en todo el eje
es la potencia de la componente continua (DC) de la señal. La integral de esta función en todo el eje  es el valor de la potencia total de la señal
es el valor de la potencia total de la señal 
 es la potencia de la componente continua (DC) de la señal. La integral de esta función en todo el eje
es la potencia de la componente continua (DC) de la señal. La integral de esta función en todo el eje  es el valor de la potencia total de la señal
es el valor de la potencia total de la señal 
Usando el concepto de correlación cruzada es posible definir también la densidad espectral cruzada.
Nota: En realidad, la definición de la DEP sirve también para las señales definidas en energía, que serían un caso particular. En este caso la Transformada de Fourier de la autocorrelación de la señal x(t) sería simplemente la transformada de Fourier de la señal x(t) al cuadrado, es decir, la DEE.
Propiedades
Relativas a los sistemas lineales e invariantes con el tiempo
En un sistema lineal e invariante con el tiempo en el que  es la entrada,
es la entrada, 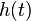 la respuesta al impulso e
la respuesta al impulso e 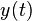 la salida del sistema. Tenemos las siguientes propiedades:
la salida del sistema. Tenemos las siguientes propiedades:
 es la entrada,
es la entrada, 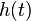 la respuesta al impulso e
la respuesta al impulso e 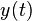 la salida del sistema. Tenemos las siguientes propiedades:
la salida del sistema. Tenemos las siguientes propiedades:
donde  es la media de
es la media de 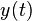 y
y 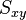 es la densidad espectral cruzada entre
es la densidad espectral cruzada entre  e
e 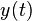
 es la media de
es la media de 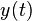 y
y 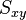 es la densidad espectral cruzada entre
es la densidad espectral cruzada entre  e
e 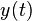
Suma de procesos
En general, la Densidad Espectral de la suma NO es suma de Densidades Espectrales. Esto sólo es cierto si ambos procesos no están correlacionados. En general, si tenemos:
donde  e
e 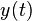 son conjuntamente estacionarios, entonces
son conjuntamente estacionarios, entonces
 e
e 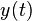 son conjuntamente estacionarios, entonces
son conjuntamente estacionarios, entoncesEstimación de la densidad espectral
Un problema muy común y con grandes aplicaciones prácticas en procesado de señal es el de estimar la densidad espectral de potencia de una señal aleatoria estacionaria. Decimos "estimar" puesto que, como la señal es un proceso estocástico (estacionario) dada la naturaleza estocástica del mismo no es posible determinar con absoluta precisión su DEP a no ser que dispongamos de un registro de señal infinito, lo cual no es posible.
Las técnicas de estimación se dividen en dos grandes grupos:
- No Paramétricas. Están basadas siempre de una u otra forma en el cálculo del periodograma. Calcular la transformada de fourier (en un ordenador es la DFT) de un registro de señal para estimar su espectro es un ejemplo de técnica no paramétrica.
- Paramétricas. Consisten en suponer un determinado modelo para el proceso estocástico (modelos AR, MA, ARMA, etc) y en la estimación de los parámetros de estos modelos mediante técnicas de predicción lineal (filtrado lineal óptimo) u otros métodos.
Acerca de los procesos estocásticos no estacionarios
La DE sólo está matemáticamente bien definida en el caso de señales con una función de autocorrelación estacionaria, i.e, que no dependa de la posición de las variables aleatorias que componen el proceso sino sólo de la distancia entre ellas. Es decir, la DE sólo está bien definida para el caso de señales deterministas y señales aleatorias estacionarias.
Un proceso aleatorio no estacionario que es estacionario a trozos se llama cuasi-estacionario y es posible definir la DEP en cada uno de estos trozos. Para estimar la DEP en este tipo de procesos lo normal es usar un método de estimación espectral paramétrico adaptativo (por ejemplo mediante un modelo AR y el algoritmo LMS para identificar el modelo AR).
Aplicaciones
- Intuitivamente, la Densidad Espectral sirve para identificar periodicidades escondidas en una función de variable continua o de variable discreta (secuencia de números)
- Estimar la entropía de un proceso aleatorio (las señales deterministas obviamente no tienen entropía). Cuanto más plana es la DEP de una señal aleatoria, más entropía contiene. Una señal aleatoria cuya DEP sea perfectamente plana se llama ruido blanco, no contiene redundancia y por tanto no puede ser comprimida (sin pérdidas).
- Una vez conocida su entropía, comprimir con o sin pérdidas una señal de audio o vídeo (codecs FLAC/MP3/OGG, DIVX/THEORA/etc) o restaurar sus propiedades
- Proporciona información muy valiosa sobre la dinámica interna de muchos sistemas físicos. Sirve para identificar elementos o compuestos químicos (espectroscopia). También sirve para la identificación de modelos matemáticos lineales en teoría de control.
Densidad espectral de Potencia
En el ejemplo de la potencia del coseno de frecuencia f0 realizado anteriormente, no nos da información de como esta repartida o esparcida en frecuencia la potencia, solo nos dice su valor. Conociendo la transformada de Fourier nosotros podemos intuir que el grueso de la potencia estará centrado en f0, por ello, nos puede interesar saber como está distribuida la potencia en función de la frecuencia, para ello, se define la densidad espectral de potencia.

Las siglas de DEP en inglés son PSD (Power Spectral Density)
La densidad espectral de potencia difiere de la densidad espectral de energía en que la primera no toma valores infinitos, al estar dividida por T, con lo que podemos representarlo graficamente de forma adecuada. La segunda en cambio, al estar representando la dispersion de la energía en frecuencia y, al ser la energía infinita (con señal periódica), tendrá probablemente zonas de frecuencia que tomen valores infinitos. Como su nombre indican la densidad espectral de potencia nos muestra como esta dispersada la potencia en función de la frecuencia, mientras que la densidad espectral de energía, como esta dispersada la energía.
Probemos ahora, a sacar la DEP de un coseno.

Primeramente, la densidad espectral de energía da infinito (lógico), y la densidad espectral de potencia no podemos resolverla, pues estamos trabajando con valores que tienden a infinito en ciertos puntos, porlo que no nos ha sido de utilidad la función para ver la dispersion de potencia. Para solucionarlo definimos una nueva función.
Difeomorfismo
difeomorfismo es un isomorfismo en la categoría de las variedades diferenciables (es decir, un difeomorfismo es un homeomorfismo diferenciable con inversa diferenciable). Como tal un difeomorfismo es una aplicación que posee aplicación inversa, siendo ambas aplicaciones diferenciables.
Definición
Dadas dos variedades  y
y  , una aplicación diferenciable
, una aplicación diferenciable  es un difeomorfismo si es una aplicación biyectiva y su inversa
es un difeomorfismo si es una aplicación biyectiva y su inversa  también es diferenciable. Si estas funciones son r veces diferenciables con continuidad, entonces f es un Cr-difeomorfismo o difeomorfismo de clase Cr.
también es diferenciable. Si estas funciones son r veces diferenciables con continuidad, entonces f es un Cr-difeomorfismo o difeomorfismo de clase Cr.
 y
y  , una aplicación diferenciable
, una aplicación diferenciable  es un difeomorfismo si es una aplicación biyectiva y su inversa
es un difeomorfismo si es una aplicación biyectiva y su inversa  también es diferenciable. Si estas funciones son r veces diferenciables con continuidad, entonces f es un Cr-difeomorfismo o difeomorfismo de clase Cr.
también es diferenciable. Si estas funciones son r veces diferenciables con continuidad, entonces f es un Cr-difeomorfismo o difeomorfismo de clase Cr.
Dos variedades  y
y  son difeomorfas
son difeomorfas  si existe un difeomorfismo f entre ellas.
si existe un difeomorfismo f entre ellas.
 y
y  son difeomorfas
son difeomorfas  si existe un difeomorfismo f entre ellas.
si existe un difeomorfismo f entre ellas.Difeomorfismos de subconjuntos de variedades
Dado un subconjunto X de una variedad  y un subconjunto
y un subconjunto  , una función
, una función  es diferenciable (suave) si para cada
es diferenciable (suave) si para cada  si existe unentorno
si existe unentorno  de y una función diferencialbe (suave)
de y una función diferencialbe (suave)  tal que
tal que  (nótese que g es una extensión de f). Se dice además que f es un difeomorfismo si es biyectiva, diferenciable y su inversa diferenciable.
(nótese que g es una extensión de f). Se dice además que f es un difeomorfismo si es biyectiva, diferenciable y su inversa diferenciable.
 y un subconjunto
y un subconjunto  , una función
, una función  es diferenciable (suave) si para cada
es diferenciable (suave) si para cada  si existe unentorno
si existe unentorno  de y una función diferencialbe (suave)
de y una función diferencialbe (suave)  tal que
tal que  (nótese que g es una extensión de f). Se dice además que f es un difeomorfismo si es biyectiva, diferenciable y su inversa diferenciable.
(nótese que g es una extensión de f). Se dice además que f es un difeomorfismo si es biyectiva, diferenciable y su inversa diferenciable.Descripción local
Ejemplo canónico. Si U, V son subconjuntos abiertos conexos de  tales que V es además simplemente conexo, una aplicación diferenciable f : U → V es undifeomorfismo, si es una aplicación propia y si la aplicación progrediente o diferencial Dfx : Rn → Rn es biyectiva en todo punto x de U.
tales que V es además simplemente conexo, una aplicación diferenciable f : U → V es undifeomorfismo, si es una aplicación propia y si la aplicación progrediente o diferencial Dfx : Rn → Rn es biyectiva en todo punto x de U.
 tales que V es además simplemente conexo, una aplicación diferenciable f : U → V es undifeomorfismo, si es una aplicación propia y si la aplicación progrediente o diferencial Dfx : Rn → Rn es biyectiva en todo punto x de U.
tales que V es además simplemente conexo, una aplicación diferenciable f : U → V es undifeomorfismo, si es una aplicación propia y si la aplicación progrediente o diferencial Dfx : Rn → Rn es biyectiva en todo punto x de U.Comentario 1. Es esencial que U sea simplemente conexo para que la función f sea globalmente invertible (si únicamente se exige la condición de que la derivada sea biyectiva en cualquier punto). Por ejemplo, considérese la "realificación" de la función compleja z2:
así Dfx es biyectiva en todos los punntos aunque f no admite inversa, porque no es biyectiva, e.g., f(1,0) = (1,0) = f(−1,0).
Ejemplos
Puesto que cualquier variedad puede ser parametrizada localmente mediante  , podemos considerar algunas aplicaciones explícitas:
, podemos considerar algunas aplicaciones explícitas:
 , podemos considerar algunas aplicaciones explícitas:
, podemos considerar algunas aplicaciones explícitas:- Sea
-
- Podemos calcular la matriz jacobiana:
- Esta matriz jacobiana tiene determinante cero si, y sólo si xy = 0. Vemos pues que f es un difeomorfismo sobre cualquier conjunto que no se interseque con los ejes X o Y.
- Sea
-
- donde las
 y
y  son números reales arbitrarios y los términos omitidos son de grado al menos dos en x e y. Calculamos la matriz jacobiana en el punto 0:
son números reales arbitrarios y los términos omitidos son de grado al menos dos en x e y. Calculamos la matriz jacobiana en el punto 0:
- Vemos que g es un isomorfismo local en 0 si, y sólo si
- es decir, los términos lineales en las componentes de g son linealmente independientes, como polinomios.

 significa
significa 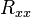 es la función de autocorrelación de
es la función de autocorrelación de 









![S_{zz}(\omega) = S_{xx}(\omega) + S_{yy}(\omega) + 2\mbox{Re}\left[S_{xy}(\omega)\right]](https://upload.wikimedia.org/math/9/f/4/9f4a6463136194352d73021b0539e190.png)







No hay comentarios:
Publicar un comentario