Teoría cuántica de campos axiomática

La teoría cuántica de campos axiomática comprende en realidad varios enfoques formales desarrollados para resolver problemas planteados en el seno de la teoría cuántica de campos convencional.

Introducción

Si bien la mayoría de físicos trabajan dentro de la teoría cuántica de campos convencional a la hora de hacer cálculos prácticos con los que comparar los experimentos y plantear nuevas predicciones, el enfoque de la teoría convencional no es matemáticamente riguroso en varios aspectos y presenta diversos problemas formales. La preocupación teórica por fundamentar de manera matemáticamente consistente la teoría cuántica de campos ha conducido en las últimas décadas a varios intentos teoría cuántica cde campos axiomática. Todos esos intentos incluyen la formulación de ciertos postulados o axiomas, sobre los que construir la teoría. Estos intentos caen en dos clases diferentes:

El primer tipo de enfoques axiomáticos, iniciados durante los años 1950, incluyen los axiomas de Wightman, los de Osterwalder-Schrader y los de Haag-Kastler. Estos intentos trataron de formalizar la noción de "campo con valores en un conjunto de operadores" en el contexto del análisis funcional. Estos intentos tuvieron un éxito limitado, aunque fue posible demostrar que para cualquier teoría de cuántica de campos que satisficiera estos axiomas eran válidos ciertos teoremas generales importantes, como el teorema espín-estadística y el teorema CPT. Sin embargo, no resultó posible probar que las teorías cuánticas de campo realistas disponibles, incluyendo el Modelo estándar satisficieran realmente estos axiomas. De hecho la mayoría de teorías que sabemos satisfacen esos axiomas son físicamente triviales, y en general se restringen a 2 dimensiones o carecen de una dinámica mínimamente interesante. De hecho el área de investigación que trata de crear teorías que satisfagan estos axiomas se denomina teoría cuántica de campos constructiva, un área en la que se lograron ciertos avances en los años 1970 gracias a los trabajos de Segal, Glimm, Jaffe y otros.
El segundo tipo de enfoques axiomáticos, surgió durante los años 1980, y eran teorías axiomáticas basadas en conceptos geométricos. Esta línea de investigación, llamada teoría cuántica de campos topológica, se asocia principalmente con los trabajos de Michael Atiyah y Graeme Segal, y fue ampliada notablemente porEdward Witten, Richard Borcherds y Maxim Kontsevich. Sin embargo, es un hecho conocido que muchos de los modelos físicamente más relevantes de teorías cuánticas de campos, tal como el Modelo estándar, no son teorías cuánticas de campos de tipo topológico. Un ejemplo interesante de teoría cuántica que sí es de tipo topológico es la que da cuenta del efecto Hall cuántico fraccionario. A la postre parece que la teoría cuántica de campos topológica ha tenido mayor impacto en las matemáticas, en particular, en la teoría de representaciones, la topología algebraica y la geometría diferencial.

De hecho encontrar un conjunto apropiado de axiomas para la teoría cuántica de campos, que incluya los ejemplos físicos importantes, es un problema no resuelto de la física matemática. De hecho uno de los problemas del milenio consiste en probar la existencia de una teoría de Yang-Mills de cierto tipo, es un problema asociado al anterior.

Axiomas de Osterwalder-Schrader

Bajo ciertas asunciones técnicas, se ha demostrado que una teoría cuántica de campos euclidiana puede ser Wick-rotada en una QFT de Wightman (ver Axiomas de Osterwalder-Schrader). Este enfoque se basa en el formalismo de las integrales de camino del tipo:

$\int F[\phi(x)]F[\phi(\bar{x})]^* e^{-S[\phi]}\ \mathcal{D}\phi$

Donde:

S[\phi]\,

es el funcional de acción aplicado al campo cuántico.

F[\cdot]

es un polinomio en el campo.

\mathcal{D}\phi

es una medida sobre el conjunto de "trayectorias".

Axiomas de Wightman

Esta es una de las muchas tentativas de poner la teoría cuántica de campos sobre una base matemática firme. Este conjunto de axiomas incorpora supuestos sobre varias cuestiones:

W₀: Asunciones de la mecánica cuántica relativista.
W₁: Asunciones sobre el dominio y la continuidad del campo.
W₂: Ley de transformación del campo.
W₃: Conmutatividad local o causalidad microscópica.

Axiomas de Haag-Kastler

La idea fundamental de este enfoque, llamado también AQFT (Algebraic Quantum Field Theory), es construir una aplicación entre una colección de conjuntos causales del espacio tiempo y una red matemática de C*-álgebras de operadores acotados sobre un espacio de Hilbert. Como conjuntos causales se toman frecuentemente elInterior (topología) de conos dobles. Un cono doble es la intersección del futuro causal de un punto x del espacio-tiempo con el pasado causal de otro punto y(obviamente para obtener un cono doble no trivial es necesario que y esté en el futuro causal de x). La estructura causal de una teoría de campos en este enfoque se basa en que la correspondencia entre la colección de conjuntos abiertos del espacio-tiempo de Minkowski y la red matemática de C*-algebras cumpla ciertas condiciones razonables o axiomas:

Monotonía. Sea 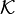$\mathcal{K}$ la colección de conjuntos de code tipo doble cono del espacio-tiempo. Entonces existe una aplicación monotónica $U:\mathcal{K} \to C^*$ tal que: $O_1 \subset O_2 \Rightarrow \exist \alpha_{12}:U(O_1) \to U(O_2)$ tal que $\alpha_{12}\,$ es un homeomorfimos de C*-algebras.
Microcausalidad. Si dos doble conos $O_1 \ne O_2$ están separados espacialmente, es decir, entre cada para de puntos de cada uno de ellos existe una distancia de tipo espacio, entonces $[U(O_1),U(O_2)] = \{0\}$ , es decir, todos los operadores de las respectivas C*-álgebras locales conmutan.
Covariancia frente a traslaciones. Si $U$ es una red de álgebras de operadores definidas sobre un espacio afín, asume que existe una representación fiel y continua $x\mapsto \alpha_x$ del grupo de traslaciones en $Aut U$ (grupo de automorfismos de $U$ ) y $\alpha_x(U(O)) = U(O+x)$ para cualquier doble cono $O$ y cualquier traslación x.
Condición espectral. Sea $G$ el grupo de traslaciones y sea $\omega$ un estado $G$ -invariante de $U$ . Decimos que el par $(U,\omega)$ satisface la condición espectral just cuando existe un subconjunto $G_+$ de $G$ tal que $G_+ \cap (-G_+) = 0$ y en la representación GNS $(H,\pi)$ de $U$ por $\omega$ , el espectro $\mathrm{sp}(U)$ de la representación unitaria inducida está contenida en $G_+$ .
Aditividad sobre el cono de luz
Propiedad del embudo

Teoría de twistores

La teoría de twistores (o tuistores) es una teoría matemática propuesta inicialmente por Roger Penrose en 1967,¹ que mapea los objetos geométricos del espacio-tiempo tetradimensional (espacio de Minkowski) en objetos geométricos del espacio complejo tetradimensional con signatura métrica (2, 2). Las coordenadas en tal espacio se denominan twistores. La teoría de twistores resulta especialmente adecuada para solucionar las ecuaciones del movimiento de los campos sin masa de espínarbitrario.

Un rayo de luz (fotón) como un twistor según la teoría de Roger Penrose

Durante un tiempo se tuvo la esperanza de que la teoría de twistores constituyera por si misma un camino directo hacia la gravedad cuántica, pero esto, en la actualidad, se considera poco probable.

Panorama general

En vez de tratar de explicar cómo las partículas se mueven e interactúan dentro del espacio y del tiempo, la teoría de los twistores propone que el espacio y el tiempo son construcciones secundarias que emergen desde un nivel más profundo de la realidad. En gravedad cuántica se considera habitualmente que la geometría delespacio-tiempo debe fluctuar a escalas cuánticas, alterando cómo los eventos se relacionan entre sí. Debido a estas fluctuaciones cuánticas del espacio-tiempo, un evento que se supone es la causa de otro, puede no serlo, rompiendo la noción de tiempo real y de causalidad, y creando paradojas como las encontradas en las historias de viajes en el tiempo. En la teoría de los twistores, por el contrario, las secuencias causales son primarias, y no fluctúan. En cambio, el lugar y la duración de los eventos si lo hacen.

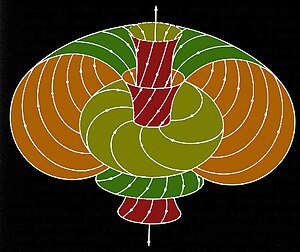
Los twistores son una generalización de una teoría anterior, la de los espinores de Paul Dirac (ver espinor de Dirac), donde se describía el espín de las partículas a la luz de la teoría de la relatividad y la mecánica cuántica. Los twistores son estructuras matemáticas que definen el movimiento y el espín de las partículas y constituyen los "puntos" de un espacio de cuatro dimensiones complejas (ocho dimensiones "reales"). En una analogía, un twistor se puede representar como una familia retorcida de círculos, situada en un sistema de rosquillas encajadas unas dentro de otra. El propio sistema así construido se desplazaría en su totalidad a la velocidad de la luz. En la teoría de los twistores, el concepto de espacio-tiempo se desvanece como consecuencia del principio de incertidumbre, dando regiones difusas. Los twistores individuales representan partículas sin masa, es decir, los bosones. Las partículas con masa o fermiones quedan determinadas por dos o más twistores. Dos de ellos describen los electrones y el resto de leptones. Tres, los protones, neutrones y otros hadrones. Las partículas exóticas como, por ejemplo, algunos quarks, están modelados por más de tres twistores. Las fuerzas se contemplan como deformaciones del espacio twistor. Los bosones distorsionarían el espacio-tiempo porque son portadores ellos mismos de distorsiones, esto es, los propios twistores.

Los twistores tienen una curvatura de tipo helicoidal que describe la quiralidad de las partículas, las vulneraciones de la paridad en interacciones débiles, tal vez la distinción entre carga positiva y carga negativa y, posiblemente también, el sentido único del tiempo. La teoría de twistor surgió con el convencimiento de que la ausencia de antimateria no era exclusivamente una consecuencia de la ruptura de la simetría (ver ruptura espontánea de simetría) como se sugirió en las TGU y en sus ideas sobre las simetrías CPT. La teoría de twistor es asimétrica respecto de la carga, la quiralidad y el tiempo, por lo que parece estar de acuerdo a la aparente vulneración de la simetría CPT en gravedad y cosmología cuántica. De hecho, atendiendo a las ecuaciones de esta teoría, el sentido del tiempo no es algo que haya adquirido el universo después del Big bang. Apareció en la estructura esencial del vacío primigenio.

Detalles

La teoría de twistores es aplicable sólo a un espacio 4D de Minkowski y a la signatura métrica (2,2), y no se generaliza a otras dimensiones o signaturas métricas. En el corazón de la teoría twistor radica el isomorfismo entre el grupo conforme Spin(4,2) y la SU(2,2), que es el grupo de transformaciones unitarias de determinante 1 sobre un espacio vector complejo 4D. Estas transformaciones dejan invariante una norma Hermitiana de signatura (2,2).

$\mathbb{R}^6$ es el espacio vector 6D real correspondiente a la representación vectorial de Spin (4,2).

$\mathbf{R}\mathbb{P}^5$ es la representación proyectiva 5D real correspondiente a la clase de equivalencia de puntos distintos de cero en $\mathbb{R}^6$ bajo la multiplicación escalar.

$\mathbb{M}^c$ se corresponde con el subespacio de $\mathbf{R}\mathbb{P}^5$ correspondiente a los vectores de norma cero. Esto es espacio de Minkowski conformemente compactado.

$\mathbb{T}$ es la representación espinor Weyl complejo 4D y se llama espacio twistor. Tiene una norma invariante hermitiana sesquilineal de signatura (2,2).

$\mathbb{PT}$ es una variedad compleja 3D correspondiente al espacio twistor proyectivo.

$\mathbb{PT}^+$ es el subespacio de $\mathbb{PT}$ correspondiente a twistores proyectivos con norma positiva (el signo de la norma, pero no su valor absoluto es proyectivamente invariante). Este es una variedad compleja 3D.

$\mathbb{PN}$ es el subespacio de $\mathbb{PT}$ que consiste en twistores proyectivos nulos (norma cero). Este es una variedad real-compleja (es decir, tiene 5 dimensiones reales, con cuatro de las dimensiones reales teniendo una estructura compleja haciéndolas dos dimensiones complejas).

$\mathbb{PT}^-$ es el subespacio de $\mathbb{PT}$ de twistores proyectivos con norma negativa.

\mathbb{M}^c

\mathbb{PT}^+

\mathbb{PN}

\mathbb{PT}^-

son todos los espacios homogéneos del grupo conformal.

\mathbb{M}^c

admite una métrica conforme (es decir, una clase de equivalencia de los tensores métricos bajo el reescalado Weyl) con la signatura (+ + + -). Rayos nulos rectos mapean a los rayos nulos consecutivos bajo una transformación conforme y hay un único isomorfismo canónico entre los rayos nulos en

\mathbb{M}^c

y los puntos en

\mathbb{PN}

respetando el grupo conforme.

\mathbb{M}^c

, es el caso en que las soluciones de frecuencia positivas y negativas no pueden ser localmente separadas. Sin embargo, esto es posible en el espacio twistor.

\mathbb{PT}^+ \simeq \mathrm{SU}(2,2)/\left[ \mathrm{SU}(2,1) \times \mathrm{U}(1) \right]

La teoría de cuerdas twistor

Durante muchos años después de la publicación de Penrose en 1967, la teoría de twistor progresaba muy lentamente, en parte debido a problemas matemáticos. La teoría de twistor tampoco parecía relacionado con las ideas de la física contemporánea. Mientras que la teoría de twistor parecía decir algo sobre la gravedad cuántica, sus posibles contribuciones para la comprensión de las otras fuerzas fundamentales y de la física de partículas eran menos evidentes.

La teoría de twistores no logró precisar en qué consiste las fluctuaciones del lugar y la duración de los eventos, hasta que los teóricos de cuerdas mostraron que un evento de localización y tiempo ambiguos era en realidad una cuerda.

La teoría de cuerdas tenía una prometedora explicación para la creación de un espacio, pero no podían hacerla funcionar. Se conjeturó que las partículas moviéndose en cuatro dimensiones pueden comportarse simplemente como cuerdas interaccionando en cinco dimensiones. Lamentablemente este mecanismo sólo producía una dimensión espacial altamente curvada. Usando twistores, se consiguió demostrar cómo todas las dimensiones del espacio ordinario, incluido el tiempo, pueden aparecer.

Edward Witten fue quien propuso la conexión entre la teoría de cuerdas y la geometría twistor, llamando a esta unificación: teoría de cuerdas twistor.² Desarrolló la manera de hacer teoría de cuerdas en un espacio twistor, cuya dimensionalidad era necesariamente la misma que la del espacio-tiempo 3 +1 de Minkowski. La teoría de cuerdas twistor es, por tanto, una posible manera de eliminar la necesidad de más de tres dimensiones espaciales cuando se trabaja con una teoría de (super)cuerdas. Aunque Witten afirmó que creía que la teoría de cuerdas twistor era algo que sólo funcionaba en parte, su trabajo ha dado nueva vida al programa de investigación twistor. Por ejemplo, la teoría de cuerdas twistor puede simplificar el cálculo de la dispersión de amplitudes de los diagramas de Feynman.

Supertwistores

La teoría de cuerdas twistor de Witten se define en el espacio supertwistor. Los supertwistores son un extensión supersimétrica de twistores introducida por Alan Ferber.³ Junto con los grados de libertad twistores estándar, un supertwistor contiene N escalares fermiónicos, donde N es el número de supersimetrías. La álgebra superconforme puede ser realizada en el espacio supertwistor.

AMIGOS PARA SIEMPRE

Páginas

miércoles, 11 de noviembre de 2015

Física matemática