Autocorrelación
La autocorrelación es una herramienta matemática utilizada frecuentemente en el procesado de señales.
La función de autocorrelación se define como la correlación cruzada de la señal consigo misma. La función de autocorrelación resulta de gran utilidad para encontrar patrones repetitivos dentro de una señal, como por ejemplo, la periodicidad de una señal enmascarada bajo el ruido o para identificar la frecuencia fundamental de una señal que no contiene dicha componente, pero aparecen numerosas frecuencias armónicas de esta.
Definiciones de la función de autocorrelación
Dependiendo del campo de estudio se pueden definir diferentes tipos de autocorrelación sin que estas definiciones sean equivalentes. En algunos campos se utilizan indistintamente las funciones de autocorrelación y de autocovarianzas, dado que ambas sólo difieren entre sí en una constante de proporcionalidad que es la varianza (en este caso, la autocovarianza de orden k>0).
Estadística
En estadística, la autocorrelación de una serie temporal discreta de un proceso Xt no es más que simplemente la correlación de dicho proceso con una versión desplazada en el tiempo de la propia serie temporal.
Si Xt representa un proceso estacionario de segundo orden con un valor principal de μ se define entonces:
donde E es el valor esperado y k el desplazamiento temporal considerado (normalmente denominado desfase). Esta función varía dentro del rango [−1, 1], donde 1 indica una correlación perfecta (la señal se superpone perfectamente tras un desplazamiento temporal de k) y −1 indica una anticorrelación perfecta. Es una práctica común en muchas disciplinas el abandonar la normalización por σ3 y utilizar los términos autocorrelación y autocovarianza de manera intercambiable.
Procesado de señal
En el procesado de la señal, dada una señal temporal  , la autocorrelación continua
, la autocorrelación continua  es la correlación continua cruzada de
es la correlación continua cruzada de  consigo mismo tras un desfase
consigo mismo tras un desfase  , y se define como:
, y se define como:
 , la autocorrelación continua
, la autocorrelación continua  es la correlación continua cruzada de
es la correlación continua cruzada de  consigo mismo tras un desfase
consigo mismo tras un desfase  , y se define como:
, y se define como:
donde 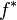 representa el conjugado complejo y el círculo representa una convolución. Para una función real,
representa el conjugado complejo y el círculo representa una convolución. Para una función real,  .
.
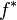 representa el conjugado complejo y el círculo representa una convolución. Para una función real,
representa el conjugado complejo y el círculo representa una convolución. Para una función real,  .
.
Formalmente, la autocorrelación discreta  con un dsfase
con un dsfase  para una señal
para una señal  es
es
 con un dsfase
con un dsfase  para una señal
para una señal  es
es
donde m es el valor esperado de  .
.
 .
.
Frecuentemente las autocorrelaciones se calculan para señales centradas alrededor del cero, es decir con un valor principal de cero. En ese caso la definición de la autocorrelación viene dada por:
Las autocorrelaciones multidimensionales pueden definirse de manera similar. Por ejemplo, en tres dimensiones puede definirse la autocorrelación de una función como:
Propiedades
Definiremos las propiedades de la autocorrelación unidimensional. La mayoría de sus propiedades son extensibles fácilmente a los casos multidimensionales.
- Simetría: R(i) = R(−i),
- La función de autocorrelación alcanza un valor máximo en el origen, donde alcanza un valor real. El mismo resultado puede encontrarse en el caso discreto.
- Como la autocorrelación es un tipo específico de correlación mantiene todas las propiedades de la correlación.
- La autocorrelación de una señal de ruido blanco tendrá un fuerte pico en τ = 0 y valores cercanos a cero y sin ninguna estructura para cualquier otro τ. Esto muestra que el ruido blanco carece de periodicidad.
- Según el teorema de Wiener-Khinchin, la función de autocorrelación es la transformada inversa de Fourier de la densidad espectral:
Igualmente, el espectro se relaciona con la función de autocorrelación:
La consecuencia es que la señal puede expresarse indistintamente en el dominio del tiempo (t) o el dominio de las frecuencias (f), al existir esta correspondencia entre ambos, y entendiendo que la señal está completamente determinada a partir del total de sus momentos o del total de sus frecuencias.
En Mecánica de los Fluidos
Turbulencia
A pesar de que el campo de velocidad instantáneo u(x, t) exhibe un comportamiento aleatorio e impredecible, es afortunadamente posible discernir cantidades estadísticas distintas tales como los valores promedio. Esta importante característica de las fluctuaciones refleja la existencia de escalas características de correlación estadística. Por consiguiente, necesitamos introducir algunas mediciones útiles de las diferentes escalas que describen el estado de los flujos turbulentos. Con este fin, existen 2 medidas comúnmente usadas:
- La función de autocorrelación de la velocidad.
- El espectro energético.
En orden de extraer información estadística del flujo, la velocidad instantánea  se transforma en un valor medio
se transforma en un valor medio  y en un valor fluctuante como se muestra:
y en un valor fluctuante como se muestra:
 se transforma en un valor medio
se transforma en un valor medio  y en un valor fluctuante como se muestra:
y en un valor fluctuante como se muestra:
Donde:  es el componente aleatorio del movimiento y consiste en cualquier instante, de colecciones aleatorias de vórtices. La operación realizada arriba puede ser vista como una separación de escala entre el medio y el campo fluctuante. La función espacio-temporal de correlación se expresa de la siguiente forma:
es el componente aleatorio del movimiento y consiste en cualquier instante, de colecciones aleatorias de vórtices. La operación realizada arriba puede ser vista como una separación de escala entre el medio y el campo fluctuante. La función espacio-temporal de correlación se expresa de la siguiente forma:
 es el componente aleatorio del movimiento y consiste en cualquier instante, de colecciones aleatorias de vórtices. La operación realizada arriba puede ser vista como una separación de escala entre el medio y el campo fluctuante. La función espacio-temporal de correlación se expresa de la siguiente forma:
es el componente aleatorio del movimiento y consiste en cualquier instante, de colecciones aleatorias de vórtices. La operación realizada arriba puede ser vista como una separación de escala entre el medio y el campo fluctuante. La función espacio-temporal de correlación se expresa de la siguiente forma:
En caso de un flujo homogéneo estadísticamente estacionario, las funciones de autocorrelación (tanto en espacio como en tiempo), pueden expresarse como:
Donde:  y
y  y respectivamente
y respectivamente 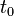 denotan localizaciones (respectivamente un instante dado). La integral espacial y la escala temporal, se definen como:
denotan localizaciones (respectivamente un instante dado). La integral espacial y la escala temporal, se definen como:
 y
y  y respectivamente
y respectivamente 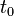 denotan localizaciones (respectivamente un instante dado). La integral espacial y la escala temporal, se definen como:
denotan localizaciones (respectivamente un instante dado). La integral espacial y la escala temporal, se definen como:
La escala integral de la turbulencia “L” provee una medida de la extensión de la región sobre la cual las velocidades están correlacionadas aproximadamente (ej.: el tamaño de los remolinos que llevan la energía del movimiento turbulento). Similarmente “T” provee una medida de la duración temporal sobre la cual las velocidades se mantienen correlacionadas (ej.: la duración de las vueltas de los torbellinos). Por razones obvias, la integral “T” es comúnmente llamada la integral de escala de tiempo de Euler. Así mismo al realizársele la transformada de Fourier a la función de autocorrelación, obtenemos la distribución energética presente en el espectro turbulento.
Aplicaciones
- Una de las aplicaciones de la autocorrelación es la medida de espectros ópticos y en especial la medida de pulsos muy cortos de luz.
- En óptica, la autocorrelación normalizada y la correlación cruzada proporcionan el grado de coherencia de un campo electromagnético.
- En el procesado de señal, la autocorrelación proporciona información sobre las periodicidades de la señal y sus frecuencias características como los armónicos de una nota musical producida por un instrumento determinado (tono y timbre).
¿Qué es la función de autocorrelación (fac)?
La función de autocorrelación (fac) y la función de autocorrelación parcial (facp) miden la relación estadística entre las observaciones de una serie temporal. Por ejemplo, el coeficiente de autocorrelación entre la variable yt y la misma variable un período antes, yt-1, al que denominaremos coeficiente de autocorrelación de primer orden, se formula como:
Dado el supuesto de estacionariedad, se tiene que var(yt) = var(yt-1) , por lo que
En general, para un desfase de k períodos se tiene que:
y cuando k=0,
A efectos de la identificación del modelo, debemos comparar el valor que esta función presentaría para los distintos modelos teóricos, con una estimación de la misma para nuestra serie. Pues bien, el estimador muestral de la fac, para el que utilizaremos la expresión rk, viene dado, con ciertas condiciones y aproximaciones que no trataremos aquí por:

Un campo cuántico libre es un campo cuántico sin autointeracción por lo que su evolución temporal es más sencilla de calcular. Los campos cuánticos libres son aproximaciones al comportamiento de los campos cuánticos con interacción conocidos. Sin embargo, los campos con interacción conducen a fenómenos no lineales complejos y en ocasiones resulta hacer ciertos cálculos con ellos. Los campos cuánticos pueden constituir una primera aproximación a los campos reales bajo ciertas condiciones.
Desde un punto de vista más teórico los campos libres son los únicos modelos consistentes de la teoría cuántica de campos axiomática para campos el espacio-tiempo cuatridimensional que han podido para campos cuánticos tridimensinales.
Introducción
La analogía entre osciladores y campo de la segunda cuantización se aplica directamente en el proceso de cuantización de un campo libre, aquel cuyas ecuaciones de campo son lineales. La equivalencia con un sistema de osciladores armónicos acoplados es exacta, y la energía del campo viene dada por la suma de la energía de cada partícula individual. Puesto que no hay contribuciones adicionales, las partículas son libres y no interaccionan entre sí, de ahí el nombre de campo libre.1 Como consecuencia de la ausencia de interacción, el número de dichas partículas permanece constante.2 Existen sutilezas a tener en cuenta dependiendo del tipo de campo involucrado, o en el caso fermiónico, aunque el proceso y resultados básicos son los mismos.
Detalles matemáticos
Matemáticamente, un campo cuántico libre viene definido por un operador autoadjunto definido para punto del espacio (técnicamente no es una función del espacio tiempo en el conjunto de operadores sino una distribución) este operador tiene ciertos requerimientos de covariancia de Lorentz:
- El campo como un observable que es debe ser autoadjunto:
 .
. - Existe una representación unitaria U del grupo de Poincaré, que representa a las traslaciones espacio-temporales como:

- La misma representación anterior representa a los elementos del grupo de Lorentz como:

- La interacción entre dos observaciones está limitada por relaciones de localidad:
![\eta_{\alpha\beta}(x^\alpha-y^\alpha)(x^\beta-y^\beta) \quad \Rightarrow \quad [\hat{\phi}(x),\hat{\phi}(y)] = 0](https://upload.wikimedia.org/math/2/f/e/2fe57e999bbb80a2f866a068918a322f.png)
Puede demostrarse que en un campo libre que es combinación lineal de operadores de creación y destrucción y satisface los axiomas 1) a 3) anteriores entonces, salvo un factor constante multiplicativo, es de la forma:
La teoría cuántica de campos es el resultado de aplicar el formalismo de la mecánica cuántica a los sistemas de campos continuos, como el campo electromagnético. La descripción matemática de estos sistemas es muy distinta de la de los sistemas discretos, formados por un número finito de partículas interaccionando entre sí, incluso al nivel puramente clásico, como se ha detallado en el capítulo anterior. A nivel cuántico, los estados de una campo cuántico se corresponden con los posibles estados de un colectivo de partículas cuánticas de número indeterminado. En el caso del campo electromagnético, por ejemplo, es conocido que a nivel cuántico este se comporta como un conjunto de partículas llamadas fotones. Esta equivalencia es obvia a la luz de la analogía existente entre un campo continuo y un conjunto deosciladores, como se verá en la sección siguiente.
La teoría cuántica de campos es pues indispensable para describir los fenómenos cuánticos asociados con la radiación electromagnética, por necesitar esta del formalismo de campo continuo. Sin embargo no es esta su única aplicación. Cualquier otro campo «no fundamental», como el campo sonoro, es susceptible de ser tratado mediante esta técnica (véase el ejemplo de más adelante). A nivel microscópico, este no es más que la vibración colectiva de los átomos de un medio, pero aun así la descripción como campo cuántico puede ser útil. Por otro lado, si el campo que se cuantiza es relativista —si sus ecuaciones son invariantes bajo transformaciones de Lorentz—, la dinámica de las partículas que conforman su espectro respetará también dicha invariancia. Además, en un régimen relativista se ha de incluir necesariamente la posibilidad de que el número de partículas del sistema varíe —como en una colisión a altas energías, una desintegración, etc.—. Por ello, para la descripción de las interacciones de un sistema cuántico y relativista es imprescindible utilizar una teoría cuántica de campos.Segunda cuantización
El comportamiento cuántico de un campo es fácilmente comprensible en virtud de la equivalencia entre un campo continuo y un conjunto de osciladores acoplados. Un campo clásico puede entenderse como ellímite continuo de un sistema discreto, cuando la separación media entre las partículas que lo conforman es muy pequeña. Este análisis, que resulta en que el espectro de un campo continuo es equivalente a un conjunto de partículas de número variable, se denomina segunda cuantización.
Modelo simplificado
Un modelo sencillo que ilustra esta equivalencia es un conjunto de osciladores armónicos cuánticos desacoplados, cuyo hamiltoniano es:
Cada oscilador tiene sus propios operadores escalera u operadores de creación y destrucción, ai† y ai, con la definición y propiedades usuales:
los cuales permiten diagonalizar el hamiltoniano total a la forma mostrada. El espectro de energías de este sistema es sencillo. Existe un estado fundamental |0〉, con energíaE0 = Σi ωi/2, aniquilado por cada operador de destrucción, ai |0〉 = 0. Cada operador de creación ai† produce un nuevo nivel con la energía aumentada en ωi. La notación denúmeros de ocupación o de segunda cuantización permite entonces visualizar todo el espectro como:
donde los νi son enteros no negativos, νi = 0 ,1 , ... Llegado este punto, es evidente la analogía que existe entre este sistema, y otro dado por el siguiente hamiltoniano:
donde ni es un operador «número», actuando sobre una serie de estados |ν1, ..., νN〉 de la forma:
Este hamiltoniano describe un sistema con N niveles de energía fijos, con energías ω1, ..., ωN, poblado por un número variable de partículas repartidas por estos. El estado fundamental |0〉 ≡ |0, ..., 0〉 es elvacío, que no contiene partículas en ningún nivel. Estas son indistinguibles ya que los números de ocupación νi no reflejan ninguna diferencia entre las que pueblan el nivel i-ésimo. De hecho son bosones, dado que no hay ninguna restricción sobre el valor de dichos números (pueden ser mayores que 1). Excepto por la constante E0 el espectro de energías de ambos sistemas es idéntico.
Límite continuo en mecánica clásica
Para terminar de entender la equivalencia entre campo y colectivo de partículas, es necesario recordar cómo un campo puede expresarse como el límite continuo de un sistema de osciladores. Para ello, un ejemplo habitual es una varilla elástica capaz de vibrar longitudinalmente. A nivel microscópico, puede imaginarse que se trata de una «cadena» de partículas sobre una recta, espaciadas en equilibrio por una distancia a; y capaces de vibrar dentro de la misma, sujetas a fuerzas elásticas entre ellas. El lagrangiano de este conjunto de partículas es:
(1)
donde cada χn es el desplazamiento de la partícula n-ésima respecto de su posición de equilibrio; m es la masa de estas y K la constante elástica que caracteriza su potencial elástico. Sus ecuaciones de movimiento son entonces:
El comportamiento de este sistema es bien conocido: su movimiento puede descomponerse en una superposición de vibraciones colectivas sencillas, del tipo
(2)
donde k es un «vector de onda» unidimensional, un número en el intervalo 0 < k ≤ 2π/a (por ejemplo, ya que no hay diferencia física entre k y k + 2π/a). La frecuencia depende de k y viene dada por:
(3)
Si se suponen condiciones de contorno periódicas para N de estos «átomos» —que simplifican el análisis y no afectan significativamente al contenido físico— entonces χn =χn + N y k sólo puede ser un múltiplo de 2π/N·a.
Esta descomposición en vibraciones colectivas fundamentales se hace más patente al reexpresar el lagrangiano en función de las coordenadas normales:
(4)
lo que requiere hacer uso de la identidad
donde k recorre los posibles «vectores de onda»: 2π/N a, 4π/N a, ... , 2π/a.
| Osciladores acoplados |  Límite continuo | Campo continuo |
| Dinámica en términos de: | Dinámica en términos de: | |
| Coordenadas normales |  Límite continuo | Ondas planas |
En el límite continuo de este sistema, se toma la distancia de equilibrio entre las partículas muy pequeña, a → 0. Las posiciones de referencia de las partículas, n a, son cada vez más densas dentro de la varilla, y los desplazamientos de cada partícula, χn(t), se transforman en un campo continuo χ(x, t), definido en cada punto de la misma. La coordenada x no describe un grado de libertad, sino que es la versión continua del índice n. Las derivada temporal dχn/dt se corresponde ahora con la derivada parcial ∂tχ(x, t), y la diferencia χn + 1 − χn, cuando a es muy pequeño, es proporcional a la derivada ∂xχ(x, t). En definitiva, al tomar detalladamente el límite en el lagrangiano:
de forma que resulta ser la integral de una densidad lagrangiana. Para que el límite tenga sentido ha de ocurrir simultáneamente que m → 0, K → ∞ y el número de partículas N → ∞, de tal modo que se obtengam/a → μ —la densidad lineal de la varilla— y K a → Y —su módulo elástico—, y que su longitud N a = l sea constante. La ecuación de movimiento de este campo es una ecuación de ondas que describe la propagación del sonido a lo largo de la misma:
Sus soluciones pueden a su vez descomponerse en ondas planas de forma simple:
donde cs2 = Y/μ es la velocidad del sonido. La expresión de estas ondas planas se obtiene en particular a partir de las vibraciones normales ()
en el límite continuo, teniendo en cuenta que cuando k → 0, la frecuencia ()
es proporcional a |k|. El número de ondas k solo puede ser un múltiplo de 2π/l, dado que el campo es periódico, χ(x, t) = χ(x + l, t). Realizando una transformada de Fourier puede expresarse el lagrangiano en términos de estas ondas planas:
donde se han de usar las identidades:
donde ahora k es un múltiplo entero de 2π/l, y δ(x −y) es la delta de Dirac.
Límite continuo en mecánica cuántica
La cuantización del sistema de osciladores acoplados descrito en ()
es una versión más general de la cuantización de un oscilador armónico. El hamiltoniano clásico de los osciladores es:
(5)
donde πn es el momento de la partícula n-ésima. El operador hamiltoniano puede diagonalizarse parcialmente utilizando las coordenadas normales ()
(no se utilizan signos distintos para magnitudes clásicas y sus operadores cuánticos correspondientes):
donde ζk es el momento conjugado de la coordenada normal ηk:
Los operadores escalera tienen una expresión algo más complicada que en el caso de los osciladores desacoplados:
y de este modo, se consigue diagonalizar el hamiltoniano en la forma habitual
El espectro de la teoría es análogo al modelo simplificado anterior, pues esta forma del hamiltoniano es idéntica a un conjunto de osciladores desacoplados, uno por cada modo normal. Suponiendo un estado fundamental |0〉 que es aniquilado por cada ak, ak |0〉 = 0, el resto de niveles de energía se obtienen aplicando operadores de creación o subida ak† sobre este. La energía del estado (ak1†)ν1 (ak2†)ν2 ... |0〉 esωk1 ν1 + ωk2 ν2 + ... + E0, donde la constante E0 = Σk ωk/2 es la energía del nivel fundamental.
Desde la perspectiva de los números de ocupación, puede hablarse de estados poblados por un cierto número de cuantos elementales de la vibración, denominados habitualmente fonones. En el formalismo de segunda cuantización es corriente describir un sistema en términos de estas cuasiparticulas o excitaciones colectivas, que se comportan como partículas individuales. Por «partícula» se entiende «partícula cuańtica», es decir, deslocalizada. Los fonones no tienen una posición determinada, sino que se corresponden con un modo colectivo de vibración, parecido a un estado de momento definido para una partícula libre. Estos fonones tienen un comportamiento bosónico, al igual que en el modelo anterior, ya que puede haber un número arbitrario de ellos en cualquier nivel ωk.
El espectro de energías del campo cuántico es por tanto el límite continuo de este sistema, y el proceso de cuantización puede repetirse paso a paso de manera análoga. El campo χ(x, t) da paso a un operador cuántico χ(x) con momento conjugado π(x). Al tomar el límite continuo del hamiltoniano ()
, se obtiene:
siempre que el momento conjugado continuo se defina mediante el límite πn/a → π(x) cuando a → 0. Esto resulta en que las relaciones de conmutación canónicas en el continuo presentan deltas de Dirac:
Los operadores creación y destrucción se definen entonces como:
Y en términos de estos, el hamiltoniano queda en su forma diagonal:
El espectro de la teoría está formado por estados con un número arbitrario de fonones. La energía cs |k| de estos es arbitrariamente alta. Precisamente por esto la energía del nivel fundamental o vacío |0〉 es formalmente infinita, aunque se considera habitualmente que esta constante no es observable y se ignora.
![R(k) = \frac{E[(X_i - \mu)(X_{i-k} - \mu)]}{\sigma^2}](https://upload.wikimedia.org/math/3/6/e/36eeeb9fd80ab888a70d9831706450fb.png)

















![\begin{align}
&a_i=\sqrt{\frac{m\omega_i}{2}}X_i+i\frac{P_i}{2m\omega_i}\,,\\
&[a_i,a_j]=[a_i^\dagger,a_j^\dagger]=0\text{ , }[a_i,a_j^\dagger]=\delta_{ij}
\end{align}](https://upload.wikimedia.org/math/d/2/1/d218b7a742e390920183e6ff3a2eb0ff.png)

















![a_k=\sqrt{\frac{m\omega_k}2}\eta_k+i\frac{\zeta_{-k}}{\sqrt{2m\omega_k}}=\sqrt{\frac{m\omega_k}{2N}}\sum_n e^{-ikna}\left(\chi_n+i\frac{\pi_n}{m\omega_k}\right)\text{ , }[a_k,a^\dagger_{k'}]=\delta_{kk'}\,,](https://upload.wikimedia.org/math/f/3/4/f34f603983e418ad840a3a03d44e5781.png)


![\frac{i\delta_{nm}}a=[\chi_n,\pi_m/a]\stackrel{a\to0}{\longrightarrow}[\chi(x),\pi(y)]=i\delta(x-y)\!](https://upload.wikimedia.org/math/1/1/b/11b9fe3ea9a6c6802cfae21e0923ae0d.png)


No hay comentarios:
Publicar un comentario