Cálculo integral
Integración de Lebesgue–Stieltjes es una generalización de la integral de Riemann-Stieltjes y la integración de Lebesgue, preservando las muchas ventajas de ambas en un marco más general de teoría de medidas. La integral de Lebesgue-Stieltjes es la integral ordinaria de Lebesgue respecto a una medida conocida como la medida de Lebesgue–Stieltjes, que puede estar asociada a cualquier función de variación finita en la línea real. La medida de Lebesgue-Stieltjes es una medida regular de Borel, y de manera opuesta toda medida regular de Borel en la línea real es de este tipo.
Las integrales de Lebesgue–Stieltjes, nombradas así por Henri Leon Lebesgue y Thomas Joannes Stieltjes, son también conocidas como las integrales de Lebesgue–Radon o simplemente integrales de Radon, debido a Johann Radon, a quien se debe mucha de la teoría. Ellos encontraron aplicaciones en común entre lasprobabilidades y los procesos estocásticos, y en ciertas ramas del análisis matemático incluyendo la teoría del potencial.
Definición
La integral de Lebesgue–Stieltjes:  es definida cuando ƒ : [a,b] → R es Borel-medible y finita y g : [a,b] → R es de variación finita en [a,b] y continua por la derecha, o cuando ƒ es no negativa y g es monótona y continua por la derecha. Para empezar, se asume que ƒ es no negativa y que g es monótona no decreciente y continua por la derecha. Se define w((s,t]) := g(t) − g(s) y w({a}) := 0 (Alternativamente, la construcción funciona para g continua por la izuierda,w([s,t)) := g(t) − g(s) and w({b}) := 0).
es definida cuando ƒ : [a,b] → R es Borel-medible y finita y g : [a,b] → R es de variación finita en [a,b] y continua por la derecha, o cuando ƒ es no negativa y g es monótona y continua por la derecha. Para empezar, se asume que ƒ es no negativa y que g es monótona no decreciente y continua por la derecha. Se define w((s,t]) := g(t) − g(s) y w({a}) := 0 (Alternativamente, la construcción funciona para g continua por la izuierda,w([s,t)) := g(t) − g(s) and w({b}) := 0).
 es definida cuando ƒ : [a,b] → R es Borel-medible y finita y g : [a,b] → R es de variación finita en [a,b] y continua por la derecha, o cuando ƒ es no negativa y g es monótona y continua por la derecha. Para empezar, se asume que ƒ es no negativa y que g es monótona no decreciente y continua por la derecha. Se define w((s,t]) := g(t) − g(s) y w({a}) := 0 (Alternativamente, la construcción funciona para g continua por la izuierda,w([s,t)) := g(t) − g(s) and w({b}) := 0).
es definida cuando ƒ : [a,b] → R es Borel-medible y finita y g : [a,b] → R es de variación finita en [a,b] y continua por la derecha, o cuando ƒ es no negativa y g es monótona y continua por la derecha. Para empezar, se asume que ƒ es no negativa y que g es monótona no decreciente y continua por la derecha. Se define w((s,t]) := g(t) − g(s) y w({a}) := 0 (Alternativamente, la construcción funciona para g continua por la izuierda,w([s,t)) := g(t) − g(s) and w({b}) := 0).
Por el Teorema de Carathéodory, existe una única medida de Borel μg en [a,b] que concuerde con w en cada intervalo I. La medida μg surge de una medida exterior (de hecho, una medida exterior métrica) dada por
el ínfimo entre todas las coberturas de E por los distintos intervalos semiabiertos. Esta medida es llamada comúnmente como1 la medida Lebesgue–Stieltjes asociada ag.
La integral de Lebesgue–Stieltjes
puede ser definida como la integral de Lebesgue de ƒ con respecto a la medida μg en la manera usual. Si g es no decreciente, entonces se define
siendo la última integral definida por la construcción precedente.
Si g es de variación finita y ƒ es finita, entonces es posible plantear
donde g1(x) := Vx
ag es la variación total deg en el intervalo [a,x], y g2(x) = g1(x) − g(x). Tanto g1 como g2 son monótonas no decrecientes. Ahora la integral de Lebesgue–Stieltjes con respecto a g es definida por
ag es la variación total deg en el intervalo [a,x], y g2(x) = g1(x) − g(x). Tanto g1 como g2 son monótonas no decrecientes. Ahora la integral de Lebesgue–Stieltjes con respecto a g es definida por
donde las dos últimas integrales están bien definidas dada la construcción precedente.
Integral de Daniell
Una aproximación alternativa (Hewitt y Stromberg, 1965) es definir la integral de Lebesgue–Stieltjes como la integral de Daniell que extiende la integral usual de Riemann–Stieltjes. Sea g una función no ascendente continua por la derecha en [a,b], y I(ƒ) la integral de Riemann–Stieltjes
para toda función continua ƒ. La operación I define una medida de Radon sobre [a,b]. Esta operación puede ser extendida a la clase de todas las funciones no negativas definiendo
y
Para funciones medibles por Borel, se tiene
y ambos lados de la indentidad definen la integral de Lebesgue–Stieltjes
de h. La medida externa μg es definida a partir de
donde χA es la función característica de A.
Integradores de variación finita son manejados de igual forma a la anterior, descomponiendo en variaciones positivas y negativas.
Ejemplo
Suponga que ![\gamma:[a,b]\to\R^2](https://upload.wikimedia.org/math/0/4/7/0471797b2637de6900b16201888807f4.png) es una curva corregible en el plano y
es una curva corregible en el plano y  es Borel-medible. Entonces se puede definir la longitud de
es Borel-medible. Entonces se puede definir la longitud de  con respecto a la métrica euclidiana medida por
con respecto a la métrica euclidiana medida por  como
como  , donde
, donde  es la longitud de la restricción de
es la longitud de la restricción de  para
para ![[a,t]](https://upload.wikimedia.org/math/4/1/d/41db424f5c02cc7c51f1f480735df0e4.png) . Esta es comúnmente llamada la
. Esta es comúnmente llamada la  -medida de
-medida de  . Esta noción es bastante útil para varias aplicaciones: por ejemplo, en terrenos lodosos la velocidad en que una persona se puede mover depende de la profundidad del lodo. Si
. Esta noción es bastante útil para varias aplicaciones: por ejemplo, en terrenos lodosos la velocidad en que una persona se puede mover depende de la profundidad del lodo. Si  denota la inversa de la velocidad en o cerca de
denota la inversa de la velocidad en o cerca de  , entonces la
, entonces la  -longitud de
-longitud de  es el tiempo que tomaría cruzar
es el tiempo que tomaría cruzar  . El concepto de longitud extrema usa esta noción de
. El concepto de longitud extrema usa esta noción de  -longitud de curvas y es útil en el análisis de transformaciones conformes.
-longitud de curvas y es útil en el análisis de transformaciones conformes.
![\gamma:[a,b]\to\R^2](https://upload.wikimedia.org/math/0/4/7/0471797b2637de6900b16201888807f4.png) es una curva corregible en el plano y
es una curva corregible en el plano y  es Borel-medible. Entonces se puede definir la longitud de
es Borel-medible. Entonces se puede definir la longitud de  con respecto a la métrica euclidiana medida por
con respecto a la métrica euclidiana medida por  como
como  , donde
, donde  es la longitud de la restricción de
es la longitud de la restricción de  para
para ![[a,t]](https://upload.wikimedia.org/math/4/1/d/41db424f5c02cc7c51f1f480735df0e4.png) . Esta es comúnmente llamada la
. Esta es comúnmente llamada la  -medida de
-medida de  . Esta noción es bastante útil para varias aplicaciones: por ejemplo, en terrenos lodosos la velocidad en que una persona se puede mover depende de la profundidad del lodo. Si
. Esta noción es bastante útil para varias aplicaciones: por ejemplo, en terrenos lodosos la velocidad en que una persona se puede mover depende de la profundidad del lodo. Si  denota la inversa de la velocidad en o cerca de
denota la inversa de la velocidad en o cerca de  , entonces la
, entonces la  -longitud de
-longitud de  es el tiempo que tomaría cruzar
es el tiempo que tomaría cruzar  . El concepto de longitud extrema usa esta noción de
. El concepto de longitud extrema usa esta noción de  -longitud de curvas y es útil en el análisis de transformaciones conformes.
-longitud de curvas y es útil en el análisis de transformaciones conformes.Integración por partes
Una función  se considera "regular" en un punto
se considera "regular" en un punto  si existen los límites derecho
si existen los límites derecho  e izquierdo
e izquierdo  , y la función toma el valor promedio, :
, y la función toma el valor promedio, : en el punto límite. Dada las funciones
en el punto límite. Dada las funciones  y
y  de variación finita, si en cada punto
de variación finita, si en cada punto  o
o  es continua, si ambas
es continua, si ambas  y
y  son regulares, estonces existe una fórmula de integración por partes para la integral de Lebesgue–Stieltjes:
son regulares, estonces existe una fórmula de integración por partes para la integral de Lebesgue–Stieltjes:
 se considera "regular" en un punto
se considera "regular" en un punto  si existen los límites derecho
si existen los límites derecho  e izquierdo
e izquierdo  , y la función toma el valor promedio, :
, y la función toma el valor promedio, : en el punto límite. Dada las funciones
en el punto límite. Dada las funciones  y
y  de variación finita, si en cada punto
de variación finita, si en cada punto  o
o  es continua, si ambas
es continua, si ambas  y
y  son regulares, estonces existe una fórmula de integración por partes para la integral de Lebesgue–Stieltjes:
son regulares, estonces existe una fórmula de integración por partes para la integral de Lebesgue–Stieltjes: donde
donde  . Bajo una pequeña generalización de esta fórmula, la condiciones extras en
. Bajo una pequeña generalización de esta fórmula, la condiciones extras en  t
t  pueden ser eliminadas.2
pueden ser eliminadas.2
Un resultado alternativo, de significativa importancia en la teoría del cálculo estocástico es el siguiente: dadas dos funciones
 y
y  de variación finita, donde ambas son continuas por la derecha y tienen límite izquierdo (son funciones 'cadlag') entonces
de variación finita, donde ambas son continuas por la derecha y tienen límite izquierdo (son funciones 'cadlag') entonces
donde . Este resultado puede ser visto como un precursor del Lema de Itō, y es de uso en la teoría general de integración estocástica. El término final es
. Este resultado puede ser visto como un precursor del Lema de Itō, y es de uso en la teoría general de integración estocástica. El término final es ![\Delta U(t)\Delta V(t)= d[U,V]](https://upload.wikimedia.org/math/e/d/d/eddb44e6df556d96038206a4609322fa.png) , que surge de una covarianza cuadrada de
, que surge de una covarianza cuadrada de  y
y  . (El resultado anterior puede ser visto entonces como un resultado relativo a la integral de Stratonovich.)
. (El resultado anterior puede ser visto entonces como un resultado relativo a la integral de Stratonovich.)
 . Este resultado puede ser visto como un precursor del Lema de Itō, y es de uso en la teoría general de integración estocástica. El término final es
. Este resultado puede ser visto como un precursor del Lema de Itō, y es de uso en la teoría general de integración estocástica. El término final es ![\Delta U(t)\Delta V(t)= d[U,V]](https://upload.wikimedia.org/math/e/d/d/eddb44e6df556d96038206a4609322fa.png) , que surge de una covarianza cuadrada de
, que surge de una covarianza cuadrada de  y
y  . (El resultado anterior puede ser visto entonces como un resultado relativo a la integral de Stratonovich.)
. (El resultado anterior puede ser visto entonces como un resultado relativo a la integral de Stratonovich.)Conceptos relacionados
Integración de Lebesgue
Cuando g(x) = x para todo número real x, entonces μg es la medida de Lebesgue, y la integral de Lebesgue–Stieltjes de f con respecto a g es equivalente a la integral de Lebesgue de f.
Integración de Riemann–Stieltjes y teoría de probabilidades
Cuando f es una función continua con valores reales de una variable real, y v es una función real no decreciente, la integral de Lebesgue–Stieltjes es equivalente a laintegral de Riemann-Stieltjes, en cuyo caso usualmente se escribe
para la integral de Lebesgue–Stieltjes, manteniendo implícita la medida μv. Esto es particularmente común en la teoría de la probabilidad cuando v es la distribución de probabilidad de una variable aleatoria continua X, en cuyo caso
![\int_{-\infty}^\infty f(x) \, dv(x) =
\mathrm{E}[f(X)].](https://upload.wikimedia.org/math/7/b/5/7b54cbc29e96d36cd54253a3fd65690e.png)
- algoritmo de Risch, nombrado en honor a Robert H. Risch, es un algoritmo utilizado para el cálculo de integrales indefinidas (es decir, encontrar lafunción primitiva de una función dada).El algoritmo transforma el problema de integración en un problema de álgebra diferencial. Se basa en el tipo de función que se integra y en el uso de métodos para integrar funciones racionales, radicales, logaritmos, y funciones exponenciales.Risch desarrolló el algoritmo en 1968, denominándolo un procedimiento de decisión, porque es un método para decidir si una función posee como integral indefinida una función elemental; y en el caso que la tuviera permite calcularla. En 1976 se desarrolló el algoritmo de Risch-Norman, que aunque es más rápido es una técnica menos poderosa.
Descripción
El algoritmo de Risch se usa para integrar funciones elementales. Laplace resolvió el problema de la integración para el caso de funciones racionales demostrando que la integral de una función racional es otra función racional más un número finito de múltiplos de logaritmos de funciones racionales. El algoritmo sugerido por Laplace se describe en muchos manuales de cálculo elemental pero sólo se implementó algorítmicamente en los años 1960.Liouville formuló el problema cuya solución viene dada por algoritmo de Risch. Liouville consiguió demostrar analíticamente que si existe una función elemental g que sea solución de la ecuación g ′ = f entonces existe un cierto número de constantes αi y funciones elementales ui y v, tales que: Risch desarrolló un método que permite considerar sólo un conjunto finito de funciones elementales de la forma encontrada por Liouville para resolver el problema.La intuición detrás del algoritmo de Risch proviene del comportamiento de las derivadas de las funciones exponencial y logarítmica. Para la función f eg, donde f y gson funciones diferenciables, se tiene:
Risch desarrolló un método que permite considerar sólo un conjunto finito de funciones elementales de la forma encontrada por Liouville para resolver el problema.La intuición detrás del algoritmo de Risch proviene del comportamiento de las derivadas de las funciones exponencial y logarítmica. Para la función f eg, donde f y gson funciones diferenciables, se tiene: por lo que si eg apareciera como resultado de una integración indefinida, entonces debería aparecer dentro de la integral. Igualmente para los logaritmos se tendría:
por lo que si eg apareciera como resultado de una integración indefinida, entonces debería aparecer dentro de la integral. Igualmente para los logaritmos se tendría: entonces si lnng apareciera como resultado de la integración,entonces solo se esperaría que aparecieran unas pequeñas potencias del logaritmo.Una consecuencia importante del algoritmo de Risch es que la integral gaussiana IG no es una función elemental.
entonces si lnng apareciera como resultado de la integración,entonces solo se esperaría que aparecieran unas pequeñas potencias del logaritmo.Una consecuencia importante del algoritmo de Risch es que la integral gaussiana IG no es una función elemental. El algoritmo de Risch, debido a Robert Risch, es un algoritmo para el sistema de álgebra computacional, para el cálculo primitivo, es decir, para determinar una función, sabiendo su derivado. El algoritmo transforma el problema en un problema de álgebra). Se basa en la forma de la función de integrar y métodos para la integración de funciones racionales, radicales, logaritmos y exponencial. Risch, que desarrolló el algoritmo en 1968, fue llamado un procedimiento de decisión, ya que es capaz de determinar si una función tiene una primitiva expresable mediante funciones básicas. El algoritmo de Risch se resume en Algoritmos para Computer Algebra, Keith Geddes, Stephen y George Czapor Labahn. El algoritmo de Risch-Norman, más rápido, pero menos general, fue desarrollado en 1976.
El algoritmo de Risch, debido a Robert Risch, es un algoritmo para el sistema de álgebra computacional, para el cálculo primitivo, es decir, para determinar una función, sabiendo su derivado. El algoritmo transforma el problema en un problema de álgebra). Se basa en la forma de la función de integrar y métodos para la integración de funciones racionales, radicales, logaritmos y exponencial. Risch, que desarrolló el algoritmo en 1968, fue llamado un procedimiento de decisión, ya que es capaz de determinar si una función tiene una primitiva expresable mediante funciones básicas. El algoritmo de Risch se resume en Algoritmos para Computer Algebra, Keith Geddes, Stephen y George Czapor Labahn. El algoritmo de Risch-Norman, más rápido, pero menos general, fue desarrollado en 1976.Descripción
El algoritmo de Risch pretende integrar funciones básicas, es decir, las funciones obtenidas por la composición de funciones exponenciales, logarítmicas, trigonométricas, radicales, y las cuatro operaciones aritméticas. Laplace resuelve este problema para el caso de funciones racionales, mostrando que el original de una función de este tipo es la suma de una logaritmos racionales y múltiples de fracciones racionales. El algoritmo sugerido por Laplace se describe en general en los libros de texto de cálculo; como un programa de ordenador, que se llevó a cabo finalmente en la década de 1960.Entre 1833 y 1841, Liouville rigurosamente formulado el problema resuelto por el algoritmo de Risch. Mostró que si hay una solución básica a la ecuación g g '= f, entonces no son constantes yai y la interfaz de usuario y funciones elementales v tal que la solución es de la forma. Risch desarrolló un método para considerar sólo un conjunto finito de funciones elementales en la forma dada por Liouville.La intuición que conduce a la algoritmo de Risch proviene del comportamiento de la derivada de exponencial y logaritmos. Así, por f e eraasí que si e aparece en una primitiva e ya debería estar en la función original. Del mismo modo, comosi aparece lng, sólo los poderes inferiores del registro deben estar en la función original.Ejemplo
La existencia de una primitiva elemental es extremadamente sensible a los detalles exactos de la función de integrar. Por lo tanto, la siguiente función tiene una primitiva elemental:Pero esto ya no es el caso si 71 se sustituye por 72. La razón de fondo es que el grupo de Galois dees D, es decir, que es generado por las permutaciones y contiene ocho artículos, mientras que el campo de GaloisS es generado por las permutaciones, y contiene 24 elementos.Implementación
La transformación de procedimiento de toma Risch un algoritmo que puede ser ejecutado por un ordenador, y efectivamente, es una tarea compleja que requiere el uso de la heurística y muchas mejoras. De hecho, en 2008, que no sabíamos cualquier software que se ejecuta el algoritmo completo, aunque varios sistemas de álgebra computacional utilizan una aplicación parcial. El axioma es el único anunció que había aplicado plenamente la parte negativa del algoritmo, es decir, si Axiom responde "no" primitivo solicitada no se puede expresar mediante funciones elementales, pero en muchos casos, Axiom se niega a comentar.Por ejemplo, Axiom puede encontrar una primitiva elemental para la función del ejemplo anterior:La solución devuelto es:Muchos otros programas no pueden encontrar una primitiva para esta función solamente con integrales elípticas, funciones especiales que el algoritmo de Risch no sabe cómo tratar.La siguiente función es un ejemplo más complejo, la mayoría del software no se puede integrar mediante la limitación de las funciones básicas:Sin embargo, el original de esta función tiene una forma bastante simple:Decidibilidad
El algoritmo de Risch aplicado a cualquier función básica es en realidad un semi-algoritmo, porque debe verificar que en ciertas etapas de los coeficientes de expresiones parciales obtenidos o no cero. Incluso las expresiones relativamente simples, sabemos que esta pregunta es indecidible: el teorema de Richardson.Tenga en cuenta que este problema también está presente durante muchos algoritmos aparentemente sin problema, como el algoritmo de división polinómica. Por lo tanto, en la práctica, se utiliza la heurística para determinar si estas simplificaciones se cancelan.




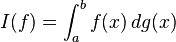
![\overline{I}(h) = \sup \{I(f) | f\in C[a,b], 0\le f\le
h\}](https://upload.wikimedia.org/math/3/2/e/32e3ab9f12a4a1a3a8610c242cd9cc4b.png)
![\overline{\overline{I}}(h) = \inf\{I(f) | f\in C[a,b], h\le
f\}.](https://upload.wikimedia.org/math/3/b/8/3b85c14acdfab6ed5ff2311364c93dac.png)


![U(t)V(t) = U(0)V(0) + \int_{(0,t]}
U(s-)\,dV(s)+\int_{(0,t]} V(s-)\,dU(s)+\sum_{u\in (0,t]} \Delta U_u \Delta V_u,](https://upload.wikimedia.org/math/c/2/b/c2be62cfcd18f0f908062092bd32735b.png)

No hay comentarios:
Publicar un comentario