Cálculo diferencial
derivada de una función en forma paramétrica es una derivada en cálculo que se toma cuando ambas variables x e y (tradicionalmente independiente ydependiente, respectivamente) dependen de una tercera variable independiente t, usualmente tomada como «tiempo».
Primera derivada
Sean  e
e  las coordenadas de los puntos de una curva expresada como una función de variable t. La primera derivada de las ecuaciones paramétricas descritas arriba es dada por:
las coordenadas de los puntos de una curva expresada como una función de variable t. La primera derivada de las ecuaciones paramétricas descritas arriba es dada por:
 e
e  las coordenadas de los puntos de una curva expresada como una función de variable t. La primera derivada de las ecuaciones paramétricas descritas arriba es dada por:
las coordenadas de los puntos de una curva expresada como una función de variable t. La primera derivada de las ecuaciones paramétricas descritas arriba es dada por:
donde la notación  indica la derivada de x con respecto de t, por ejemplo. Para entender el porqué la derivada aparece de esta manera, recuérdese la regla de la cadena para derivadas:
indica la derivada de x con respecto de t, por ejemplo. Para entender el porqué la derivada aparece de esta manera, recuérdese la regla de la cadena para derivadas:
 indica la derivada de x con respecto de t, por ejemplo. Para entender el porqué la derivada aparece de esta manera, recuérdese la regla de la cadena para derivadas:
indica la derivada de x con respecto de t, por ejemplo. Para entender el porqué la derivada aparece de esta manera, recuérdese la regla de la cadena para derivadas:
o en otras palabras
Formalmente, mediante la regla de la cadena:

y dividiendo ambos miembros por  se obtiene la ecuación de arriba.
se obtiene la ecuación de arriba.
 se obtiene la ecuación de arriba.
se obtiene la ecuación de arriba.Segunda derivada
La segunda derivada de una ecuación paramétrica viene dada por
mediante el uso de la regla del cociente para derivadas. El último resultado es muy útil en el cálculo de la curvatura.
Ejemplo
Por ejemplo, considérese el conjunto de funciones donde:
y
Derivando ambas funciones con respecto a t se obtiene que
y
respectivamente. Substituyendo estas en la fórmula para la derivada paramétrica, se obtiene
donde 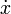 y
y  se entienden como funciones de t.
se entienden como funciones de t.
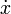 y
y  se entienden como funciones de t.
se entienden como funciones de t.Funciones paramétricasEn algunos casos la ecuación de una función o de una relación no está dada en la formaPor ejemplo, consideremos las ecuaciones Se tiene que a cada valor de La siguiente tabla de valores:  nos permite hacer la representación gráfica de la relación de la siguiente manera:
La relación que determinan las ecuaciones paramétricas, en general no es una función, como sucede en el ejemplo anterior. Sin embargo, en algunos casos, la relación dada sí es una función. Por ejemplo, sean Obtenemos la siguiente tabla de valores:
En algunos casos, en la eliminación del parámetro se utiliza una o más identidades trigonométricas como se muestra a continuación. Sea Se tiene que Vamos a expresar la relación
de donde
Sea ahora R la relación con representación paramétrica En este caso Para expresar R en términos de "x" e "y", se despeja Si Luego la ecuación
Como Luego Su representación gráfica es la siguiente:
El siguiente teorema nos proporciona las condiciones necesarias para obtener la derivada de una función dada en forma paramétrica.
Si Ejemplo: Si  En general, para obtener la enésima derivada, cuando las ecuaciones están dadas en forma paramétrica, se aplica la siguiente igualdad: Derivada en Coordenadas Paramétricas
La derivada es la pendiente de la recta tangente a un punto
lo que significa que:
si parametrizamos la función
entonces si derivamos cada una de las componentes con respecto de
utilizando otra notación que seria definiendo a
Segunda DerivadaEcuación de la Tangente
Para encontrar la ecuación de la normal en coordenadas paramétricas necesitamos tomar en cuenta la ecuación de la recta tangente en coordenadas cartesianas para luego parametrizar.
Tomando otra vez como referencia el punto
entonces si utilizamos la ecuación de la recta
Entonces si parametrizamos con
|



















No hay comentarios:
Publicar un comentario