Ecuaciones
Se denomina ecuación exponencial aquella en la cual la incógnita aparece únicamente en los exponentes de potencias para ciertas bases constantes.1 La incógnita se halla en un exponente de un o unos de los términos. Es decir, un número (u otra variable) está elevada a la incógnita a despejar, normalmente representada por x. Para resolver dichas ecuaciones se recurren a las propiedades de la potenciación, radicación, de logaritmos y cambio de la incógnita por otra.
Formas de resolución
Depende del tipo de ecuación exponencial del que se trate, hay diversas formas de resolverla, por su nivel de complejidad. Las más fáciles son por simple inspección, es decir se descompone la parte numérica en sus factores primos y aplicando logaritmo a ambos lados de la igualdad. A continuación se brindan algunos ejemplos.
Igualación de bases
Sea la ecuación del siguiente ejemplo:
Si el primer miembro sólo tiene un término y el término del segundo miembro es potencia de la base del término del primer miembro, entonces el segundo miembro, se expresa como potencia de la base de la expresión que contiene la incógnita. En el ejemplo 16 es potencia de la base dos de 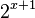 .
.
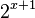 .
.
Luego, por la siguiente propiedad: 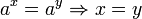 , tenemos:
, tenemos: 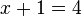
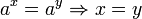 , tenemos:
, tenemos: 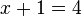
- Un ejemplo algo variado
-
- 42x-1 = 2x
Puesto que 4 = 22 en la ecuación dada resulta
-
- 22(2x-1) = 2x
Finamente, resolviendo 2(2x-1) = x, se obtiene x = 2/3.
Cambio de variables
Sea la ecuación exponencial del ejemplo:
Vamos a escribirla así:
Aplicamos el cambio de variable, y escribimos:
Ahora, al reemplazar, se tiene:
Despejamos  :
:
 :
:
Ahora, recordemos que 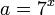 , luego:
, luego:
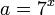 , luego:
, luego:Pasando a una algebraica
Resolver la ecuación2
-
- 2·9x - 3x+1 -2 = 0
Puesto que la ecuación propuesta puede ser escrita en la forma
-
- 2·(3x)2 - 3·3x - 2 = 0
Luego con la sustitución y = 3x, se tiene respecto a y la ecuación algebraica de segundo grado
-
- 2y2 - 3y -2 = 0.
Resolviendo resulta y = 2; y = -1/2. La última solución es imposible, pues 3x > 0. En tal caso 3x = 2;
-
- x = log32 = ln2 : ln3 = 0.6309 ( logaritmos naturales);
Usando logaritmos
Sea la ecuación:
Usamos logaritmo a ambos lados de la ecuación:
Por propiedades de los logaritmos, tenemos:
Operando:
De donde sale:
Otra manera de resolver
Sea la ecuación 4x+1·8x = 4096, pasando las bases de potencia: 4 y 8 a potencias de 2, como también 4096 = 212, se tiene
-
- 22x+2·23x = 212, igualando los exponentes, resulta
- (2x +2) + 3x = 12, finalmente
- 5x = 10; por tanto x = 2.
Ecuaciones exponenciales más complejas
Cuando la incógnita se encuentra en el índice de una raíz, también se la considera exponencial, ya que sólo basta escribirla como exponente fraccionario. Sea la ecuación:
Vemos que la variable se encuentra también en el exponente de una raíz. Por las propiedades de la radicación, vamos a escribirla así:
Aplicamos el método de igualación de bases:
O sea:
Operando, obtenemos:
Otras aplicaciones de las ecuaciones exponenciales
Veamos esta ecuación:
Vemos que se trata de una progresión geométrica. Para resolver esta ecuación no hay más que aplicar la fórmula para calcular la suma de los n términos de unaprogresión geométrica, sabiendo que dicha progresión tiene 5 términos. Así:
Se convierte en:
O sea:
Igualando las bases:
De donde sale:
El mismo razonamiento es aplicable para cualquier progresión geométrica.
El interés compuesto
Si C representa el capital invertido a una tasa de r por ciento anual, y m denota el número de veces al año que se acumula el interés, entonces el monto acumulado Mdespués de x años, se calcula mediante la fórmula:3
-
- M = C(1+r/m)mx
El valor de x se evalúa mediante logaritmos.
También en el caso de la desintegración de cierto material radiactivo, se cumple la fórmula:
-
- Q = Q0·10-kt
donde Q está en gramos; t, en años, Q0 también en gramos y k una constante de variación de la cantidad de sustancia con respecto a la masa de la sustancia.4
Función exponencial
Las ecuaciones exponenciales también surgen cuando se quieren calcular raíces o puntos particulares de las funciones exponenciales. En la función exponencial  , para saber en qué punto su gráfica corta al eje de ordenadas, se debe plantear la ecuación:
, para saber en qué punto su gráfica corta al eje de ordenadas, se debe plantear la ecuación:
 , para saber en qué punto su gráfica corta al eje de ordenadas, se debe plantear la ecuación:
, para saber en qué punto su gráfica corta al eje de ordenadas, se debe plantear la ecuación:
Operando se llega a la conclusión de que 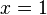 .
.
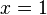 .
.
Si se quiere saber en qué punto del eje de abscisas la gráfica interseca al eje de ordenadas en el punto 1, se plantea:
Otro ejemplo: Hallar el valor de  si tal que
si tal que  si
si 
 si tal que
si tal que  si
si 
Ecuación exponencial |
Una ecuación exponencial es aquella ecuación que incluye alguna potencia en cualquiera de sus términos y en que la incógnita aparece en el exponente.
Para resolver una ecuación exponencial debemos tener en cuenta que:
( a debe ser mayor que cero y distinto de 1)
y que si
(si la base a es igual a la base a, entonces los exponentes serán iguales entre sí)
También debemos recordar las propiedades de las potencias, las que se describen a continuación:
a0 = 1
Toda potencia elevada a cero es igual a 1
a1 = a
Toda potencia elevada a 1 es igual a la base
Toda potencia con exponente negativo es igual al inverso de su base, ahora con exponente positivo en el denominador.
Toda potencia elevada a un exponente fraccionario es igual a una raíz de la base elevada al numerador de la fracción, y el índice de la raíz corresponde al denominador de la fracción.
am • an = am+n
Para multiplicar dos potencias de igual base y distintos exponentes, se conserva la base y esta se eleva a la suma de los exponentes.
am : an = am − n
Para dividir dos potencias de igual base y distintos exponentes, se conserva la base y esta se eleva a la resta de dichos exponentes.
(am)n = am · n
Para elevar una potencia a potencia, se conserva la base y se multiplican los exponentes.
an • bn = (a · b)n
Para multiplicar potencias de distinta base, pero con igual exponente, se multiplican las bases y se conserva el exponente único o común.
an : bn = (a : b)n
Para dividir potencias de distinta base, pero con igual exponente, se dividen las bases y se conserva el exponente único o común.
Nota importante
Debemos tener presente que no existe ninguna fórmula general que indique cómo resolver cualquier ecuación exponencial. Sólo la práctica ayuda a decidir, en cada caso, qué camino tomar.
De todos modos, para resolver una ecuación exponencial hay que realizar algunas acciones previas que son imprescindibles:
Primero:
Si los dos miembros de la igualdad tienen distinta base, debemos reducirlos a la misma base.
Ejemplo:
Segundo:
Una vez que tenemos la misma base en los dos miembros, igualamos los exponentes y resolvemos la ecuación.
Y aquí es donde empiezan las dificultades, ya que si no dominamos las propiedades de las potencias se hará muy difícil resolver este tipo de ecuaciones.
El uso de los logaritmos, como veremos luego en Ecuaciones logarítmicas, facilita en muchas ocasiones la resolución de estas ecuaciones.
Veamos y tratemos de resolver un problema con ecuación exponencial
Sea que tengamos la ecuación exponencial
Vemos que todas las bases son distintas; por lo tanto, trataremos de igualar dichas bases para que nos quede:
Ahora tenemos que el primer término es una potencia elevada a potencia, y deberíamos expresar la ecuación como
Pero, por conveniencia, invertimos los exponentes del primer término, y la expresamos así:
Y vemos que esta ecuación exponencial es una ecuación de segundo grado.
Para resolverla, es necesario el uso de incógnitas auxiliares. Así el problema se simplifica y es fácil comprobarlo.
La incógnita auxiliar para esta ecuación exponencial es:
2(x + 1) = U
Hecho esto, reemplazamos los valores con la incógnita auxiliar, para luego resolver:
U2 + U − 72 = 0
Esta ecuación podría resolverse mediante la fórmula general para resolver ecuaciones de segundo grado, pero como corresponde al caso de factorización de un trinomio perfecto es conveniente por su rapidez utilizar dicha factorización.
Se debe recordar que para hacerla hay que buscar dos números que multiplicados den –72 y que sumados, al mismo tiempo, den 1 (positivo). Estos números son: 9 y –8.
Factorizando queda:
(U + 9) (U − 8) = 0
Luego se igualan ambos paréntesis a cero; se obtienen dos resultados y se elige el que sea correcto.
U + 9 = 0 U − 8 = 0
U = −9 U = 8
De los dos resultados, el correcto es U = 8, porque 23 = 8.
En cambio − 9 no se puede llevar a una base 2
(Recordemos que para resolver cualquier ecuación exponencial siempre deben igualarse las bases; en este ejercicio todas las bases deben ser 2).
Entonces, sabiendo que
U = 8; podemos reemplazar el valor de la incógnita y resolver:
2(x+1) = 8
2(x+1) = 23
Por lo tanto:
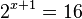
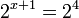
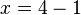
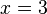

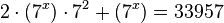
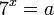
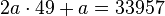


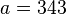
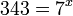

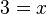
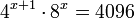
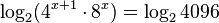

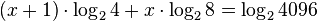
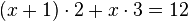
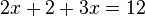

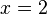
![\sqrt[3x + 1]{2^{x + 2}} = 8](https://upload.wikimedia.org/math/f/0/3/f03efeca7d6991838b1e272c3f1ff959.png)
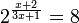







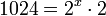


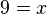

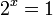
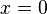



No hay comentarios:
Publicar un comentario