Ecuaciones
ecuación funcional es una ecuación que se expresa a través de una combinación de variables independientes y funcionesincógnitas, cuya expresión y valor deben ser resueltos. Es posible determinar las propiedades de las funciones analizando los tipos de ecuaciones funcionales que las mismas satisfacen. El término ecuación funcional está por lo general reservado a ecuaciones que no son fácilmente reducibles a ecuaciones algebraicas: esto se debe a que en muchos casos dos o más funciones conocidas son substituidas como argumentos de una función incógnita, que debe ser resuelta.
Ecuación funcional elemental
Se llama ecuación funcional elemental a aquella que conlleva como incógnita una función de una variable. Los elementos que contienen la función están ligados por suma (diferencia), producto (cociente), producto por un escalar o la composición de funciones.1
- Ejemplo: |f(x) + 1| = 3x + 3
- Ejemplo: Halle las f(X) tales que [f(x)]^2f(1-x/1+x) = 64x para todo x real distinto a 1, 0,-1.2
- Sea la ecuación funcional fºf(x)= 4x+ 3, donde º es composición de funciones, hallar f(x)'.
Similarmente, en el caso de las ecuaciones diferenciales ordinarias, una función (o aplicación) aparece como una incógnita. Por ejemplo, y' = ky, cuya solución es una familia de funciones monoparamétrica.
Ejemplos
- La ecuación funcional
- es satisfecha por la función zeta de Riemann ζ. El símbolo Γ identifica a la función gamma.
- La ecuación funcional
- es satisfecha por la función gamma.
- La fórmula de reflexión de Euler:
- es satisfecha por la función gamma.
- La ecuación funcional
- donde a, b, c, d son enteros tales que ad − bc = 1, define f que es una forma modular de orden k.
- Ejemplos de algunas funciones menos conocidas:
-
- f(x + y) = f(x)f(y), satisfecha por todas las funciones exponenciales.
-
- f(xy) = f(x) + f(y), satisfecha por todas las funciones logarítmicas.
-
- f(x + y) = f(x) + f(y) (ecuación funcional de Cauchy).
-
- f(x + y) + f(x − y) = 2f(x) + 2f(y) (ecuación cuadrática o ley del paralelogramo).
-
- F(az) = aF(z)(1 − F(z)) (ecuación de Poincaré).
-
- G(z) = λ−1 G(G(λz)) (teoría del caos, scaling).
-
- f((x + y)/2) = (f(x) + f(y))/2 (Jensen).
-
- g(x + y) + g(x − y) = 2g(x)g(y) (d'Alembert).
-
- f(h(x)) = cf(x) (ecuación de Schröder).
-
- f(h(x)) = f(x) + 1 (ecuación de Abel).
- Un tipo simple de ecuación funcional es una relación de recurrencia. Formalmente hablando, esto involucra una función de variable entera, y también aoperadores de traslación.
- Un ejemplo de una relación de recurrencia es
- Las leyes conmutativa y asociativa son ecuaciones funcionales. Cuando la ley asociativa se expresa en su forma usual, se coloca un símbolo entre dos variables para representar una operación binaria, o sea:
-
- (a * b) * c = a * (b * c),
- Pero si se escribe f(a, b) en vez de a * b, entonces la ley asociativa se parece más a lo que convencionalmente se considera como una ecuación funcional:
-
- f(f(a, b), c) = f(a, f(b, c)).
Un aspecto en común que comparten todos los ejemplos indicados previamente es que en cada uno de los casos dos o más funciones conocidas (algunas veces la multiplicación por una constante, otras la suma de dos variables, o aún la función identidad) son substituidas en la función incógnita que se desea resolver.
Si se pretenden obtener todas las soluciones, es posible que deban emplearse condiciones propias del análisis matemático; por ejemplo, en el caso de la ecuación de Cauchy mencionada previamente, las soluciones que son funciones continuas son las 'razonables', mientras que las otras soluciones que no es probable que tengan aplicaciones prácticas se pueden construir (utilizando una base de Hamel para los números reales como espacio vectorial sobre los números racionales). El teorema de Bohr-Mollerup es otro ejemplo muy conocido.
Resolución de ecuaciones funcionales
La resolución de ecuaciones funcionales puede ser muy difícil, en esta sección se discuten algunos métodos que se suelen utilizar para resolverlas. Es importante analizar las funciones involutivas para poder resolver ecuaciones funcionales. Por ejemplo, si se considera la función 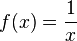 . Luego consideremos f(f(x)) = x, si se continua con este patrón se concluye que se obtiene x para un número par de composiciones y f(x) para un número impar. Esta misma idea se aplica a muchas otras funciones, como ser
. Luego consideremos f(f(x)) = x, si se continua con este patrón se concluye que se obtiene x para un número par de composiciones y f(x) para un número impar. Esta misma idea se aplica a muchas otras funciones, como ser  entre otras.
entre otras.
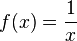 . Luego consideremos f(f(x)) = x, si se continua con este patrón se concluye que se obtiene x para un número par de composiciones y f(x) para un número impar. Esta misma idea se aplica a muchas otras funciones, como ser
. Luego consideremos f(f(x)) = x, si se continua con este patrón se concluye que se obtiene x para un número par de composiciones y f(x) para un número impar. Esta misma idea se aplica a muchas otras funciones, como ser  entre otras.
entre otras.
Ejemplo 1: Resolver 

Sea 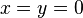 :
: 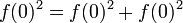 . Por lo tanto
. Por lo tanto  y
y 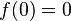 .
.
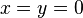 :
: 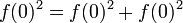 . Por lo tanto
. Por lo tanto  y
y 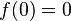 .
.
Si, se hace  :
:
 :
:
Un cuadrado de un número real es no negativo, y la suma de números no negativos es cero solo si ambos números son 0. Por lo tanto  para todo x y
para todo x y  es la única solución.
es la única solución.
 para todo x y
para todo x y  es la única solución.
es la única solución.
Ecuaciones Funcionales.
Las ecuaciones funcionales son ecuaciones en las que tenemos una relación entre una función en un punto ó en varios, y sus derivadas ó sucesivas evaluaciones.
Pondremos varios ejemplos para que se puedan ver distintas formas de abordar un problema de este tipo:
Para empezar, como tenemos x e y podemos probar a hacer algunas sustituciones con números.
Lo primero de todo, llamemos  . Entonces es fácil ver que con
. Entonces es fácil ver que con  , obtenemos:
, obtenemos:
Ahora que sabemos los valores de  , podemos probar con
, podemos probar con  :
:
Parece evidente que si  , se cumplirá que
, se cumplirá que  para todo
para todo  , así que intentemos probarlo por inducción.
, así que intentemos probarlo por inducción.
Así que todas las funciones posibles son 
Observación
Las funciones  que cumplen que
que cumplen que  son también
son también  , ya que, sea
, ya que, sea  con
con  , se cumple que
, se cumple que
Hallar todas las funciones  tales que
tales que
Sustituyendo x por y obtenemos que:
Encontrar todas las funciones  tales que
tales que 
(OME-fase nacional 2001)
Supongamos que existe una función  tal que
tal que  .
.
Entonces, si , se cumple que
, se cumple que
Por lo que tenemos que  , y además
, y además 
Pero entonces, haciendo  en la primera igualdad y
en la primera igualdad y  en la segunda, tenemos que
en la segunda, tenemos que  , por lo que
, por lo que  , contradicción con que
, contradicción con que  .
.
La ecuación funcional de Cauchy es una ecuación funcional considerada entre las más simples de representar; sin embargo, su solución sobre los números reales es extremadamente complicada. La ecuación es
Sobre los números racionales, puede demostrarse usando álgebra elemental que hay una única familia de soluciones  para cualquier constante c arbitraria.
para cualquier constante c arbitraria.
 para cualquier constante c arbitraria.
para cualquier constante c arbitraria.
Esta familia de soluciones aplica también sobre los reales, pero algunas restricciones adicionales sobre la función f, como las siguientes, pueden resultar en otras soluciones:
- si f es una función continua (probada por Cauchy en 1821). Esta condición fue debilitada en 1875 por Jean Gaston Darboux quien demostró que sólo es necesario que la función sea continua en un punto.
- si f es una función monótona sobre cualquier intervalo.
- si f es una función acotada en cualquier intervalo.
Por otro lado, si no hay condiciones adicionales sobre f, luego (asumiendo el axioma de elección) hay otras infinitas funciones posibles que satisfacen la ecuación. Esto fue demostrado en 1905 por Georg Hamel utilizando las bases de Hamel. El quinto problema de Hilbertes una generalización de esta ecuación.
Soluci´on del Problema de ecuaciones funcionales. - .................................................:http://www.um.es/prinum/problemasmates/problemas/solucion_problema_ecua_funciones.pdf


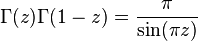


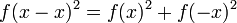


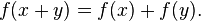
No hay comentarios:
Publicar un comentario