Ecuaciones
la Ecuación de Fisher (Fisher's equation en inglés), fue nombrado por el Británico estadístico y biólogoRonald Fisher, también conocido como la Ecuación de Kolmogorov-Petrovsky-Piscounov) es la ecuación en derivadas parciales.
Fisher propuso esta ecuación en el contexto de la biología evolutiva y dinámica de poblaciones por describir la extensión en el espacio del alelo ventajoso y explorando sus soluciones de olas que viajan.1 Por cada ola velocidad  (
(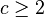 en forma sin dimensión admite una solución de onda viajando de esta forma
en forma sin dimensión admite una solución de onda viajando de esta forma
 (
(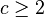 en forma sin dimensión admite una solución de onda viajando de esta forma
en forma sin dimensión admite una solución de onda viajando de esta forma
donde  está incrementando y
está incrementando y
 está incrementando y
está incrementando y
O sea, la solución cambie de un estado de equilibrio u = 0 a un estado de equilibrio u = 1. No existe tal solución por c < 2.1 2 3 La forma de la ola por una velocidad de ola ya dada es único. Las soluciones por las olas que viajan están estables en contra de perturbaciones en el campo cerca pero no a perturbaciones del campo lejos, las cuales pueden hacer más gruesa la cola. Usando el principio de comparación y la teoría que todas las soluciones con datosinciales compactos convergen a olas con la velocidad mínima.
Por la velocidad de olas especializada 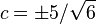 , todas las soluciones se puedan encontrar en una forma cerrada,4 con
, todas las soluciones se puedan encontrar en una forma cerrada,4 con
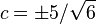 , todas las soluciones se puedan encontrar en una forma cerrada,4 con
, todas las soluciones se puedan encontrar en una forma cerrada,4 con
donde  es arbitrario y las condiciones del límite por arriba están satisfactorias por
es arbitrario y las condiciones del límite por arriba están satisfactorias por 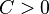 .
.
 es arbitrario y las condiciones del límite por arriba están satisfactorias por
es arbitrario y las condiciones del límite por arriba están satisfactorias por 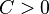 .
.
Es quizás el ejemplo más sencillo de un sistema de reacción-difusión semilinear
lo cual puede exhibir soluciones de olas que viajan dado porque cambian entre estados de equilibrio dado por  . Tales ecuaciones ocurren por ejemplo en laecología, la fisiología, la combustión, cristalización, plasma, y problemas generales de cambio de estado.
. Tales ecuaciones ocurren por ejemplo en laecología, la fisiología, la combustión, cristalización, plasma, y problemas generales de cambio de estado.
 . Tales ecuaciones ocurren por ejemplo en laecología, la fisiología, la combustión, cristalización, plasma, y problemas generales de cambio de estado.
. Tales ecuaciones ocurren por ejemplo en laecología, la fisiología, la combustión, cristalización, plasma, y problemas generales de cambio de estado.
Prueba de la existencia de soluciones de olas viajando y el análisis de sus propiedades se hace muchas veces usando el método de fases de espacio.
Si X va al banco y este le ofrece un 4% de interés anual, se refiere al valor nominal. Porque si tuvieramos en cuenta que la inflación ese año es, por ejemplo, del 1,5%, el valor real sería
4 - 1,5 = 2,5%
La ecuación de Fisher por tanto sería:
i = r + pi
siendo "i" el interés, "r" el valor real y "pi" la inflación.
4 - 1,5 = 2,5%
La ecuación de Fisher por tanto sería:
i = r + pi
siendo "i" el interés, "r" el valor real y "pi" la inflación.
Ecuación de Fisher .- ....................................................:http://www.palermo.edu/economicas/cbrs/pdf/rwe9/PBR9_03WEB.pdf
ecuación de Harris-Benedict es una ecuación empírica para estimar el metabolismo basal de una persona en función de su peso corporal, estatura y edad, y es utilizado en conjunto con factores de actividad física, para calcular la recomendación de consumo diario de calorías para un individuo. La ecuación supone una composición corporal normal, con una relación media entre la masa muscular y la masa grasa, por lo que puede ser inexacta para las personas que son muy musculosas (la fórmula subestima las necesidades reales) o para las personas con sobrepeso (la ecuación sobreestima las necesidades reales).
Cálculo de la tasa metabólica basal
Las ecuaciones originales de Harris-Benedict publicados en 1918 y 1919:1
| Hombres | TMB = 66,4730 + (13,7516 x peso en kg) + (5,0033 x altura en cm) - (6,7550 x edad en años) |
| Mujeres | TMB = 655,0955 + (9,5634 x peso en kg) + (1,8449 x altura en cm) - (4,6756 x edad en años) |
Las ecuaciones de Harris-Benedict revisadas por Roza y Shizgal en 1984:2
| Hombres | TMB = 88,362 + (13,397 x peso en kg) + (4,799 x altura en cm) - (5,677 x edad en años) |
| Mujeres | TMB = 447,593 + (9,247 x peso en kg) + (3,098 x altura en cm) - (4,330 x edad en años) |
Las ecuaciones de Harris-Benedict revisadas por Mifflin y St Jeor en 1990 y utilizadas en la actualidad:3
| Hombres | TMB = (10 x peso en kg) + (6,25 × altura en cm) - (5 × edad en años) + 5 |
| Mujeres | TMB = (10 x peso en kg) + (6,25 × altura en cm) - (5 × edad en años) - 161 |
Ingesta diaria de calorías recomendada según el principio de Harris-Benedict
La siguiente tabla permite el cálculo de la ingesta diaria de calorías recomendada de una persona para mantener su peso actual:4
| Poco o ningún ejercicio | Calorías diarias necesarias = TMB x 1,2 |
| Ejercicio ligero (1-3 días a la semana) | Calorías diarias necesarias = TMB x 1,375 |
| Ejercicio moderado (3-5 días a la semana) | Calorías diarias necesarias = TMB x 1,55 |
| Ejercicio fuerte (6-7 días a la semana) | Calorías diarias necesarias = TMB x 1,725 |
| Ejercicio muy fuerte (dos veces al día, entrenamientos muy duros) | Calorías diarias necesarias = TMB x 1,9 |
Historia de la fórmula de Harris-Benedict
En 1919, el Laboratorio de Nutrición del Instituto Carnegie de Washington (EE.UU.), publica una monografía con el título “A Biometric Study of Basal Metabolism in Man”. Los autores de esta publicación fueron los fisiólogos-nutricionistas J. Arthur Harris y Francis G. Benedict.
En esta monografía Harris y Benedict evaluaron parámetros metabólicos de 136 hombres y 106 mujeres, todos adultos sanos. A estos sujetos se les realizó calorimetría indirecta y a partir de la evaluación de sus datos con análisis de regresión, se diseñaron fórmulas matemáticas para predecir el gasto energético en reposo, usando como variables la edad, el género, el peso y talla.
En 1984, los datos y la fórmula original de Harris y Benedict fueron re-evaluados por Roza y Shizga determinando la masa celular activa total con mediciones de potasio corporal total (Ke). Basándose en sus resultados, propusieron algunas variantes a esa fórmula original de 1919.
En 1990, Pellet publica en el American Journal of Clinical Nutrition una completa revisión sobre las fórmulas matemáticas utilizadas para predecir el gasto energético en reposo. En esta publicación aparece una actualización de la fórmula original de Harris y Benedict que es la que se utiliza hoy en día.
Usos para perder peso
Si utilizamos la última fórmula descrita en las tablas, un hombre de 24 años, 80 kg y 180 cm, resulta tener una tasa metabólica basal (TMB) de 1.810. Si además practica ejercicio moderadamente, habría que multiplicar la TMB por su nivel de actividad (1.810 x 1,55). Obtenemos así 2.805 kcal por día para mantener su peso actual de 80 kg. Aunque esto parezca una ingesta alta de calorías, es lo que su nivel de actividad precisa. Este individuo no perdería peso si mantiene su nivel de actividad y su ingesta. La misma persona solo podría consumir 2.172 kcal al día sin ganar peso en el caso de que no realizara ningún tipo de ejercicio.
Utilizando la ecuación de Harris-Benedict, se puede adecuar la toma de calorías para perder peso. Un kilogramo de grasa corporal contiene aproximadamente 7.000 kcal.5 Según la ecuación de Harris-Benedict, si alguien con una TMB de 2.500 kcal consume solo 2.000, debería perder 1 kg en 14 días.
ECUACIONES HARRIS-BENEDICT
Las ecuaciones Harris-Benedict son las siguientes:
TMB Mujer = 655 + (9,6 * P) + (1,8 * A) – (4,7 * E)
TMB Hombre = 66 + (13,7 * P) + (5 * A) – (6,8 * E)
ECUACIONES DE HARRIS-BENEDICT – NOMENCLATURA
P: Peso en Kilogramos
A: Altura en centímetros
E: Edad en años
Una vez obtenida la TMB, se multiplica el Factor de Actividad:
Sedentario: CCD = TMB * 1,2 (trabajo de escritorio – sin ejercicio)
Actividad Ligera: CCD = TMB * 1,375 (ejercicio 1-3 días por semana)
Actividad Moderada: CCD = TMB * 1,55 (ejercicio 3-5 días por semana)
Actividad Intensa: CCD = TMB * 1,725 (ejercicio 6-7 días por semana)
Actividad Muy Intensa: CCD = TMB * 1,9 (ejercicio 2 veces al día, ejercicios de mucha fuerza y agotamiento, deportistas profesionales)
ECUACIONES DE HARRIS-BENEDICT – EJEMPLO PRÁCTICO
Una mujer, de 25 Años de edad, que mide 1,62 Metros y pesa 69 Kilogramos, la ecuación, queda de la siguiente manera:
P: 69Kg
A: 162 cm
E: 25 años
TMB Mujer = 655 + (9,6 * 69) + (1,8 * 162) – (4,7 * 25)
TMB Mujer = 1492 Kcal
Una vez obtenida la tasa de metabolismo basal (TMB) el resultado se multiplica por el Factor de Actividad. Vamos a suponer que la mujer del ejemplo, tiene un trabajo de oficina y 3 veces a la semana va al gimnasio. Su factor de actividad, sería de 1,375:
CCD = 1492 * 1,375
CCD = 2052 Kcal
El resultado final, es que esta mujer, necesita al día consumir 2052 Kcal. Es la base para iniciar una dieta, dependiendo de los objetivos que se persigan (adelgazar, aumentar de peso, o mantenerse).





No hay comentarios:
Publicar un comentario