Ecuaciones integrales
ecuación integral es una ecuación en que la función incógnita aparece dentro de una integral. Existe una conexión estrecha entre las ecuaciones integrales y las ecuaciones diferenciales, y de hecho algunos problemas pueden formularse como ecuación diferencial o equivalentemente como ecuación integral. Ver por ejemplo el modelo de Maxwell de viscoelasticidad.
Introducción
El tipo de ecuación integral más sencillo es el de una ecuación de Fredholm de primera clase:1
Donde:
- φ es una función desconocida,
- f es una función conocida y
- K es una función de dos variables también conocida, llamada núcleo de la integral.
Nótese que los límites de integración son constantes, esto precisamente es lo que caracteriza a una ecuación de Fredholm. Si la función incógnita aparece también fuera de la integral, entonces se tiene una ecuación de Fredholm de segunda clase:
El parámetro lambda es un número real desconocido que desempeña el mismo papel que de un valor propio en una expresión de álgebra lineal.
Si un límite de integración es variable, entonces se tiene una ecuación de Volterra, las ecuaciones de Volterra de primer y segundo tipo vienen dadas por:
En todo lo anterior, si la función f es idénticamente nula, la ecuación integral se llama ecuación integral homogénea. Si f no es cero, entonces se trata de una ecuación integral inhomogénea.
Clasificación
Las ecuaciones integrales se clasifican según tres criterios dicotómicos que combinados dan ocho tipos de ecuaciones diferentes:
- Límites de integración:
- Ambos fijos: Ecuación integral de Fredholm
- Uno de ellos variable: Ecuación integral de Volterra
- Lugar donde aparece la función incógita:
- Únicamente dentro de la integral: ecuación integral de primera clase
- Tanto dentro de la integral como fuera: ecuación integral de segunda clase
- Homogeneidad, según f sea o no nula:
- Si f es idénticamente nula: ecuación integral homogénea.
- Si f no es nula: ecuación integral inhomogénea.
Las ecuaciones integrales son importantes en muchas aplicaciones. Los problemas en los que aparecen ecuaciones integrales incluyen los problemas de transferencia de energía por radiación, el problema de vibraciones de una cuerda o una membrana, los problemas de viscoelasticidad y algunos problemas de campos electromagnéticos. Algunos de estos otros problemas también pueden plantearse en términos de ecuaciones diferenciales.
Tanto las ecuaciones de Fredholm como las de Volterra, son ejemplos de ecuaciones integrales lineales, debido a la linealidad de la integral respecto a la función incógnita φ(x) situada bajo la integral. Un ejemplo de ecuación lineal de Volterra no lineal tendría la forma general:
Donde F es una función conocida.
Ecuaciones integrales como ecuaciones de valores propios
Algunas ecuaciones integrales lineales homogéneas pueden entenderse como el límite continuo de un problema de valores propios, usando la notación de índices, una ecuación de valores propios en un espacio vectorial de dimensión finita puede escribirse como:
Donde  es una matriz y
es una matriz y  uno de sus vectores propios asociado al valor propio
uno de sus vectores propios asociado al valor propio  .
.
 es una matriz y
es una matriz y  uno de sus vectores propios asociado al valor propio
uno de sus vectores propios asociado al valor propio  .
.
Haciendo el límite continuo mediante el cambio de los índices discretos  y
y  por los índices continuos
por los índices continuos  y
y se tiene:
se tiene:
 y
y  por los índices continuos
por los índices continuos  y
y se tiene:
se tiene:
Donde la suma sobre  ha sido substituida por una integral sobre
ha sido substituida por una integral sobre  y la matriz
y la matriz  y el vector
y el vector 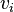 han sido substituidos por el "núcleo integral"
han sido substituidos por el "núcleo integral"  y la autofunción
y la autofunción  (los límites de la integral son fijos de manera análoga a la suma sobre
(los límites de la integral son fijos de manera análoga a la suma sobre  ).
).
 ha sido substituida por una integral sobre
ha sido substituida por una integral sobre  y la matriz
y la matriz  y el vector
y el vector 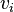 han sido substituidos por el "núcleo integral"
han sido substituidos por el "núcleo integral"  y la autofunción
y la autofunción  (los límites de la integral son fijos de manera análoga a la suma sobre
(los límites de la integral son fijos de manera análoga a la suma sobre  ).
).
En general,  puede ser una distribución o función generalizada, más que una función ordinaria. Si la distribución
puede ser una distribución o función generalizada, más que una función ordinaria. Si la distribución  tiene soporte sólo en el punto
tiene soporte sólo en el punto 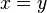 , entonces la ecuación integral se reduce a una ecuación diferencial de autovalores.
, entonces la ecuación integral se reduce a una ecuación diferencial de autovalores.
 puede ser una distribución o función generalizada, más que una función ordinaria. Si la distribución
puede ser una distribución o función generalizada, más que una función ordinaria. Si la distribución  tiene soporte sólo en el punto
tiene soporte sólo en el punto 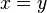 , entonces la ecuación integral se reduce a una ecuación diferencial de autovalores.
, entonces la ecuación integral se reduce a una ecuación diferencial de autovalores.Ecuaciones diferenciales reducidas a ecuaciones integrales
La formulación de muchos problemas matemáticos y físicos puede plantearse directamente en forma de ecuación integral. Incluso en ocasiones puede interesar convertir una ecuación diferencial en una ecuación integral equivalente, con la ventaja de que la ecuación integral, aparte de incluir las condiciones de contorno, maneja un operador acotado (de hecho, frecuenemente, un operador compacto), mientras que el operador diferencial era en general no acotado. Esto último permite echar mano de varios resultados conocidos para operadores compactos para resolver un problema planteado en términos de ecuaciones integrales.
Problemas de valor inicial
Dadas tres funciones  definidas en el intervalo [a, b], el problema de valor inicial siguiente:
definidas en el intervalo [a, b], el problema de valor inicial siguiente:
 definidas en el intervalo [a, b], el problema de valor inicial siguiente:
definidas en el intervalo [a, b], el problema de valor inicial siguiente:(1a)
puede convertirse en una ecuación integral integrando entre a y x y usando los valores iniciales en el punto a:
Integrando otra vez más:
Utilizando las siguientes identidades y definiciones:
La ecuación () puede escribirse como ecuación integral de Volterra de segunda clase:
(1b)
Para una ecuación de orden n con condiciones iniciales:
se tiene una misma forma pero la forma para g0(x) y k(x,y) es más complicada.
Problemas de contorno
De manera similar al caso anterior, dadas tres funciones  definidas en el intervalo [a, b], el problema de contorno siguiente:
definidas en el intervalo [a, b], el problema de contorno siguiente:
 definidas en el intervalo [a, b], el problema de contorno siguiente:
definidas en el intervalo [a, b], el problema de contorno siguiente:(2a)
Puede expresarse como ecuación integral de tipo Fredholm:
(2b)
Donde:
![g_0(x):=k_a \int_a^x (x-s)g(s)ds + \frac{x-a}{b-a}
\left[k_b-k_a - \int_a^b (b-s)g(s)ds \right]](https://upload.wikimedia.org/math/a/6/f/a6f935f92be770d5e387b7f9efb92519.png)
![k(x,y) = \begin{cases} \cfrac{x-a}{b-a}
[\alpha(y)-(b-y)(\alpha'(y)-\beta(y))] & x<y \\
\cfrac{x-b}{b-a}\alpha(y)+ [\alpha'(y)-\beta(y))]\cfrac{(y-a)(x-b)}{b-a}
& y>x \end{cases}](https://upload.wikimedia.org/math/9/b/7/9b72fc708c5387f93ecdaf1af62106ea.png)
- ecuación de Ornstein-Zernike (llamada así en honor de Leonard Ornstein y Frits Zernike) es una ecuación integral para definir la función de correlación directa. Básicamente describe la forma en que puede calcularse la correlación entre dos moléculas. Sus aplicaciones se encuentran principalmente en teoría de fluidos.
- La derivación presentada aquí es de naturaleza heurística; una derivación rigurosa requiere de extensivos análisis gráficos o técnicas funcionales.N. 1Es conveniente definir la función de correlación total:que es una medida de la «influencia» de la molécula 1 sobre la molécula 2, separadas una distancia r12, con g(r12) la función de distribución radial. En 1914, Ornstein y Zernike propusieron separar esta influencia en dos contribuciones: una directa y una indirecta.1La contribución directa está definida como dada por la función de correlación directa, denotada por c(r12). La parte indirecta es debida a la influencia de la molécula 1 sobre una tercera molécula, etiquetada con 3, la cual, a su vez, afecta a la molécula 2, directa e indirectamente. Este efecto indirecto se pondera con la densidad y se promedia sobre todas las posibles posiciones de la partícula 3. Esta descomposición puede escribirse matemáticamente comoLa ecuación anterior es conocida como ecuación de Ornstein–Zernike. Su interés es que, al eliminar la influencia indirecta, c(r) actúa a distancias menores que h(r) y puede ser descrita más fácilmente.Si definimos el vector de distancia entre dos moléculas comorij ≡ ri − rj para i,j = 1,2,3, la ecuación de Ornstein-Zernike puede reescribirse usando una convolución.
-
 .
.
Si ahora denotamos las transformada de Fourier de h(r) y de c(r) como Ĥ(k) y Ĉ(k), respectivamente, y utilizamos el teorema de convolución, obtenemos:lo cual conduce aEs necesario resolver tanto para h(r) como para c(r) (o, de forma equivalente, para sus transformadas de Fourier). Esto requiere de una ecuación adicional conocida como relación de cerradura. La ecuación de Ornstein–Zernike puede verse formalmente como una definición de la función de correlación directa c(r) en términos de la función de correlation total h(r). Los detalles del sistema que se esté estudiando —principalmente la forma del potencial de interacción u(r)— deben ser tomados en cuenta al escoger la relación de cerradura. Comúnmente se utilizan las relaciones de cerradura de la aproximación de Percus-Yevick, que se adapta bien a partículas con núcleo impenetrable, y la ecuación de cadena hipertejida, muy usada para potenciales más «suaves». -
- ecuaciones integrales de Volterra son un tipo de ecuaciones integrales especiales. Están divididas en dos grupos: de primer y segundo tipo.Una ecuación de Volterra lineal de primer tipo es:
 Una ecuación de Volterra lineal de segundo tipo es:
Una ecuación de Volterra lineal de segundo tipo es: En teoría de operaciones, y en la teoría de Fredholm, las ecuaciones correspondientes son denominadas operadores de Volterra.Una ecuación integral de Volterra lineal es una ecuación de convoluciones si:
En teoría de operaciones, y en la teoría de Fredholm, las ecuaciones correspondientes son denominadas operadores de Volterra.Una ecuación integral de Volterra lineal es una ecuación de convoluciones si: La función
La función en la integral es a menudo llamada kernel. Tales ecuaciones pueden ser analizadas y resueltas por los métodos de latransformada de Laplace.Las ecuaciones integrales de Volterra fueron presentadas por el físico y matemático italiano Vito Volterra (1860–1940) y luego estudiadas por Traian Lalescu en su tesis de 1908, Sur les équations de Volterra, escritas bajo la dirección de Émile Picard. En 1911, Lalescu escribió el primer libro de ecuaciones integrales de la historia.Las ecuaciones integrales de Volterra encuentran aplicación en demografía, el estudio de los materiales viscoelásticos y en matemáticas de seguros a través de la ecuación de renovación.
en la integral es a menudo llamada kernel. Tales ecuaciones pueden ser analizadas y resueltas por los métodos de latransformada de Laplace.Las ecuaciones integrales de Volterra fueron presentadas por el físico y matemático italiano Vito Volterra (1860–1940) y luego estudiadas por Traian Lalescu en su tesis de 1908, Sur les équations de Volterra, escritas bajo la dirección de Émile Picard. En 1911, Lalescu escribió el primer libro de ecuaciones integrales de la historia.Las ecuaciones integrales de Volterra encuentran aplicación en demografía, el estudio de los materiales viscoelásticos y en matemáticas de seguros a través de la ecuación de renovación.



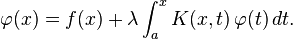


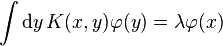

![f'(x) -k_1 = \alpha(x)f(x)-\int_a^x [\beta(s)-\alpha'(s)]f(s)ds +
\int_a^x g(s)ds + \alpha(a)k_0](https://upload.wikimedia.org/math/6/5/4/6549d652af84e95e89593855e5965c66.png)
![f(x) = -\int_a^x \alpha(y)f(y)dy - \int_a^x dy\int_a^y [\beta(s)-\alpha'(s)]f(s)ds +
\int_a^x dy \int_a^y g(s)ds + [\alpha(a)k_0 + k_1](x-a) + k_0](https://upload.wikimedia.org/math/d/d/f/ddf9aa8648a2c187efa4524c8c10ddd2.png)
+k_0 \\
k(x,y):= -\alpha(x)-(x-y)[\beta(y)-\alpha'(y)] \end{cases}](https://upload.wikimedia.org/math/3/f/f/3ff78c3d183c4cc41163513366ece09b.png)






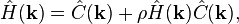
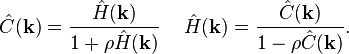
No hay comentarios:
Publicar un comentario