sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas que conforman un problema matemático que consiste enencontrar los valores de las incógnitas que satisfacen dichas ecuaciones.
En un sistema de ecuaciones algebraicas las incógnitas son valores numéricos menores a la constante (o más generalmente elementos de un cuerpo sobre el que se plantean las ecuaciones), mientras que en una ecuación diferencial las incógnitas son funciones o distribuciones de un cierto conjunto definido de antemano. Una solución de dicho sistema es por tanto, un valor o una función que substituida en las ecuaciones del sistema hace que éstas se cumplan automáticamente sin que se llegue a una contradicción. En otras palabras el valor que reemplazamos en las incógnitas debe hacer cumplir la igualdad del sistema.
Las incógnitas se suelen representar utilizando las últimas letras del alfabeto latino, o si son demasiadas, con subíndices.
Sistema general
La forma genérica de un sistema de  ecuaciones algebraicas y
ecuaciones algebraicas y  incógnitas es la siguiente:
incógnitas es la siguiente:
 ecuaciones algebraicas y
ecuaciones algebraicas y  incógnitas es la siguiente:
incógnitas es la siguiente:(1)
donde  son funciones de las incógnitas. La solución, perteneciente al espacio euclídeo
son funciones de las incógnitas. La solución, perteneciente al espacio euclídeo  , será tal que el resultado de evaluar cualquier expresión
, será tal que el resultado de evaluar cualquier expresión 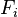 con los valores de dicha solución, verifique la ecuación.
con los valores de dicha solución, verifique la ecuación.
 son funciones de las incógnitas. La solución, perteneciente al espacio euclídeo
son funciones de las incógnitas. La solución, perteneciente al espacio euclídeo  , será tal que el resultado de evaluar cualquier expresión
, será tal que el resultado de evaluar cualquier expresión 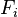 con los valores de dicha solución, verifique la ecuación.
con los valores de dicha solución, verifique la ecuación.Representación gráfica
Los sistemas de 2 o 3 incógnitas reales admiten representaciones gráficas cuando las funciones 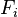 en () son continuas a tramos. En cada ecuación se representa como una curva o una superficie curva. La existencia de soluciones en ese caso puede deducirse a partir de la existencia de intersecciones comunes a dichas curvas o superficies curvas.
en () son continuas a tramos. En cada ecuación se representa como una curva o una superficie curva. La existencia de soluciones en ese caso puede deducirse a partir de la existencia de intersecciones comunes a dichas curvas o superficies curvas.
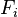 en () son continuas a tramos. En cada ecuación se representa como una curva o una superficie curva. La existencia de soluciones en ese caso puede deducirse a partir de la existencia de intersecciones comunes a dichas curvas o superficies curvas.
en () son continuas a tramos. En cada ecuación se representa como una curva o una superficie curva. La existencia de soluciones en ese caso puede deducirse a partir de la existencia de intersecciones comunes a dichas curvas o superficies curvas.Clasificación de los sistemas
Un sistema de ecuaciones sobre  puede clasificarse de acuerdo con el número de soluciones o cardinal del conjunto de soluciones
puede clasificarse de acuerdo con el número de soluciones o cardinal del conjunto de soluciones 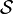 , de acuerdo con este criterio un sistema puede ser:
, de acuerdo con este criterio un sistema puede ser:
 puede clasificarse de acuerdo con el número de soluciones o cardinal del conjunto de soluciones
puede clasificarse de acuerdo con el número de soluciones o cardinal del conjunto de soluciones 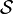 , de acuerdo con este criterio un sistema puede ser:
, de acuerdo con este criterio un sistema puede ser:- Sistema compatible cuando admite alguna solución que a su vez pueden dividirse en:
- Sistemas compatibles determinados cuando admiten un conjunto finito de soluciones, o un conjunto infinito de soluciones aisladas sin puntos de acumulación,
 .
. - Sistemas compatibles indeterminados cuando existe un número infinito de soluciones que forman unavariedad continua,
 .
.
- Sistemas compatibles determinados cuando admiten un conjunto finito de soluciones, o un conjunto infinito de soluciones aisladas sin puntos de acumulación,
- Sistema incompatible cuando no admite ninguna solución,
 .
.
Sistema lineal general
Se llama sistema lineal si las ecuaciones que conforman el sistema son funciones afines. A diferencia del caso general, la solución de los sistemas de ecuaciones lineales son fáciles de encontrar cuando los coeficientes de las ecuaciones son números reales o complejos. También existen medios generales de resolución cuando los coeficientes pertenecen a un anillo, aunque la búsqueda de las soluciones en ese caso puede ser un poco más complicada.
Una característica importante de los sistemas lineales de ecuaciones es que admiten la llamada forma matricial. Esta forma permite representar el sistema usando tresmatrices, de la siguiente forma:
(2)
La primera es la matriz de coeficientes, donde el término  representa al coeficiente que acompaña a la j-ésima incógnita de la ecuación i-ésima. La segunda es la matriz de incógnitas, donde cada término se corresponde con una de las
representa al coeficiente que acompaña a la j-ésima incógnita de la ecuación i-ésima. La segunda es la matriz de incógnitas, donde cada término se corresponde con una de las  incógnitas. La tercera matriz es la de términos independientes, donde el cada
incógnitas. La tercera matriz es la de términos independientes, donde el cada 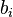 representa al término independiente de la ecuación i-ésima.
representa al término independiente de la ecuación i-ésima.
 representa al coeficiente que acompaña a la j-ésima incógnita de la ecuación i-ésima. La segunda es la matriz de incógnitas, donde cada término se corresponde con una de las
representa al coeficiente que acompaña a la j-ésima incógnita de la ecuación i-ésima. La segunda es la matriz de incógnitas, donde cada término se corresponde con una de las  incógnitas. La tercera matriz es la de términos independientes, donde el cada
incógnitas. La tercera matriz es la de términos independientes, donde el cada 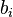 representa al término independiente de la ecuación i-ésima.
representa al término independiente de la ecuación i-ésima.
Esta representación matricial facilita el uso de algunos métodos de resolución, como el método de Gauss, en el que, partiendo de la matriz aumentada (matriz de coeficientes a la que se le ha acoplado la matriz de términos independientes), y aplicando transformaciones lineales sobre las ecuaciones, se pretende llegar a una matriz de este tipo:
Una vez que la matriz se ha triangulado, el valor de cada término 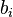 se corresponderá con el de la incógnita
se corresponderá con el de la incógnita 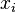 . Si queda alguna fila del tipo
. Si queda alguna fila del tipo 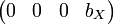 , con
, con  , el sistema no tendrá solución.
, el sistema no tendrá solución.
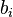 se corresponderá con el de la incógnita
se corresponderá con el de la incógnita 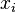 . Si queda alguna fila del tipo
. Si queda alguna fila del tipo 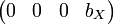 , con
, con  , el sistema no tendrá solución.
, el sistema no tendrá solución.
Ejemplos:
- Un sistema lineal incompatible es
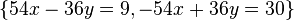 , ya que usando el método reducción y sumando miembro a miembro se obtiene la contradicción 0 = 39.
, ya que usando el método reducción y sumando miembro a miembro se obtiene la contradicción 0 = 39. - Un ejemplo de sistema lineal compatible indeterminado es
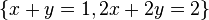 ya que claramente la segunda ecuación es linealmente dependiente de la primera, habiéndo sido multiplicados todos los términos por 2.
ya que claramente la segunda ecuación es linealmente dependiente de la primera, habiéndo sido multiplicados todos los términos por 2. - Un ejemplo de sistema lineal compatible determinado es
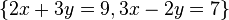 cuya solución única es
cuya solución única es  y
y 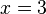 .
.
Existencia de soluciones
El teorema de la función inversa proporciona condiciones suficientes de existencia de solución, de un sistema como () con 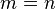 . Si sucede que la función vectorial:
. Si sucede que la función vectorial:
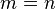 . Si sucede que la función vectorial:
. Si sucede que la función vectorial:
es diferenciable con continuidad, es decir, es de clase 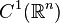 y su jacobiano no se anula en ningún punto entonces existe una única solución del sistema (). En ese caso existirá una función inversa, y se podrá escribir la solución buscada simplemente como:
y su jacobiano no se anula en ningún punto entonces existe una única solución del sistema (). En ese caso existirá una función inversa, y se podrá escribir la solución buscada simplemente como:
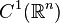 y su jacobiano no se anula en ningún punto entonces existe una única solución del sistema (). En ese caso existirá una función inversa, y se podrá escribir la solución buscada simplemente como:
y su jacobiano no se anula en ningún punto entonces existe una única solución del sistema (). En ese caso existirá una función inversa, y se podrá escribir la solución buscada simplemente como:
Sin embargo, la condición de diferenciabilidad anterior aún siendo condición suficiente, no es una condición necesaria, por lo que existen sistemas de ecuaciones en que las funciones 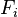 no son diferenciables y sin embargo, existen soluciones. Más aún, en casos en que existe más de una solución, si la función es diferenciable entonces el jacobiano se anula en algún punto, pero eso no impide que existan varias soluciones.
no son diferenciables y sin embargo, existen soluciones. Más aún, en casos en que existe más de una solución, si la función es diferenciable entonces el jacobiano se anula en algún punto, pero eso no impide que existan varias soluciones.
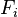 no son diferenciables y sin embargo, existen soluciones. Más aún, en casos en que existe más de una solución, si la función es diferenciable entonces el jacobiano se anula en algún punto, pero eso no impide que existan varias soluciones.
no son diferenciables y sin embargo, existen soluciones. Más aún, en casos en que existe más de una solución, si la función es diferenciable entonces el jacobiano se anula en algún punto, pero eso no impide que existan varias soluciones.
En casos de un menor número de ecuaciones que de incógnitas, cuando  , entonces el sistema es compatible indeterminado o carece de soluciones. En esos casos, el teorema de la función implícita proporciona condiciones suficientes, aunque no necesarias, para la existencia de soluciones de un modo similar a como el teorema de la función inversa las proporciona en el caso
, entonces el sistema es compatible indeterminado o carece de soluciones. En esos casos, el teorema de la función implícita proporciona condiciones suficientes, aunque no necesarias, para la existencia de soluciones de un modo similar a como el teorema de la función inversa las proporciona en el caso 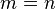 .
.
 , entonces el sistema es compatible indeterminado o carece de soluciones. En esos casos, el teorema de la función implícita proporciona condiciones suficientes, aunque no necesarias, para la existencia de soluciones de un modo similar a como el teorema de la función inversa las proporciona en el caso
, entonces el sistema es compatible indeterminado o carece de soluciones. En esos casos, el teorema de la función implícita proporciona condiciones suficientes, aunque no necesarias, para la existencia de soluciones de un modo similar a como el teorema de la función inversa las proporciona en el caso 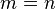 .
.Número de soluciones
En un sistema de ecuaciones lineales compatible y determinado la solución es siempre única. En el caso de ecuaciones polinómicas la respuesta es más complicada, aunque puede probarse que dos curvas polinómicas en el plano de grados n y m funcionalmente independientes tienen como mucho nm soluciones diferentes. Ese resultado se desprende del siguiente teorema de Bézout:
- Dos curvas del plano proyectivo complejo
 , de grados n y m sin componentes comunes se cortan exactamente en mn puntos contados con multiplicidad.
, de grados n y m sin componentes comunes se cortan exactamente en mn puntos contados con multiplicidad.
Métodos de resolución
Si bien para los sistemas de ecuaciones lineales existen multitud de técnicas del álgebra lineal, para los sistemas de ecuaciones no lineales el problema es técnicamente más difícil.
Métodos analíticos
Los métodos analíticos se restringen casi exclusivamente a sistemas de ecuaciones lineales. Ni siquiera se conoce una solución analítica para el sistema de ecuaciones de segundo grado general:
Métodos numéricos
Las aplicaciones técnicas generalmente recurren a algoritmos numéricos que permiten calcular aproximaciones numéricas a las soluciones de un sistema de ecuaciones.
Uno de los métodos numéricos que puede generalizarse a sistemas no lineales es el método de Newton-Raphson. En el caso multidimensional la resolución numérica del sistema de n ecuaciones 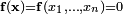 puede hacerse a partir del conocimiento de una solución aproximada
puede hacerse a partir del conocimiento de una solución aproximada  , siempre y cuando la aplicación anterior sea diferenciable, mediante el esquema iterativo:
, siempre y cuando la aplicación anterior sea diferenciable, mediante el esquema iterativo:
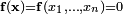 puede hacerse a partir del conocimiento de una solución aproximada
puede hacerse a partir del conocimiento de una solución aproximada  , siempre y cuando la aplicación anterior sea diferenciable, mediante el esquema iterativo:
, siempre y cuando la aplicación anterior sea diferenciable, mediante el esquema iterativo:
O más explícitamente:
Lamentablemente la convergencia del esquema iterativo anterior no está garantizada y en casos de soluciones múltiples la convergencia puede darse hacia la solución no deseada.
Métodos gráficos
Los métodos gráficos son didácticos e ilustrativos, aunque en general carecen de interés práctico en las aplicaciones
Dos sistemas de ecuaciones con dos incógnitas de valor real, suelen aparecer como uno de los cinco tipos diferentes mencionados a continuación. Tienen una relación con el número de soluciones:
- Aquellos sistemas de ecuaciones que representan gráficamente rectas y curvas que se intersecan entre sí. Este tipo de sistema de ecuación es considerado como el normal. Suele tener un número de soluciones finito cada uno formado por las coordenadas de los punto de intersección.
- Sistemas que tienen simplificaciones falsas. Por ejemplo: 1 = 0. Gráficamente se representan como un conjunto de líneas que nunca se intersecan entre sí, como líneas paralelas.
- Sistemas de ecuaciones en las que ambos simplificar a una identidad (por ejemplo, x = 2x - y o y - x = 0). Cualquier asignación de valores a las variables desconocidas satisface las ecuaciones. Por lo tanto, hay un número infinito de soluciones, que gráficamente, se representa como todos los puntos del plano que representa la solución.
- Sistemas en los que las dos ecuaciones representan el mismo conjunto de puntos: son matemáticamente equivalentes (una ecuación general puede ser transformada en otra a través de la manipulación algebraica). Estos sistemas representan completamente la superposición de líneas o curvas, etc Una de las dos ecuaciones es redundante y puede ser desechada. Cada punto de la serie de puntos corresponde a una solución. Generalmente, esto significa que hay un número infinito de soluciones.
- Sistemas en los que una (y sólo una) de las dos ecuaciones se simplifica a una identidad. Por lo tanto, es redundante y puede ser descartada, según el tipo anterior. Cada punto de la serie de puntos representados por los demás es una solución de la ecuación de los que hay a continuación, por lo general un número infinito.
La ecuación x2 + y2 = 0 puede ser pensada como la ecuación de un círculo cuyo radio se ha reducido a cero, por lo que representa un único punto: (x = 0, y = 0), a diferencia de una normal de un círculo que contiene infinito número de puntos. Este y otros casos similares muestran la razón por la cual los dos últimos tipos anteriormente descritos necesitan la calificación de "normalmente". Un ejemplo de un sistema de ecuaciones del primer tipo descrito anteriormente, con un número infinito de soluciones viene dada por x = | x |, y = | y | (donde la notación | • | indica el valor absoluto de la función), cuyas soluciones de forma un cuadrante de la x - y plano. Otro ejemplo es x = | y |, y = | x |, cuya solución representa un rayo.
sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
El problema consiste en encontrar los valores desconocidos de las variables x1, x2 y x3 que satisfacen las tres ecuaciones.
El problema de los sistemas lineales de ecuaciones es uno de los más antiguos de la matemática y tiene una infinidad de aplicaciones, como en procesamiento digital de señales, análisis estructural, estimación, predicción y más generalmente en programación lineal así como en la aproximación de problemas no lineales de análisis numérico.
Introducción
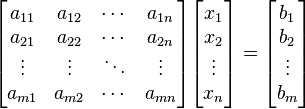
En general, un sistema con m ecuaciones lineales y n incógnitas puede ser escrito en forma normal como:
Donde  son las incógnitas y los números
son las incógnitas y los números 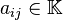 son los coeficientes del sistema sobre el cuerpo
son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](https://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . Es posible reescribir el sistema separando con coeficientes con notación matricial:
. Es posible reescribir el sistema separando con coeficientes con notación matricial:
 son las incógnitas y los números
son las incógnitas y los números 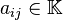 son los coeficientes del sistema sobre el cuerpo
son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](https://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . Es posible reescribir el sistema separando con coeficientes con notación matricial:
. Es posible reescribir el sistema separando con coeficientes con notación matricial:(1)
Si representamos cada matriz con una única letra obtenemos:
Donde A es una matriz m por n, x es un vector columna de longitud n y b es otro vector columna de longitud m. El sistema de eliminación de Gauss-Jordan se aplica a este tipo de sistemas, sea cual sea el cuerpo del que provengan los coeficientes. La matriz A se llama matriz de coeficientes de este sistema lineal. A b se le llama vector de términos independientes del sistema y a x se le llama vector de incógnitas.
Sistemas lineales reales
En esta sección se analizan las propiedades de los sistemas de ecuaciones lineales sobre el cuerpo  , es decir, los sistemas lineales en los cuales los coeficientes de las ecuaciones son números reales.
, es decir, los sistemas lineales en los cuales los coeficientes de las ecuaciones son números reales.
 , es decir, los sistemas lineales en los cuales los coeficientes de las ecuaciones son números reales.
, es decir, los sistemas lineales en los cuales los coeficientes de las ecuaciones son números reales.Representación gráfica
Un sistema con  incógnitas se puede representar en el n-espacio correspondiente.
incógnitas se puede representar en el n-espacio correspondiente.
 incógnitas se puede representar en el n-espacio correspondiente.
incógnitas se puede representar en el n-espacio correspondiente.
En los sistemas con 2 incógnitas, el universo de nuestro sistema será el plano bidimensional, mientras que cada una de las ecuacionesserá representada por una recta. La solución será el punto (o línea) donde se intersequen todas las rectas representan a las ecuaciones. Si no existe ningún punto en el que se intersequen al mismo tiempo todas las líneas, el sistema es incompatible, o lo que es lo mismo, no tiene solución.
En el caso de un sistema con 3 incógnitas, el universo será el espacio tridimensional, siendo cada ecuación un plano dentro del mismo. Si todos los planos intersecan en un único punto, las coordenadas de este serán la solución al sistema. Si, por el contrario, la intersección de todos ellos es una recta o incluso un plano, el sistema tendrá infinitas soluciones, que serán las coordenadas de los puntos que forman dicha línea o superficie.
Para sistemas de 4 o más incógnitas, la representación gráfica no existe, por lo que dichos problemas no se enfocan desde esta óptica.
Tipos de sistemas
Los sistemas de ecuaciones se pueden clasificar según el número de soluciones que pueden presentar. De acuerdo con ese caso se pueden presentar los siguientes casos:
- Sistema compatible si tiene solución, en este caso además puede distinguirse entre:
- Sistema compatible determinado cuando tiene una única solución.
- Sistema compatible indeterminado cuando admite un conjunto infinito de soluciones.
- Sistema incompatible si no tiene solución.
Quedando así la clasificación:
Los sistemas incompatibles geométricamente se caracterizan por (hiper)planos o rectas que se cruzan sin cortarse. Los sistemas compatibles determinados se caracterizan por un conjunto de (hiper)planos o rectas que se cortan en un único punto. Los sistemas compatibles indeterminados se caracterizan por (hiper)planos que se cortan a lo largo de una recta [o más generalmente un hiperplano de dimensión menor]. Desde un punto de vista algebraico los sistemas compatibles determinados se caracterizan porque el determinante de la matriz es diferente de cero:
Algoritmo para determinar si un sistema es compatible
Podemos averiguar si un sistema es o no compatible mediante el Teorema de Rouché-Frobenius que establece que un sistema de ecuaciones lineales es compatible sólo si el rango de su matriz ampliada coincide con el de su matriz de coeficientes. Supongamos que el sistema es compatible. Si el valor común de los rangos de las matrices coincide con el número de variables, el sistema es compatible determinado; en caso contrario, es compatible indeterminado.
Sistemas compatibles indeterminados
Un sistema sobre un cuerpo K es compatible indeterminado cuando posee un número infinito de soluciones. Por ejemplo, el siguiente sistema:
Tanto la primera como la segunda ecuación se corresponden con la recta cuya pendiente es  y que pasa por el punto
y que pasa por el punto  , por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.
, por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.
 y que pasa por el punto
y que pasa por el punto  , por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.
, por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.- En este tipo de sistemas, la solución genérica consiste en expresar una o más variables como función matemática del resto. En los sistemas lineales compatibles indeterminados, al menos una de sus ecuaciones se puede hallar como combinación lineal del resto, es decir, es linealmente dependiente.
- La condición necesaria para que un sistema sea compatible indeterminado es que el determinante de la matriz del sistema sea cero al igual que el rango de la matriz ampliada y menor al número de incógnitas(y por tanto uno de sus autovalores será 0):
- De hecho, de las dos condiciones anteriores se desprende, que el conjunto de soluciones de un sistema compatible indeterminado es un subespacio vectorial. Y la dimensión de ese espacio vectorial coincidirá con la multiplicidad geométrica del autovalor cero.
Sistemas incompatibles
De un sistema se dice que es incompatible cuando no presenta ninguna solución. Por ejemplo, supongamos el siguiente sistema:
Las ecuaciones se corresponden gráficamente con dos rectas, ambas con la misma pendiente, Al ser paralelas, no se cortan en ningún punto, es decir, no existe ningún valor que satisfaga a la vez ambas ecuaciones.
Matemáticamente un sistema de estos es incompatible cuando el rango de la matriz del sistema es inferior al rango de la matriz ampliada. Una condición necesaria para que esto suceda es que el determinante de la matriz del sistema sea cero:
Métodos de solución a sistemas de ecuaciones lineales
Sustitución
El método de sustitución consiste en despejar en una de las ecuaciones con cualquier incógnita, preferiblemente la que tenga menor coeficiente y a continuación sustituirla en otra ecuación por su valor.
En caso de sistemas con más de dos incógnitas, la seleccionada debe ser sustituida por su valor equivalente en todas las ecuaciones excepto en la que la hemos despejado. En ese instante, tendremos un sistema con una ecuación y una incógnita menos que el inicial, en el que podemos seguir aplicando este método reiteradamente. Por ejemplo, supongamos que queremos resolver por sustitución este sistema:
En la primera ecuación, seleccionamos la incógnita  por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
 por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
El siguiente paso será sustituir cada ocurrencia de la incógnita  en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  .
.
 en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  .
.
Al resolver la ecuación obtenemos el resultado 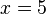 , y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos 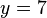 , con lo que el sistema queda ya resuelto.
, con lo que el sistema queda ya resuelto.
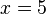 , y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos 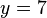 , con lo que el sistema queda ya resuelto.
, con lo que el sistema queda ya resuelto.Igualación
El método de igualación se puede entender como un caso particular del método de sustitución en el que se despeja la misma incógnita en dos ecuaciones y a continuación se igualan entre sí la parte derecha de ambas ecuaciones.
Tomando el mismo sistema utilizado como ejemplo para el método de sustitución, si despejamos la incógnita  en ambas ecuaciones nos queda de la siguiente manera:
en ambas ecuaciones nos queda de la siguiente manera:
 en ambas ecuaciones nos queda de la siguiente manera:
en ambas ecuaciones nos queda de la siguiente manera:
Como se puede observar, ambas ecuaciones comparten la misma parte izquierda, por lo que podemos afirmar que las partes derechas también son iguales entre sí.
Una vez obtenido el valor de la incógnita  , se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la
, se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la  .
.
 , se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la
, se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la  .
.
La forma más fácil de tener el método de sustitución es realizando un cambio para despejar x después de averiguar el valor de la y.
Reducción
Este método suele emplearse mayoritariamente en los sistemas lineales, siendo pocos los casos en que se utiliza para resolver sistemas no lineales. El procedimiento, diseñado para sistemas con dos ecuaciones e incógnitas, consiste en transformar una de las ecuaciones (generalmente, mediante productos), de manera que obtengamos dos ecuaciones en la que una misma incógnita aparezca con el mismo coeficiente y distinto signo. A continuación, se suman ambas ecuaciones produciéndose así la reducción o cancelación de dicha incógnita, obteniendo así una ecuación con una sola incógnita, donde el método de resolución es simple.
Por ejemplo, en el sistema:
No tenemos más que multiplicar la primera ecuación por 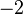 para poder cancelar la incógnita
para poder cancelar la incógnita  . Al multiplicar, dicha ecuación nos queda así:
. Al multiplicar, dicha ecuación nos queda así:
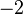 para poder cancelar la incógnita
para poder cancelar la incógnita  . Al multiplicar, dicha ecuación nos queda así:
. Al multiplicar, dicha ecuación nos queda así:
Si sumamos esta ecuación a la segunda del sistema original, obtenemos una nueva ecuación donde la incógnita  ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita
ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita  :
:
 ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita
ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita  :
:
El siguiente paso consiste únicamente en sustituir el valor de la incógnita  en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de
en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de  si sustituimos en la primera ecuación es igual a:
si sustituimos en la primera ecuación es igual a:
 en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de
en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de  si sustituimos en la primera ecuación es igual a:
si sustituimos en la primera ecuación es igual a:Método gráfico
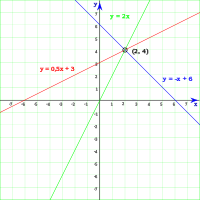
Consiste en construir la gráfica de cada una de las ecuaciones del sistema. El método (manualmente aplicado) solo resulta eficiente en el plano cartesiano, es decir para un espacio de dimensión .
El proceso de resolución de un sistema de ecuaciones mediante el método gráfico se resuelve en los siguientes pasos:
- Se despeja la incógnita en ambas ecuaciones.
- Se construye para cada una de las dos ecuaciones de primer grado obteniendo la tabla de valores correspondientes.
- Se representan gráficamente ambas rectas en los ejes coordenados.
- En este último paso hay tres posibilidades:
- Si ambas rectas se cortan, las coordenadas del punto de corte son los únicos valores de las incógnitas (x,y). "Sistema compatible determinado".
- Si ambas rectas son coincidentes, el sistema tiene infinitas soluciones que son las respectivas coordenadas de todos los puntos de esa recta en la que coinciden ambas. «Sistema compatible indeterminado».
- Si ambas rectas son paralelas, el sistema no tiene solución en los reales pero si en los complejos.
Método de Gauss
El método de eliminación de Gauss o simplemente método de Gauss consiste en convertir un sistema lineal de n ecuaciones con n incógnitas, en uno escalonado, en el que la primera ecuación tiene n incógnitas, la segunda ecuación tiene n - 1 incógnitas, ..., hasta la última ecuación, que tiene 1 incógnita. De esta forma, será fácil partir de la última ecuación e ir subiendo para calcular el valor de las demás incógnitas.
| Ejemplo de eliminación de Gauss |
Eliminación de Gauss-Jordan
Una variante de este método, denominada eliminación de Gauss-Jordan, es un método aplicable únicamente a los sistemas lineales de ecuaciones, y consistente en triangular la matriz aumentada del sistema mediante transformaciones elementales, hasta obtener ecuaciones de una sola incógnita, cuyo valor será igual al coeficiente situado en la misma fila de la matriz. Este procedimiento es similar al anterior de reducción, pero ejecutado de manera reiterada y siguiendo un cierto orden algorítmico.
| Ejemplo de eliminación de Gauss-Jordan |
Regla de Cramer
La regla de Cramer da una solución para sistemas compatibles determinados en términos de determinantes y adjuntos dada por:
Donde Aj es la matriz resultante de remplazar la j-ésima columna de A por el vector columna b. Para un sistema de dos ecuaciones y dos incógnitas:
La regla de Cramer da la siguiente solución:
Nota: Cuando en la determinante original det(A) el resultado es 0, el sistema indica múltiples o sin coincidencia.
Algoritmos numéricos
La eliminación de Gauss-Jordan es un algoritmo numérico usado para una gran cantidad de casos específicos, aunque posteriormente se han desarrollado algoritmos alternativos mucho más eficientes. La mayoría de estos algoritmos mejorados tienen una complejidad computacional de O(n²) (donde n es el número de ecuaciones del sistema). Algunos de los métodos más usados son:
- Para los problemas de la forma Ax = b, donde A es una matriz de Toeplitz simétrica, se puede utilizar la recursión de Levinson o alguno de los métodos derivados de este. Un método derivado de la recursión de Levinson es la recursión de Schur, que es ampliamente usado en el campo del procesamiento digital de señales.
- Para los problemas de la forma Ax = b, donde A es una matriz singular o casi singular, la matriz A se descompone en el producto de tres matrices en un proceso llamado descomposición en valores singulares.
Cuando consideramos ecuaciones lineales cuyas soluciones son números racionales, reales o complejos o más generalmente un cuerpo  , la solución puede encontrarse mediante Regla de Cramer. Para sistemas de muchas ecuaciones la regla de Cramer puede ser computacionalmente más costosa y suelen usarse otros métodos más "económicos" en número de operaciones como la eliminación de Gauss-Jordan y la descomposición de Cholesky. Existen también métodos indirectos (basados en iteraciones) como el método de Gauss-Seidel.
, la solución puede encontrarse mediante Regla de Cramer. Para sistemas de muchas ecuaciones la regla de Cramer puede ser computacionalmente más costosa y suelen usarse otros métodos más "económicos" en número de operaciones como la eliminación de Gauss-Jordan y la descomposición de Cholesky. Existen también métodos indirectos (basados en iteraciones) como el método de Gauss-Seidel.
 , la solución puede encontrarse mediante Regla de Cramer. Para sistemas de muchas ecuaciones la regla de Cramer puede ser computacionalmente más costosa y suelen usarse otros métodos más "económicos" en número de operaciones como la eliminación de Gauss-Jordan y la descomposición de Cholesky. Existen también métodos indirectos (basados en iteraciones) como el método de Gauss-Seidel.
, la solución puede encontrarse mediante Regla de Cramer. Para sistemas de muchas ecuaciones la regla de Cramer puede ser computacionalmente más costosa y suelen usarse otros métodos más "económicos" en número de operaciones como la eliminación de Gauss-Jordan y la descomposición de Cholesky. Existen también métodos indirectos (basados en iteraciones) como el método de Gauss-Seidel.
Si el cuerpo es infinito (como es el caso de los números reales o complejos), entonces solo puede darse una de las tres siguientes situaciones:
- el sistema no tiene solución (en dicho caso se dice que el sistema está sobredeterminado o que es incompatible)
- el sistema tiene una única solución (el sistema es compatible determinado)
- el sistema tiene un número infinito de soluciones (el sistema es compatible indeterminado).
Solución de sistemas lineales en un anillo
Los métodos para resolver el sistema () sobre un anillo son muy diferentes a los considerados anteriormente. De hecho la mayoría de métodos usados en cuerpos, como la regla de Cramer, son inaplicables en anillos debido a que no existen inversos multiplicativos.
La existencia de solución del sistema () sobre los enteros requiere varias condiciones:
- Para cada i
 es divisor de
es divisor de 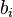 .
. - Si la condición anterior se cumple para un determinado i existe un conjunto de enteros
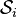 formado por el conjunto de enteros que satisface la i-ésima ecuación, y existirá solución si la intersección
formado por el conjunto de enteros que satisface la i-ésima ecuación, y existirá solución si la intersección  .
.
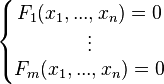



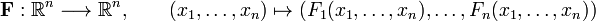

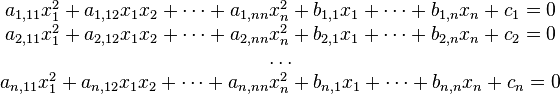
![\mathbf{x}^{(m+1)} = \mathbf{x}^{(m)} - [D\mathbf{f}(\mathbf{x}^{(m)})]^{-1}(\mathbf{f}(\mathbf{x}^{(m))}), \qquad \mathbf{f}:\R^n \to \R^n,\ \mathbf{f}\in C^{(1)}(\R^n;\R^n)](https://upload.wikimedia.org/math/8/f/b/8fb6bc36a0d7848d6c942dbd8a4ad727.png)
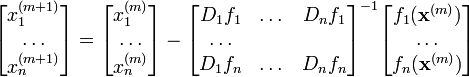
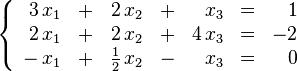
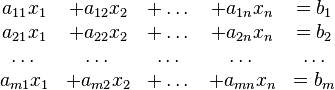
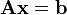

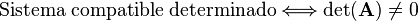



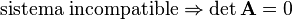

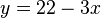
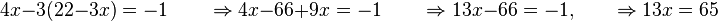
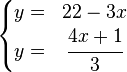


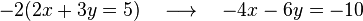

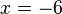
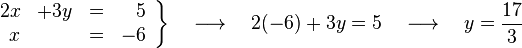



No hay comentarios:
Publicar un comentario