Electrodinámica cuántica
El positrón o antielectrón es una partícula elemental, antipartícula del electrón. Posee la misma cantidad de masa y carga eléctrica; sin embargo, ésta es positiva.2 No forma parte de la materia ordinaria, sino de la antimateria, aunque se producen en numerosos procesos radioquímicos como parte de transformaciones nucleares.
Esta partícula fue predicha por Paul Dirac en el año de 1928, para luego ser descubierta en el año 1932 por el físico norteamericano Anderson al fotografiar las huellas de los rayos cósmicos en una cámara de niebla.
En la actualidad, los positrones son rutinariamente producidos en la Tomografía por emisión de positrones usados en las instalaciones hospitalarias.
Creación de positrones por pulso láser
En noviembre de 2008 la doctora Hui Chen del Lawrence Livermore National Laboratory de Estados Unidos anunció que ella y su equipo habrían creado positrones al hacer incidir un breve aunque intenso pulso láser a través de una lámina de oro blanco de pocos milímetros de espesor, esto habría ionizado al material y acelerado sus electrones. Los electrones acelerados emitieron cuantos de energía que al decaer dieron lugar a partículas materiales y dando también por resultado positrones.3 (13 March 2009 issue of Physical Review Letters - Vol.102, No.10, article 105001)
El positrón en la ciencia ficción
- Sin duda el positrón adquirió fama en las diferentes novelas de robots de Isaac Asimov. Esta partícula era esencial para la fabricación de las sendas positrónicas en donde se programaría luego al robot, haciendo las veces de neuronas mecánicas. En conjunto las sendas se acoplaban y se posicionaban cuidadosamente en la cabeza del mismo. El autor admitió en vida que había tomado esta partícula como pilar de sus cerebros robóticos debido a que se había descubierto recientemente y eso atraería el interés de los lectores de la época.
Asimismo el positrón fue utilizado en diferentes series como fuente de energía de armas y poderes;
- En Digimon Adventure 02 el Digimon Imperialdramon utiliza un ataque conocido como "Láser Positrónico"
- En Neon Génesis Evangelion, de Hideaki Anno, el rifle positrónico es utilizado en varias ocasiones contra los ángeles invasores. Siendo el más notable Ramiel.
- En la nueva saga de Star Trek, el androide Data está construido con un cerebro positrónico.
- En la película El hombre bicentenario con el actor Robin Williams utiliza igualmente un cerebro del tipo positrónico.
- En todos los relatos de robots de ciencia-ficción de Isaac Asimov, los robots cuentan con un cerebro positrónico. Más tarde, el propio Asimov reconoció que no había pensado en llamar computador o procesador a dichos cerebros.
- En la Película GhostBusters los Científicos atrapa fantasmas usan rayos de positrones para atrapar a las criaturas ectoplasmicas.
| Positrón e+ | ||
|---|---|---|
 Fotografía en una cámara de niebla por C.D. Anderson, del primer positrón identificado. Una lámina de plomo de 6 mm separa la mitad superior de la cámara de la mitad inferior. El positrón debe haber venido de abajo ya que la parte superior de la pista se dobla con mayor fuerza en el campo magnético lo que indica una menor energía. | ||
| Clasificación | Partículas elementales | |
| Familia | Fermión | |
| Grupo | Leptón | |
| Generación | Primera | |
| Interacción | Gravedad, Electromagnetismo, Nuclear débil | |
| Símbolo(s) | β+, e+ | |
| Partícula | Electrón | |
| Teorizada | Paul Dirac (1928) | |
| Descubierta | Carl David Anderson (1932) | |
| Masa | 9,10938215 × 10−31 kg 1/1822,88849 uma | |
| Carga eléctrica | 1,602176487 × 10−19 C1 | |
| Momento magnético | −1.00115965218111 μB | |
| Carga de color | - | |
| Espín | ± 1/2 | |
EL POSITRÓN: DIRAC Y ANDERSON
N
OS encontramos a principios de 1932. Con el neutrón, recién descubierto, y el protón, conocemos a los constituyentes básicos del núcleo atómico. Si agregamos al electrón y al fotón, tenemos la impresión de haber, por fin, establecido la estructura básica de los átomos. ¿Se habría cumplido por fin el tan anhelado sueño? ¿Serían éstos todos los bloques elementales de la materia? En agosto del mismo año esta pregunta es respondida con el descubrimiento de la primer antipartícula, el positrón.
El positrón es un electrón con carga positiva. La interacción con el electrón puede resultar en la aniquilación de ambos, con lo que se produce un par de fotones cuya energía equivale a la masa del par electrón-positrón. Esta propiedad define al positrón como la antipartícula asociada al electrón. Los primeros indicios de la existencia del positrón surgieron, como veremos a continuación, del esfuerzo teórico por deducir la estructura electrónica del átomo.
Tan pronto como Rutherford descubrió el núcleo y propuso un modelo para el átomo en que los electrones giraban alrededor del núcleo, surgieron las objeciones. Un electrón, debido a que es una partícula cargada, cuando se mueve en torno al núcleo, bajo la acción de atracción de su carga eléctrica, debería irradiar ondas electromagnéticas, con lo que perdería energía. Así, en la concepción clásica de Maxwell, ese arreglo sería altamente inestable. El primero en introducir las ideas cuánticas a este problema fue Niels Bohr.
Niels Hendrik David Bohr nació en Dinamarca el 7 de octubre de 1885. Hijo de una familia de tradición universitaria y amplios medios económicos, Bohr ingresa a la Universidad de Copenhague en 1903, y permanece allí hasta obtener su doctorado en 1911. En marzo de 1912, Bohr visitó a Rutherford en su laboratorio de Manchester. Durante su estancia aprendió las técnicas experimentales usadas en radiactividad e inició trabajos sobre la estructura atómica, enfocándose originalmente a comprender la absorción de partículas en la materia. A finales de julio regresó a Copenhague, su ciudad natal. En abril de 1913 publicó el primer artículo en el que introduce las ideas de Planck sobre la cuantización para explicar las reglas espectrales empíricas derivadas anteriormente por Balmer para el átomo de hidrógeno (véase figura 6). Aunque el éxito de Bohr en este aspecto fue rotundo, sus ideas no fueron tomadas en serio inmediatamente, pues su formulación contenía varios postulados introducidos en forma un tanto arbitraria.
Figura 6. El átomo de Bohr. En un átomo de hidrógeno excitado, el electrón se encuentra en órbitas externas, decayendo a las más internas vía la emisión de la luz. La longitud de onda (l) correspondiente disminuye al aumentar la energía de la transición. Para una órbita inicial dada, las diversas alternativas de decaimiento forman una serie.
Para garantizar la estabilidad del átomo, Bohr propuso que los electrones sólo se mueven en órbitas estacionarias. Los únicos cambios energéticos del sistema son aquellos en que los electrones pasan de una órbita estacionaria a otra. El segundo postulado de Bohr indica que la radiación electromagnética esperada clásicamente para un electrón que gira alrededor del núcleo, sólo ocurre durante la transición entre órbitas estables y no mientras la estructura electrónica se mantenga inalterada. Con esto Bohr introducía una explicación para la observación de líneas espectrales bien definidas, en lugar del continuo de radiación predicho por el electromagnetismo de Maxwell.
Ya en 1921 el modelo de Bohr, mejorado por él mismo y por otros autores, describía al átomo como un arreglo de electrones que giran alrededor del núcleo en órbitas caracterizadas por tres numeros cuánticos, que determinan el número de cuantos de energía, de momento angular y su orientación. Tal modelo, sin embargo, no explicaba algunos fenómenos como el llamado efecto Zeeman anómalo.
Como se recordará, hacia fines del siglo
XIX Zeeman realizó un experimento para determinar el efecto del campo magnético sobre el espectro atómico. Lo que observó, con un equipo poco preciso, fue el ensanchamiento de las dos líneas espectrales del sodio. Lorentz interpretó que este fenómeno se debía a una descomposición de cada una de estas líneas primarias en tres, lo que reflejaba las posibles orientaciones del plano de la oscilación respecto al campo magnético. Esta predicción no pudo ser probada sino hasta un año después, en que Alfred Marie Cornu utilizó un equipo más complejo que el de Zeeman. Sin embargo, Cornu encontró que, si bien las líneas espectrales principales del sodio se subdividen, éstas lo hacen en seis y cuatro secundarias respectivamente y no en tres y tres como predijo Lorentz. Este fenómeno, conocido como efecto Zeeman anómalo,permaneció sin explicación hasta 1924, cuando el joven austriaco de 24 años Wolfgang Pauli le dio una explicación al postular la existencia de un cuarto número cuántico y de una nueva ley fundamental de la naturaleza: el principio de exclusión. Según éste, en el átomo no puede haber dos electrones con los mismos números cuánticos. Esto implica que cada órbita electrónica está poblada por un número máximo de electrones, dependiendo de su momento angular. Una predicción inmediata del modelo es la descomposición de las líneas espectrales del sodio en seis y cuatro, igual a lo observado por Cornu. Pauli recibió el Premio Nobel en 1945 por esta contribución.
En octubre de 1925 George Eugene Uhlembeck, nacido en 1900 en Sumatra en el seno de una familia holandesa, y Samuel Abraham Goudsmit, nacido en La Haya en 1902, propusieron el espín como una explicación para el cuarto número cuántico de Pauli. El equivalente clásico del espín es una rotación sobre sí mismo, similar al movimiento que ocasiona el día y la noche en la Tierra. Poco tiempo después del descubrimiento del electrón, George Francis Fitzgerald propuso que este tipo de rotación del electrón podría explicar el magnetismo. El electrón, visto como una esferita que gira sobre sí misma, se comporta como un giróscopo y, por estar cargada, también tendría las propiedades de un imán pues, como vimos anteriormente, una carga en movimiento genera un campo magnético a su alrededor.
La idea de Uhlembeck y Goudsmit fue introducida en forma un tanto arbitraria, ya que el electrón debía ser considerado como una esfera de dimensiones finitas. Si bien la idea fue perfeccionada en poco tiempo, permaneció como un agregado a la teoría cuántica no relativista que se desarrolló hasta entonces. Los efectos relativistas pueden ser despreciados siempre que la velocidad de una partícula sea muy inferior a la de la luz. Sin embargo, en el caso del electrón, debido a su masa tan pequeña, las fuerzas a que se encuentra sometido frecuentemente lo aceleran a velocidades cercanas a la de la luz. Otro problema conceptual de esta interpretación semiclásica del cuarto número cuántico de Pauli era que el espín del electrón debía ser sólo la mitad del mínimo momento angular orbital (diferente de cero), lo que permitía la mecánica cuántica.
La introducción de un momento angular semientero, o fraccionario, acarreaba una división interesante en el mundo cuántico, pues el comportamiento estadístico de sistemas de partículas con espín fraccionario, según descubrió el italiano Enrico Fermi en 1926 (Premio Nobel de 1939), resultaba ser diferente del de partículas con espín entero. En honor a aquél, a las partículas con espín fraccionario se les conoce genéricamente comofermiones. En contrapartida, la estadística de partículas con espín entero había sido estudiada por el hindú Satendra Nath Bose en 1924, en cuyo honor se denomina bosonesa ese tipo de partículas.
Hacia 1926, la necesidad de una formulación relativista para la mecánica cuántica era evidente y mantenía ocupados a algunos de los físicos teóricos más brillantes de la época. La primera descripción cuántico-relativista para el electrón fue lograda por Paul Adrien Maurice Dirac en Cambridge.
Dirac nació en Bristol, Inglaterra, en 1902, de padre suizo y madre inglesa. Empezó estudiando ingeniería eléctrica en su ciudad natal pero pronto se decidió por las matemáticas. En 1925, ya en Cambridge, se interesó por la teoría cuántica, recientemente desarrollada por Heisenberg. Su habilidad matemática le permitió plantear una formulación nueva de la mecánica cuántica que publicó ese mismo año. En 1928 encontró una manera de escribir una ecuación cuántico-relativista para el electrón. De su derivación surgía automáticamente un grado de libertad con todas las características del espín. Tal predicción dio prestigio y respeto a la formulación de Dirac.
La teoría de Dirac permite calcular la energía del electrón, incluida su masa en reposo. Sin embargo, predecía la existencia de un conjunto de estados de energía negativa, idénticos al conjunto de estados de energía positiva que él se proponía encontrar. Esto fue visto, inicialmente, como un defecto de la teoría, pues sugería la existencia de una partícula idéntica al electrón pero de carga positiva que hasta entonces nadie había observado.
La presión sobre Dirac fue enorme. Heisenberg encontró que la formulación de Dirac había causado más confusión que orden y la calificó como "el capítulo más triste en la física moderna". Con el ánimo de dar una interpretación creíble a su teoría, Dirac propuso que tal partícula podría ser el protón, pero Hermann Weyl pronto hizo notar que la simetría de las ecuaciones implicaba que la tal partícula debería tener la misma masa del electrón. En 1930, Robert Oppenheimer se dio cuenta de que suponer que se trataba de protones, implicaba que el átomo de hidrógeno se aniquilaría en una fracción de segundo. Convencido, Dirac postuló en 1931 la existencia de electrones positivos como la única interpretación posible a su teoría.
Los electrones positivos se mantuvieron como un defecto en la teoría de Dirac hasta que el 2 de agosto de 1932 el norteamericano Carl David Anderson, del Instituto Tecnológico de California, al estudiar las trazas que los rayos cósmicos dejaban en sus sistemas de detección, observó lo que sería la primera evidencia irrevocable sobre los electrones positivos o positrones.
La existencia de rayos cósmicos había sido establecida durante la búsqueda de nuevas fuentes radiactivas en la naturaleza, tarea que se popularizó luego del descubrimiento de la radiactividad. Inicialmente, los investigadores se sorprendieron al encontrar radiaciones en todas las partes donde se las buscó, lagos, montañas, etc. La inevitabilidad de las radiaciones, aun cuando los detectores fueran protegidos por capas gruesas de plomo, resultaba inexplicable con base en el conocimiento sobre las fuentes terrestres, e hizo suponer a algunos investigadores que el origen de estas radiaciones, tan penetrantes, podría ser cósmico. Para comprobar esta hipótesis fue necesario medir la intensidad de esta radiación como función de la altura. Los primeros experimentos se limitaron a las edificaciones más altas, como la Torre Eiffel, pero los resultados no fueron muy concluyentes. El siguiente paso fue el uso de globos, con los que se llegaron a medir radiaciones hasta a 4 500 metros de altura, donde el nivel de radiación no parecía disminuir. Esta omnipresencia de la radiación ayudó a descartar las fuentes en la superficie de la Tierra como sus posibles generadoras.
Entre 1911 y 1912 el austriaco Victor Franz Hess investigó sistemáticamente este fenómeno y encontró que la radiación aumentaba a partir de los mil metros, y llegaba a ser el doble de lo medido en la superficie de la Tierra a cinco mil metros de altura. Hess propuso entonces que, en efecto, existe un flujo importante de radiaciones proveniente del espacio. La intensidad de estas radiaciones resultó estar poco correlacionada con el día o la noche, lo que llevó a suponer que el origen de estas radiaciones no era solar necesariamente.
La siguiente pregunta acerca de los rayos cósmicos se refería a su propia naturaleza. Siendo excepcionalmente penetrantes podría tratarse por ejemplo de algún tipo de radiación diferente de los a , b o g hasta entonces descubiertos en la Tierra. El método obvio para discernir entre partículas cargadas, positivas o negativas, y fotones, era hacer pasar la radiación cósmica por un campo magnético. La visualización de las trayectorias se haría a través de las trazas dejadas por las partículas en cámaras de Wilson. Como ya vimos, estos artefactos consisten en un tanque que contiene una atmósfera supersaturada de vapor. La radiación incidente interactúa con el medio causando ionización a lo largo de su trayectoria. La carga de estos iones atrae moléculas hasta formar gotitas. La imagen de las columnas de gotitas se puede fotografiar para permitir el análisis posterior de las trayectorias seguidas por los rayos incidentes. Desgraciadamente, los primeros experimentos de este tipo mostraban que la radiación incidente parecía no ser afectada por los campos magnéticos utilizados. Este hecho podía implicar que, o bien las partículas incidentes, aunque cargadas, poseían una energía tan alta que la curvatura de las trayectorias debida al campo magnético fuera imperceptible, o bien que se tratase de otro tipo de radiación. Este dilema sólo podría ser resuelto mediante la intensificación de los campos. Otro método que se estudió por aquellas fechas consistió en utilizar el campo magnético de la Tierra, y buscar alguna diferencia en la intensidad de la radiación cósmica entre el ecuador y los polos.
En 1930, Robert Andrews Millikan, el mismo que midiera la carga del electrón, decidió montar un experimento equipado con cámaras de Wilson e imanes más poderosos que los utilizados hasta entonces. Para dirigir este proyecto, Millikan escogió a Carl David Anderson.
Nacido en septiembre de 1905 en Nueva York, Anderson estudió física en el Instituto Tecnológico de California, donde se graduó en 1927, y obtuvo en la misma institución el doctorado bajo la dirección de Millikan en 1930. El montaje del experimento de los rayos cósmicos tomó más de un año, al cabo del cual se empezaron a tomar fotografías, día y noche, cada quince segundos.
El primer análisis de los resultados fue publicado en 1931. En su artículo, Anderson describía la aparición de varios tipos de radiación que podían ser interpretados como protones, núcleos más pesados y electrones. Por su mayor penetrabilidad y la marcada curvatura de sus trayectorias, los electrones podían ser identificados con gran facilidad en sus fotografías. Ocasionalmente, sin embargo, Anderson encontró evidencias de trayectorias muy similares a las de los electrones pero con una curvatura invertida, como si se tratara de partículas con carga positiva. Intrigado, Anderson mejoró sus técnicas y buscó evidencias más convincentes de la existencia de estas irregularidades. En agosto de 1932, obtuvo la primera imagen clara de una partícula que, luego de atravesar una placa de plomo, se detenía en la cámara de niebla. Por el tipo de trayectoria, debería tratarse de un electrón, sólo que su curvatura era inversa a la de una partícula negativa. Anderson, quien aparentemente no conocía la predicción de Dirac, publicó su resultado concluyendo que se trataba de un electrón positivo o positrón. Anderson fue laureado con el Premio Nobel por su descubrimiento en 1936. Compartió este premio con Franz Hess.
Aparentemente, Anderson no fue el primero en tener evidencias sobre el positrón. Anteriormente Bruno Rossi realizó un experimento en el que medían eventos coincidentes en tres detectores Geiger-Muller. Las coincidencias de Rossi eran difíciles de explicar, a menos que se supusiera la presencia simultánea de dos partículas cargadas: un electrón y un positrón. En un informe previo al de Anderson, Irène Curie y Frederic Joliot también describían evidencias claras de la existencia de positrones en un experimento con una cámara de niebla y fuentes radiactivas. Sin embargo, los Joliot-Curie no supieron interpretar correctamente su resultado, pues creyeron que se trataba de un electrón casual que viajaba en sentido contrario. Aparentemente, la pareja estaba condenada a no escribir su nombre en los anales de la física de las partículas elementales, a pesar de haber tenido frente a ellos las primeras evidencias tanto del neutrón como del positrón, como ya vimos.
función vértice describe el acoplamiento entre un fotón y un electrón más allá del primer orden en teoría de perturbaciones. En particular, esta es una función irreducible de correlación de una partícula implicando el fermión  , el antifermión
, el antifermión 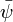 , y el potencial vectorial A.
, y el potencial vectorial A.
 , el antifermión
, el antifermión 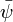 , y el potencial vectorial A.
, y el potencial vectorial A.Definición
La Función Vértice Γμ puede definirse en términos de una derivada funcional de la acción efectiva Γefec como
(En cuanto a la notación, es desafortunado que la acción efectiva Γeff y la función vértice Γμ tengan el mismo símbolo central.)
La contribución dominante (y clásica) para Γμ está en la matriz gama γμ. La función vértice está restringida por simetrías de la electrodinámica cuántica -- invariancia de Lorentz; invariancia de norma o la transversalidad del fotón, como se expresa en laidentidad de Ward; y la invariancia bajo paridad -- para tomar la siguiente forma:
donde ![\sigma^{\mu\nu} = (i/2) [\gamma^{\mu}, \gamma^{\nu}]](https://upload.wikimedia.org/math/2/5/2/252ab9beafe87bed3db823366683d0c8.png) ,
,  es el tetramomento entrante del fotón externo (en la parte derecha de la figura), y F1(q2) y F2(q2) son los factores de forma que dependen solo de la transferencia del momento q2. A nivel de árbol (o primer orden), F1(q2) = 1 y F2(q2) = 0. Más allá del primer orden, las correcciones a F1(0) se cancelan exactemente por la renormalización de la función de onda de las líneas del electrón entrante y saliente de acuerdo a la identidad de Ward-Takahashi. El factor de forma F2(0) corresponde al momento magnético anómalo a del fermión, definido en términos del factor-g de Lande como:
es el tetramomento entrante del fotón externo (en la parte derecha de la figura), y F1(q2) y F2(q2) son los factores de forma que dependen solo de la transferencia del momento q2. A nivel de árbol (o primer orden), F1(q2) = 1 y F2(q2) = 0. Más allá del primer orden, las correcciones a F1(0) se cancelan exactemente por la renormalización de la función de onda de las líneas del electrón entrante y saliente de acuerdo a la identidad de Ward-Takahashi. El factor de forma F2(0) corresponde al momento magnético anómalo a del fermión, definido en términos del factor-g de Lande como:
![\sigma^{\mu\nu} = (i/2) [\gamma^{\mu}, \gamma^{\nu}]](https://upload.wikimedia.org/math/2/5/2/252ab9beafe87bed3db823366683d0c8.png) ,
,  es el tetramomento entrante del fotón externo (en la parte derecha de la figura), y F1(q2) y F2(q2) son los factores de forma que dependen solo de la transferencia del momento q2. A nivel de árbol (o primer orden), F1(q2) = 1 y F2(q2) = 0. Más allá del primer orden, las correcciones a F1(0) se cancelan exactemente por la renormalización de la función de onda de las líneas del electrón entrante y saliente de acuerdo a la identidad de Ward-Takahashi. El factor de forma F2(0) corresponde al momento magnético anómalo a del fermión, definido en términos del factor-g de Lande como:
es el tetramomento entrante del fotón externo (en la parte derecha de la figura), y F1(q2) y F2(q2) son los factores de forma que dependen solo de la transferencia del momento q2. A nivel de árbol (o primer orden), F1(q2) = 1 y F2(q2) = 0. Más allá del primer orden, las correcciones a F1(0) se cancelan exactemente por la renormalización de la función de onda de las líneas del electrón entrante y saliente de acuerdo a la identidad de Ward-Takahashi. El factor de forma F2(0) corresponde al momento magnético anómalo a del fermión, definido en términos del factor-g de Lande como:
Método 1 de 2: Utilizar la fórmula del vértice
-
1Identifica los valores de a, b y c. En una ecuación cuadrática, el término x2 = a, el término x = b, y la constante (el término sin variable) = c. Supongamos que queremos resolver la ecuación: y = x2 + 9x + 18. En este ejemplo, a = 1, b = 9, y c = 18.
-
2Utiliza la fórmula del vértice para hallar el valor x del vértice. El vértice también determina dónde se encuentra el eje de simetría de la ecuación (x). La fórmula para hallar el valor x del vértice de una ecuación cuadrática es x = -b/2a. Introduce los valores pertinentes para calcular x. Sustituye los valores de a y de b y resuelve:
- x=-b/2a
- x=-(9)/(2)(1)
- x=-9/2
-
3Sustituye x en la ecuación original por su valor numérico para hallar el valor de y. Ahora que conoces x, solo tendrás que introducir su valor numérico en la fórmula original para hallar y. Puedes pensar en la fórmula para hallar el vértice de una función cuadrática de la siguiente forma: (x, y) = [(-b/2a), f(-b/2a)]. Esto simplemente significa que para calcular el valor de y es necesario despejar la incógnita x utilizando la fórmula, para después introducir el valor numérico hallado en la ecuación. Aquí puedes ver cómo hacerlo paso a paso:
- y = x2 + 9x + 18
- y = (-9/2)2 + 9(-9/2) +18
- y = 81/4 -81/2 + 18
- y = 81/4 -162/4 + 72/4
- y = (81 - 162 + 72)/4
- y = -9/4
-
4Escribe los valores de x y de y en forma de coordenadas. Ahora que ya sabes que x = -9/2, y y = -9/4, solo tienes que escribir estos valores en forma de coordenadas: (-9/2, -9/4). El vértice de esta ecuación cuadrática es (-9/2, -9/4). Si tuvieses que representar esta parábola en una gráfica, el vértice hallado sería el mínimo de la curva, ya que el término x2 es positivo.Anuncio
Método 2 de 2: Completar el cuadrado-
1Escribe la ecuación. Completar el cuadrado es otra forma de hallar el vértice de una ecuación cuadrática. Si empleas este método, cuando llegues al final, podrás despejar las coordenadas de x y de y, en lugar de tener que introducir el valor de x en la ecuación original. Supongamos que estamos resolviendo la siguiente ecuación cuadrática: x2 + 4x + 1 = 0'.'[1]
-
2Divide cada término entre el coeficiente del término x2. En este caso, el coeficiente de del término x2 es 1, por lo que podrás saltarte este paso. Dividir cada término entre 1 no modificaría nada.
-
3Pasa la constante a la derecha de la ecuación. La constante es el término que aparece sin coeficiente. En este caso, es 1. Pasa esta cifra la derecha de la ecuación restándolo de ambos lados del signo "=". Aquí puedes ver cómo hacerlo:[2]
- x2 + 4x + 1 = 0
- x2 + 4x + 1 -1 = 0 - 1
- x2 + 4x = - 1
-
4Completa el cuadrado al lado izquierdo de la ecuación. Para hacer esto, solo tienes que hallar (b/2)2 sumar el resultado en ambos lados de la ecuación. Sustituye b por 4, ya que 4x es el término b de esta ecuación.
- (4/2)2 = 22 = 4. Ahora, suma 4 a ambos lados de la ecuación para obtener lo siguiente:
- x2 + 4x + 4 = -1 + 4
- x2 + 4x + 4 = 3
- (4/2)2 = 22 = 4. Ahora, suma 4 a ambos lados de la ecuación para obtener lo siguiente:
-
5Factoriza el lado izquierdo de la ecuación. Como puedes comprobar, x2 + 4x + 4 es un cuadrado perfecto. Puedes expresarlo como (x + 2)2 = 3
-
6Utiliza este formato para hallar las coordenadas x e y. Puedes calcular la coordenada x igualando (x + 2)2 a cero. Entonces, si (x + 2)2 = 0, ¿cuál será el valor de x? La variable x deberá ser -2 para equilibrar el +2, por lo que la coordenada xes igual a -2. La coordenada y es el término constante que hay al otro lado de la ecuación. Por lo tanto, y es igual a 3. También puedes simplificar el proceso utilizando el número dentro del paréntesis con el signo opuesto para hallar la coordenada x. El vértice de la ecuación x2 + 4x + 1 es igual a (-2, 3).
-
-
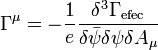


No hay comentarios:
Publicar un comentario