Efectos electromagnéticos
El efecto Hall cuántico fraccionario (EHCF) es un fenómeno físico en el que la conductancia Hall de electrones 2D muestra precisamente mesetas cuantificadas en valores fraccionarios de  . Es propiedad de un estado colectivo en que los electrones enlazan las líneas de flujo magnético con nuevas cuasipartículas, y las excitaciones tienen una carga elemental fraccionaria y posiblemente también estadística fraccional.
. Es propiedad de un estado colectivo en que los electrones enlazan las líneas de flujo magnético con nuevas cuasipartículas, y las excitaciones tienen una carga elemental fraccionaria y posiblemente también estadística fraccional.
 . Es propiedad de un estado colectivo en que los electrones enlazan las líneas de flujo magnético con nuevas cuasipartículas, y las excitaciones tienen una carga elemental fraccionaria y posiblemente también estadística fraccional.
. Es propiedad de un estado colectivo en que los electrones enlazan las líneas de flujo magnético con nuevas cuasipartículas, y las excitaciones tienen una carga elemental fraccionaria y posiblemente también estadística fraccional.
El EHCF fue descubierto experimentalmente en 1982 por Daniel C. Tsui y Horst Störmer, en experimentos realizados en heteroestructuras de arseniuro de galiodesarrolladas por Arthur Stone Gossard. Robert B. Laughlin, Tsui y Störmer fueron galardonados con el Premio Nobel de física de 1998 por el descubrimiento y la explicación del EHCF.
Introducción
El EHCF es un comportamiento colectivo en algún sistema bidimensional de electrones. En campos magnéticos particulares, el gas de electrones se condensa en un notable estado líquido, que es muy delicado, pues requiere de material de alta calidad con una concentración baja de portadores de carga y las temperaturas extremadamente bajas. Como en el efecto Hall cuántico entero, una serie de mesetas forman la resistencia de Hall. Cada valor particular del campo magnético corresponde a un factor de relleno (la proporción de electrones a cuantos de flujo magnético):
donde p y q son números enteros sin factores comunes. Aquí q resulta para ser un número impar, con la excepción de dos factores de llenado 5/2 y 7/2. Las series principales de esas fracciones son:
y
Se dieron varios pasos importantes en la teoría EHCF.
- Estados de Laughlin y cuasipartículas cargadas fraccionariamente: esta teoría, propuesta por Laughlin, se basa en funciones de onda prueba exactas para el estado base en la fracción
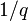 así como en sus excitaciones cuasipartícula y cuasiagujero. Las excitaciones tienen carga fraccionaria de magnitud
así como en sus excitaciones cuasipartícula y cuasiagujero. Las excitaciones tienen carga fraccionaria de magnitud 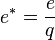 .
.
- Estadísticas de intercambio fraccional de cuasipartículas: Bertrand Halperin conjeturó y Daniel Arovas, J. R. Schrieffer y Frank Wilczek demostraron, que las excitaciones de cuasipartículas cargadas fraccionariamente de los estados de Laughlin son axiones con ángulo de estadística fraccionaria
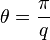 ; la función de onda adquiere el factor de fase
; la función de onda adquiere el factor de fase 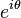 (junto con un factor de fase de Aharonov-Bohm) cuando se intercambian cuasipartículas idénticas en un sentido antihorario. Un experimento reciente parece dar una clara demostración de este efecto.2
(junto con un factor de fase de Aharonov-Bohm) cuando se intercambian cuasipartículas idénticas en un sentido antihorario. Un experimento reciente parece dar una clara demostración de este efecto.2
- Estados de jerarquía: esta teoría fue propuesta por Duncan Haldane y aclarada más tarde por Halperin, para explicar las fracciones de relleno observados no producidas en los estados de Laughlin
 . A partir de los estados de Laughlin, nuevos estados en diferentes rellenos pueden estar formados por condensación de cuasipartículas en sus propios estados de Laughlin. Los nuevos estados y sus rellenos están limitados por las estadísticas fraccionarias de las cuasipartículas, produciendo por ejemplo,
. A partir de los estados de Laughlin, nuevos estados en diferentes rellenos pueden estar formados por condensación de cuasipartículas en sus propios estados de Laughlin. Los nuevos estados y sus rellenos están limitados por las estadísticas fraccionarias de las cuasipartículas, produciendo por ejemplo,  y
y  del estado de Laughlin
del estado de Laughlin 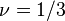 . Asimismo la construcción de otra serie de nuevos estados por condensación de cuasipartículas de la primera serie de nuevos estados y así sucesivamente, produce una jerarquía de estados que abarcan todas las fracciones de relleno de denominador impar. Esta idea ha sido validada cuantitativamente,3 y saca las fracciones observadas en un orden natural. El modelo de plasma original de Laughlin se extendió a los estados de jerarquía por MacDonald y otros.4
. Asimismo la construcción de otra serie de nuevos estados por condensación de cuasipartículas de la primera serie de nuevos estados y así sucesivamente, produce una jerarquía de estados que abarcan todas las fracciones de relleno de denominador impar. Esta idea ha sido validada cuantitativamente,3 y saca las fracciones observadas en un orden natural. El modelo de plasma original de Laughlin se extendió a los estados de jerarquía por MacDonald y otros.4
- Fermiones compuestos: esta teoría fue propuesta por Jain y ampliada por Halperin, Lee y Read. La idea básica de esta teoría es que como resultado de las interacciones repulsivas, dos (o, en general, un número incluso de) vórtices son capturados por cada electrón, formando cuasipartículas cargadas enteras llamadas fermiones compuestos. Los estados fraccionales de los electrones se entienden como el entero EHC de fermiones compuestos. Por ejemplo, esto hace que los electrones en factores de relleno 1/3, 2/5, 3/7, etc. se comporten de la misma manera que en el factor de relleno 1, 2, 3, etc. Se han observado fermiones compuestos, y la teoría ha sido parcialmente verificada por experimentos y cálculos de ordenador. Los compuestos de fermiones son válidos más allá del efecto Hall; cuántico por ejemplo, el factor de relleno 1/2 corresponde a cero campo magnético para fermiones compuestos, resultando en su mar de Fermi. La teoría de fermión compuesto proporciona una descripción complementaria de los estados de Laughlin y de jerarquía. Esto da pruebas que las funciones de onda, aunque no idénticas a las producidas desde la imagen de la jerarquía (las funciones de onda para los estados de Laughlin son idénticas), están en la misma clase de universalidad, como se muestra por Read. No existen pruebas experimentales para estados Hall cuánticos que, incluso en principio, permiten confirmar la descripción de fermión compuesto, con exclusión de la descripción de la jerarquía.
El EHCF fue descubierto experimentalmente en 1982 por Daniel C. Tsui y Horst Störmer, en experimentos realizados en heteroestructuras de arseniuro de galiodesarrolladas por Arthur Stone Gossard. Laughlin, Tsui y Störmer fueron galardonados con el Premio Nobel de 1998 por su trabajo.
Las cuasipartículas cargadas fraccionariamente no son ni bosones ni fermiones, y exhiben estadísticas axiónicas. El efecto Hall cuántico sigue siendo influyente en las teorías sobre el orden topológico. Ciertas fases de Hall cuántico parecen tener las propiedades adecuadas para construir un ordenador cuántico topológico.
Evidencia de cuasipartículas cargadas fraccionariamente
Los Experimentos han dado resultados que apoyan específicamente el entendimiento que sí hay cuasipartículas cargadas fraccionalmente en un gas de electrones en condiciones EHCF.
En 1995, se midió la carga fraccional de cuasipartículas Laughlin directamente en un electrómetro antipunto cuántico en la Universidad de Stony Brook, Nueva York.5En 1997, dos grupos de físicos del Instituto Weizmann de Ciencias en Rejovot, Israel y en el laboratorio Commissariat à l'énergie atomique cerca de París, detecta estas cuasipartículas que llevan una corriente eléctrica, a través de la medición ruido de disparo cuántico.6 7 Estos experimentos son algo controvertidos.
Un experimento más reciente (2004),8 que mide la carga de cuasipartícula muy directamente, aparece irreprochable.
Impacto de efecto Hall cuántico fraccionario
El EHCF muestra los límites de la teoría de simetría rota de Landau. Previamente, durante mucho tiempo, se creyó que la teoría de simetría rota, podría explicar todos los conceptos importantes y propiedades esenciales de todas las formas de la materia. Según este punto de vista, lo único que hacer es aplicar la teoría de simetría rota, a todos los diferentes tipos de fases y transiciones de fase. Desde esta perspectiva, podemos entender la importancia del EHCF descubierto por Tsui, Stormer y Stone Gossard.
Diferentes estados HCF tienen la misma simetría y no pueden ser descrito por la teoría de simetría rota. Por lo tanto los estados HCF representan nuevos estados de la materia que contienen un nuevo tipo de orden: orden topológico. La existencia de líquidos HCF indica que existe todo un mundo nuevo, más allá del paradigma de la simetría rota, que espera ser explorado. El efecto HCF abrió un nuevo capítulo en la física de materia condensada. El nuevo tipo de órdenes representado por estados HCF enriquecen enormemente nuestro comprensión de las fases de cuanto y de las transiciones de fase cuántica. La carga fraccionada asociada, estadísticas fraccionales, estadísticas no abelianas, estados de borde quiral, etc. demuestran el poder y la fascinación de emergencia en sistemas de muchos cuerpos.
El efecto Hall cuántico se observa en materiales a muy baja temperatura. Sin embargo, en el grafeno dicho efecto también se observa a temperatura ambiente (descubierto en 2005) siendo el responsable de sus propiedades como semiconductor y dando lugar a las aplicaciones electrónicas del grafeno. Más aún, los niveles de Landau están indexados por un número entero, pero en ciertos materiales se observa que aparecen niveles indexados por un número no entero, se trata del efecto Hall cuántico fraccionario. En estos materiales la unidad de carga más pequeña no es el electrón, sino una fracción del electrón. Se ha observado que los electrones en el material se rompen en trozos, unas cuasipartículas de carga fraccionaria. Estas cuasipartículas exóticas tienen propiedades cuánticas muy curiosas que han sido demostradas experimentalmente. El material ideal para observar dichas propiedades y utilizarlas en aplicaciones es el grafeno.
El descubrimiento de que en el grafeno también se puede observar el efecto Hall cuántico fraccionario a temperaturas altas (aunque todavía no a temperatura ambiente, ya que se ha podido observar sólo a 20 K), es un gran avance (es una temperatura 100 veces superior a la de otros materiales). El dispositivo utilizado requiere suspender una tira de grafeno de unas pocas micras entre dos contactos de forma que los efectos del substrato no impidan observar el efecto Hall cuántico fraccionario. El resultado ha sido la observación de cuasipartículas con una carga de 1/3 la carga del electrón. Ahora los investigadores tendrán que caracterizar las funciones de onda de estas cuasipartículas y comprobar si corresponden a lo predicho para la teoría en función de la ecuación de Dirac para los electrones. Una posibilidad es aprovechar que el grafeno es plano para utilizar el microscopio de efecto túnel y visualizar dichas funciones de onda de carga fraccionaria directamente.
Por ahora las aplicaciones de este descubrimiento se limitarán al campo teórico, donde muchas cosas quedan aún por corroborar y descubrir en este interesante campo científico. Las aplicaciones prácticas que podrán tener estos descubrimientos son ahora difíciles de imaginar, pero haberlas las habrá.
efecto Joule al fenómeno irreversible por el cual si en un conductor circula corriente eléctrica, parte de la energía cinética de los electrones se transforma en calor1 2 debido a los choques que sufren con los átomos del material conductor por el que circulan, elevando la temperatura del mismo. El nombre es en honor a su descubridor, el físico británico James Prescott Joule.
El movimiento de los electrones en un cable es desordenado, esto provoca continuas colisiones con los núcleos atómicos y como consecuencia una pérdida de energía cinética y un aumento de la temperatura en el propio cable.
Efecto Joule
Este efecto es utilizado para calcular la energía disipada en un conductor atravesado por una corriente eléctrica de la siguiente manera:
La potencia P disipada en un conductor es igual a la diferencia de potencial V a la que está sometido multiplicada por la intensidad de corriente I que lo atraviesa. La energía desarrollada E es el producto de la potencia P por el tiempo t transcurrido, luego la energía E es el producto de la tensión V por la intensidad I y por el tiempo t.
Si a esta expresión añadimos la Ley de Ohm tendremos:
La energía desarrollada es igual al cuadrado de la intensidad por la resistencia y por el tiempo, o lo que es lo mismo, el cuadrado de la tensión dividido por la resistencia y por el tiempo.
Microscópicamente el efecto Joule se calcula a través de la integral de volumen del campo eléctrico  por la densidad de corriente
por la densidad de corriente 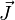 :
:
 por la densidad de corriente
por la densidad de corriente 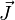 :
:
La resistencia es el componente que transforma la energía eléctrica en calor, (por ejemplo un hornillo eléctrico, una estufa eléctrica, una plancha etc.).
Qué es el efecto Joule y por qué ocurre
El efecto Joule, a vista de pájaro, esel desprendimiento de calor provocado por el movimiento de electrones –también conocido como corriente eléctrica– por un material. Este efecto se recoge en la fórmula Q = P x t, donde “Q” es energía o calor desprendido (también representada por la letra E y medida en Julios o Calorías), “P” la potencia consumida (medida en vatios) y “t” el tiempo transcurrido (medido en segundos).
Para entender el efecto Joule,debemos entender el origen de las corrientes eléctricas. Para ello, imaginemos un circuito simple con una pila de 6 Voltios (con un polo positivo y otro negativo) y una resistencia de unos 3 ohmios.
- Al conectar la pila al circuito, los electrones almacenados en la pila comenzarán a recorrer el circuito desde el polo positivo hasta el negativo, atravesando los cables y la resistencia conectada al mismo.
- Estos electrones se mueven a causa de una diferencia de potencial –que, en este caso, es de 6 voltios–. Para entender dicho concepto, imaginemos una escalera. El polo positivo es la zona superior de la escalera. El polo negativo, la zona inferior. Desde la zona superior, hacemos rodar unas bolas. Estas, inevitablemente, comenzarán a descender hacia abajo por la fuerza gravitatoria. Con los electrones ocurre algo similar. Este movimiento de electrones del polo positivo (mayor potencial) al polo negativo (menor potencial) es lo que conocemos como corriente eléctrica.
- Al moverse esos electrones, estos impactan con otros átomos y partículas subatómicas (las que componen los cables, las resistencias, etc.) y, por lo tanto, provocan que estas se muevan en mayor o menor medida. Al aumentar su movimiento, aumenta su energía y, por lo tanto, el desprendimiento de calor al exterior. Este desprendimiento inevitable –solo sería evitable si los materiales conductores fueran 100% perfectos, algo que es imposible de lograr– de energía en forma de calor se conoce como el efecto Joule.
Los calefactores son un claro ejemplo de aplicación del efecto Joule.
El efecto Joule y la cantidad de calor que se desprende depende de varias variables:
- La intensidad de corriente. O el número de electrones que pasan por unidad de tiempo. Para entender este concepto, imaginemos una tubería de agua. Cuanto mayor diámetro tenga la tubería de agua, más caudal podrá atravesarla en una unidad de tiempo. La intensidad de corriente es similar. Cuanto menor sea la resistencia y mayor sea la diferencia de potencial, mayor será será la cantidad de electrones en movimiento en una unidad de tiempo.
- La resistencia. Es la oposición que presenta un elemento al paso de los electrones por el mismo. Normalmente entendemos como resistencia a un elemento concreto (que puede ser una bombilla o cualquier otro), pero la resistencia también está presente en los cables, por ejemplo. Y es que todo material por el que pasa la corriente eléctrica, presenta oposición al paso de electrones. Si no la presentaran, se obtendría el mayor rendimiento posible de todos los sistemas y el calor generado sería ínfimo. Para que podamos comprender mejor este concepto: la resistencia podríamos entenderla como el número de obstáculos que tendría que sortear un atleta en una carrera de 200 metros obstáculos. Cuanto mayor sea la resistencia, mayor será el número de obstáculos que se presenten en el camino del electrón.
- La diferencia de potencial o voltaje. Volviendo a la analogía, la diferencia de potencial la podríamos entender como la diferencia de altura existente entre la parte superior de una escalera y la parte inferior. En dicho ejemplo, la gravedad atrae a los cuerpos de la zona superior. En el caso de la corriente eléctrica, los átomos son los que atraen los electrones del polo positivo al negativo, generando ese movimiento.
- Tiempo. Cuanto mayor es el tiempo, la cantidad de calor generada aumenta. Por lo tanto también influye.
- Potencia. Normalmente, la influencia de la resistencia, la intensidad y la diferencia de potencial de un circuito se reúne en una magnitud conocida como potencia (que es la que aparece en la fórmula anterior).
El efecto Joule, algo deseado y despreciado
A priori, el efecto Joule puede parecer algo totalmente despreciable, puesimpide la obtención de la máxima cantidad de energía de una corriente eléctrica que alimenta a un sistema. Por ejemplo, en los procesadores es algo que siempre se trata de evitar, pues se trata aprovechar la mayor cantidad de energía eléctrica para aumentar el rendimiento del ordenador, tablet o smartphone al que está conectado.
El efecto Joule es un efecto alabado y, al mismo tiempo, despreciadoPero el efecto Joule también es algo muy deseado y esencial para muchos productos actuales. Productos como las estufas, los calefactores, los termos, los secadores o incluso las vitrocerámicas. Y es que este efecto permite convertir la energía eléctrica en calor, algo que ha sido muy explotado por ingenieros durante el último siglo para la creación de un sinfín de productos.
En el caso de los secadores, por ejemplo, encontramos una serie de resistencias que se calientan con el paso de la corriente eléctrica, calentando así el aire que expulsa al exterior. El juego está en tratar de obtener la mayor eficiencia energética (con la menor cantidad de electricidad posible, calentar el aire a una misma temperatura).
Así pues, el efecto Joule es, como todo en esta vida, algo muy relativo. Dependiendo del ámbito y la situación en la que nos encontremos, nos interesará su aparición o no. Pero eso es algo con lo que tendremos que lidiar mientras la energía eléctrica sea una de las bases de nuestra sociedad.




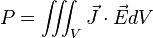
No hay comentarios:
Publicar un comentario