Electrodinámica
Los campos electromagnéticos se propagan por el espacio en forma de ondas, que pueden viajar a través de un medio así como en el vacío. Las ecuaciones de onda electromagnéticas son necesarias para describir la propagación de las ondas electromagnéticas, tanto en presencia de materia como en el vacío.
Ecuaciones de onda y las ecuaciones de Maxwell
Como se puede apreciar tenemos ecuaciones de onda tanto para el campo eléctrico  como para el campo magnético
como para el campo magnético  , que son obtenidas a partir de las ecuaciones de Maxwell teniendo que:
, que son obtenidas a partir de las ecuaciones de Maxwell teniendo que:
 como para el campo magnético
como para el campo magnético  , que son obtenidas a partir de las ecuaciones de Maxwell teniendo que:
, que son obtenidas a partir de las ecuaciones de Maxwell teniendo que:

Para obtener las ecuaciones es necesario aplicar el operador rotacional a ambas.
Ecuación de onda para E
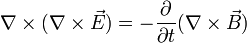
Sustituyendo 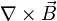 y aplicando identidad de rotacional tenemos:
y aplicando identidad de rotacional tenemos:
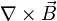 y aplicando identidad de rotacional tenemos:
y aplicando identidad de rotacional tenemos: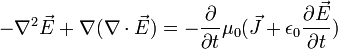
Ahora bien, sabemos que la segunda parte del lado izquierdo es cero y 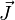 es cero en el vacío, quedándonos solo
es cero en el vacío, quedándonos solo
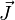 es cero en el vacío, quedándonos solo
es cero en el vacío, quedándonos solo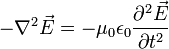
Ahora, igualando a cero y sabiendo que  , siendo c la velocidad de la luz, tenemos la ecuación de onda para
, siendo c la velocidad de la luz, tenemos la ecuación de onda para  :
:
 , siendo c la velocidad de la luz, tenemos la ecuación de onda para
, siendo c la velocidad de la luz, tenemos la ecuación de onda para  :
:
Ecuación de onda para B
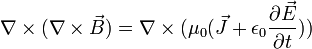
Aplicando las mismas identidades que con  y sabiendo que
y sabiendo que 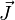 , también es cero, nos queda:
, también es cero, nos queda:
 y sabiendo que
y sabiendo que 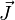 , también es cero, nos queda:
, también es cero, nos queda:
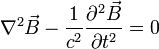
efecto Nernst (también conocido como primer efecto Nernst–Ettingshausen, en honor de Walther Nernst y Albert von EttingshausenNota 1 ) es un fenómeno termoeléctrico (o termomagnético) observado cuando una muestra que permite la conducción eléctrica se somete a un campo magnético y a un gradiente de temperatura normal al campo. En estas circunstancias, se inducirá un campo eléctrico normal a ambos.
Este efecto se mide a través del coeficiente de Nernst |N|, que se define como
donde Ey es la componente y del campo eléctrico que resulta de la componente z del campo magnético Bz y del gradiente de temperatura dT/dx.
El proceso inverso se conoce como efecto Ettingshausen o como segundo efecto Nernst-Ettingshausen.
Imagen física
Los portadores de energía móviles (por ejemplo, los electrones en la banda de conducción en un semiconductor) se moverán a lo largo de los gradientes de temperatura debido a la estadística y a la relación entre temperatura y energía cinética. Si existe un campo magnético transversal al gradiente de temperatura y los portadores estáncargados eléctricamente, estos experimentarán una fuerza perpendicular a la dirección del movimiento (que es la misma que la dirección del gradiente de temperatura) y al campo magnético. Por esta razón se inducirá un campo eléctrico.
Ejemplos
Los semiconductores presentan el efecto Nernst. Esto ha sido estudiado en los años 1950 por Krylova, Mochan y muchos otros. Sin embargo, en los metales, este fenómeno es prácticamente inexistente. El efecto aparece en la fase vortical de semiconductores tipo II debido al movimiento de los vórtices; esto ha sido estudiado por Huebener et al. Los superconductores a altas temperaturas presentan el efecto Nernst tanto en la fase superconductiva como en la fase de pseudobandas, de acuerdo a Xu et al. Los superconductores de fermiones pesados pueden presentar una fuerte señal del efecto Nernst, la cual posiblemente no se debe a los vórtices, como mostraron Bel et al.
escalera de Jacob, llamada en inglés Jacob's ladder, al arco eléctrico producido por un dispositivo formado por dos conductores rectos en forma de V.
El arco se produce en la parte más cercana (baja) de los electrodos y a medida que el aire superior es ionizado por la radiación ultravioleta y por el calor, va subiendo hasta que la distancia de los electrodos es demasiado larga y desaparece, repitiéndose el arco en la parte más estrecha y así sucesivamente.
Para que se produzca el arco se necesita normalmente una diferencia de tensión entre electrodos mayor de 5.000 voltios.
Para mejorar el cebado del arco y que este se inicie en la parte más baja de la V, se introduce un tercer electrodo corto (llamado de Gabriel) entre los dos principales. Va conectado a uno de los electrodos principales por una resistencia.
Este dispositivo se utilizaba mucho en las películas de ciencia ficción antiguas.
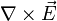 e igualando a cero, tenemos la
e igualando a cero, tenemos la 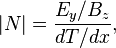
No hay comentarios:
Publicar un comentario