Electrodinámica
El operador D'Alembertiano es la generalización del operador laplaciano a un espacio de Minkowski, o, más en general, a un espacio de dimensión y métrica arbitraria. Se suele representar como 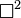 , o simplemente como
, o simplemente como  . Técnicamente el D'Alembertiano de una función escalar es el operador de Laplace-Beltrami asociado a la métrica de dicho espacio, operando sobre dicha función.
. Técnicamente el D'Alembertiano de una función escalar es el operador de Laplace-Beltrami asociado a la métrica de dicho espacio, operando sobre dicha función.
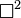 , o simplemente como
, o simplemente como  . Técnicamente el D'Alembertiano de una función escalar es el operador de Laplace-Beltrami asociado a la métrica de dicho espacio, operando sobre dicha función.
. Técnicamente el D'Alembertiano de una función escalar es el operador de Laplace-Beltrami asociado a la métrica de dicho espacio, operando sobre dicha función.
Su definición es, por analogía con el operador nabla ordinario de  , el producto escalar del vector de derivadas parciales consigo mismo. En una variedad (pseudo)riemanniana el operador nabla se define como:
, el producto escalar del vector de derivadas parciales consigo mismo. En una variedad (pseudo)riemanniana el operador nabla se define como:
 , el producto escalar del vector de derivadas parciales consigo mismo. En una variedad (pseudo)riemanniana el operador nabla se define como:
, el producto escalar del vector de derivadas parciales consigo mismo. En una variedad (pseudo)riemanniana el operador nabla se define como:
Esta forma manifiestamente covariante implica la invarianza de este operador frente a transformaciones de Lorentz; y representa la ecuación de onda electromagnética.
En el espacio de Minkowski
La métrica es la métrica plana  , y por tanto el D'Alambertiano es
, y por tanto el D'Alambertiano es
 , y por tanto el D'Alambertiano es
, y por tanto el D'Alambertiano esEn un espacio curvo
Se puede hacer que el operador D'Alembertiano sea también invariante frente a una transformación general de coordenadas si se define en relación a la derivada covariante:
Ejemplos
Un ejemplo de utilización del D'Alambertiano sería la ecuación de Klein-Gordon, que describe campos escalares de spin cero:
Las ecuaciones de Jefimenko, en recuerdo de Oleg D. Jefimenko (Yefimenko), describen el comportamiento de los campos eléctrico y magnético en función de la posición de las fuentes del campo en instantes retardados. Junto con la ecuación de continuidad, las ecuaciones de Jefimenko () son equivalentes a las ecuaciones de Maxwell.
Campo electromagnético en el vacío
El campo eléctrico  y el campo magnético
y el campo magnético  vienen dados en términos de la densidad de carga
vienen dados en términos de la densidad de carga  y la densidad de corriente
y la densidad de corriente 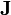 como:
como:
 y el campo magnético
y el campo magnético  vienen dados en términos de la densidad de carga
vienen dados en términos de la densidad de carga  y la densidad de corriente
y la densidad de corriente 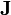 como:
como:(1)
Donde  , y
, y  . El uso del tiempo retardado, tr, signifca que el campo en el instante t a una distancia R de las cargas depende de como estaban las cargas situadas en un instante anterior, debido a la velocidad de propagación finita del campo, la cual se corresponde con la velocidad de la luz en el vacío. EL campo que medimos en un lugar e instante dados viene creado por la fuente del campo en un tiempo anterior, llamado tiempo retardado. Este tiempo depende de la distancia entre el punto de observación y la fuente en el instante en que esta originó el campo.
. El uso del tiempo retardado, tr, signifca que el campo en el instante t a una distancia R de las cargas depende de como estaban las cargas situadas en un instante anterior, debido a la velocidad de propagación finita del campo, la cual se corresponde con la velocidad de la luz en el vacío. EL campo que medimos en un lugar e instante dados viene creado por la fuente del campo en un tiempo anterior, llamado tiempo retardado. Este tiempo depende de la distancia entre el punto de observación y la fuente en el instante en que esta originó el campo.
 , y
, y  . El uso del tiempo retardado, tr, signifca que el campo en el instante t a una distancia R de las cargas depende de como estaban las cargas situadas en un instante anterior, debido a la velocidad de propagación finita del campo, la cual se corresponde con la velocidad de la luz en el vacío. EL campo que medimos en un lugar e instante dados viene creado por la fuente del campo en un tiempo anterior, llamado tiempo retardado. Este tiempo depende de la distancia entre el punto de observación y la fuente en el instante en que esta originó el campo.
. El uso del tiempo retardado, tr, signifca que el campo en el instante t a una distancia R de las cargas depende de como estaban las cargas situadas en un instante anterior, debido a la velocidad de propagación finita del campo, la cual se corresponde con la velocidad de la luz en el vacío. EL campo que medimos en un lugar e instante dados viene creado por la fuente del campo en un tiempo anterior, llamado tiempo retardado. Este tiempo depende de la distancia entre el punto de observación y la fuente en el instante en que esta originó el campo.Campo magnético en presencia de medios dieléctricos y diamagnéticos
Las dos expresiones anteriores para el campo eléctrico y magnético admiten extensiones al caso de campos electromagnéticos en medios dieléctricos arbitrarios.1
Los campos macroscópicos  ,
, 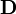 ,
,  y
y  se expresan entonces en términos de la densidad de carga
se expresan entonces en términos de la densidad de carga  , la densidad de corriente
, la densidad de corriente 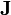 , la polarización
, la polarización  , y lamagnetización
, y lamagnetización 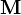 .
.
La ecuación de Clausius-Mossoti lleva el nombre del físico italiano Octavio Fabricio Mossotti, cuyo libro de 18501 analizó la relación entre las constantes dieléctricasde dos medios diferentes, y el físico alemán Rudolf Clausius, quien dio la fórmula de forma explícita en su libro de 18792 en el contexto no de constantes dieléctricas, sino de los índices de refracción.
La ley de Clausius-Mossotti se aplica a la constante dieléctrica de un dieléctrico que es perfecto, homogéneo e isotrópico:3
donde
 es la constante dieléctrica de una sustancia
es la constante dieléctrica de una sustancia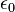 es la permitividad del vacío
es la permitividad del vacío es la masa molar de la sustancia
es la masa molar de la sustancia es su densidad
es su densidad es el número de Avogadro, y
es el número de Avogadro, y es la polarizabilidad molecular.
es la polarizabilidad molecular.
Ecuación
La ecuación relaciona la permitividad del medio  en términos de las propiedades moleculares, por tanto, asumiendo la expresión aproximada para el campo total en un medio dieléctrico:
en términos de las propiedades moleculares, por tanto, asumiendo la expresión aproximada para el campo total en un medio dieléctrico:
 en términos de las propiedades moleculares, por tanto, asumiendo la expresión aproximada para el campo total en un medio dieléctrico:
en términos de las propiedades moleculares, por tanto, asumiendo la expresión aproximada para el campo total en un medio dieléctrico:
donde  es el vector polarización eléctrica como se conoce usualmente.
es el vector polarización eléctrica como se conoce usualmente.
 es el vector polarización eléctrica como se conoce usualmente.
es el vector polarización eléctrica como se conoce usualmente.
El factor que acompaña a  puede diferir de
puede diferir de  aunque se ha asumido que es el orden correcto de magnitud. Para dieléctricos lineales,
aunque se ha asumido que es el orden correcto de magnitud. Para dieléctricos lineales,
 puede diferir de
puede diferir de  aunque se ha asumido que es el orden correcto de magnitud. Para dieléctricos lineales,
aunque se ha asumido que es el orden correcto de magnitud. Para dieléctricos lineales,
Donde  es el número de moléculas por unidad de volumen y
es el número de moléculas por unidad de volumen y  es la polarizabilidad molecular.
es la polarizabilidad molecular.
 es el número de moléculas por unidad de volumen y
es el número de moléculas por unidad de volumen y  es la polarizabilidad molecular.
es la polarizabilidad molecular.
Puesto que 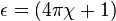 , sustituyendo en la ecuación anterior:
, sustituyendo en la ecuación anterior:
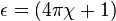 , sustituyendo en la ecuación anterior:
, sustituyendo en la ecuación anterior:
Dado que esta expresión fue derivada originalmente para valores con bajos valores de N, se cumple para materiales no polares más densos.
Factor de Clausius-Mossotti
donde:
 es la permitividad (el subíndice p se refiere a una esfera dieléctrica sin pérdidas en suspensión en un medio m)
es la permitividad (el subíndice p se refiere a una esfera dieléctrica sin pérdidas en suspensión en un medio m) es la conductividad
es la conductividad es la frecuencia angular de la aplicación del campo eléctrico
es la frecuencia angular de la aplicación del campo eléctrico es la unidad imaginaria, la raíz cuadrada de -1
es la unidad imaginaria, la raíz cuadrada de -1
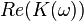 se puede medir directamente por la aplicación de diferentes potenciales de CA directamente en los electrodos,,7
se puede medir directamente por la aplicación de diferentes potenciales de CA directamente en los electrodos,,7  se puede medir por electro-rotación gracias a los métodos de captura de las mediciones ópticas.
se puede medir por electro-rotación gracias a los métodos de captura de las mediciones ópticas.ECUACION DE CLAUSIUS-MOSOTTI
A partir de las expresiones reflejadas anteriormente para la polarización en el medio y para el campo local podemos escribir :
de donde :
Por otra parte la polarización resulta ser en la mayor parte de los medios proporcional al campo aplicado :
siendo e la denominada permitividad dieléctrica del medio. Combinando ambas expresiones obtenemos :
expresión que nos proporciona la permitividad y recibe el nombre de ecuación de Clausius-Mosotti. Esta ecuación puede reescribir también de la forma más usual en la bibliogarfía:
Volviendo a considerar la primera forma de esta ecuación y escribiendo explícitamente la polarizabilidad :
Esta expresión diverge cuando el denominador se hace nulo, es decir en la situación en que Na /3e o = 1. Dado que la polarizabilidad depende de la temperatura, existirá siempre un valor de la misma para la cual se verifique esta condición. Por tanto, de acuerdo con este modelo todos los materiales polares deberían presentar polarización espontánea (polarización sin campo aplicado) a una cierta temperatura. Este hecho no corresponde a la realidad y suele denominarse catástrofe de Mosotti.
Para la mayoría de los materiales Na /3e o << 1 y aparece el comportamiento dieléctrico ordinario. Sin embargo en algunos sólidos se verifica la condición de catástrofe dando origen a polarización espontánea. Estos materiales se denominan ferroeléctricos y son equivalentes a los imanes en magnetismo. Un caso típico es el BaTiO3 que muestra polarización espontánea por debajo de 120 ºC.
En los materiales ferroeléctricos tendremos pues una disposición ordenada de sus dipolos elementales incluso sin campo aplicado. Estos dipolos tienden espontáneamente a orientarse paralelos entre sí. Sin embargo la influencia de otros factores hace que una muestra de tamaño finito de un material de este tipo muestre una disposición no uniforme de polarización. De hecho tiende a presentar zonas de polarización uniforme pero cuya dirección sentido cambia de una región a otra.




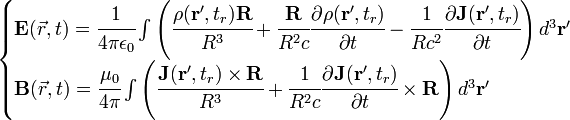
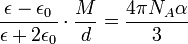




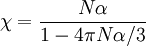


No hay comentarios:
Publicar un comentario