Álgebra de Clifford
Las álgebras de Clifford son álgebras asociativas de importancia en matemáticas, en particular en teoría de la forma cuadrática y del grupo ortogonal y en la física. Se nombran así por William Kingdon Clifford.
Definición formal
Sea V un espacio vectorial sobre un cuerpo k y q : V → k una forma cuadrática en V. El álgebra de Clifford C(q) es un álgebra asociativa unital sobre k junto con lafunción lineal i: V → C(q) definido por la propiedad universal siguiente: para cada álgebra asociativa A sobre k con una función lineal j: V → A tal que para cada v en Vse tiene j(v)² = q(v)1 (donde 1 denota la identidad multiplicativa de A), hay un homomorfismo único del álgebra f: C(q) → A tal que el diagrama siguiente conmuta
es decir tal que fi = j.
El álgebra de Clifford existe y puede ser construida como sigue: tome el álgebra tensorial T(V) construida por el ideal generado por
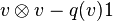 .
.
Se sigue de esta construcción que i es inyectivo, y V se puede considerar como subespacio lineal de C(q).
Sea
- B(u, v) = q(u + v) - q(u) - q(v)
la forma bilineal asociada a q. Que es una consecuencia de la definición que la identidad
- uv + vu = B (u, v)
vale en C(q) para cada par (u, v) de vectores en V. Si el cuerpo es de característica distinta de 2 esta expresión se puede utilizar como definición alternativa.
El álgebra de Clifford C(q) es filtrada por subespacios
- k ⊂ k + V ⊂ k + V + V² ⊂ ...
de los elementos que se pueden escribir como monomios de 0, 1, 2,.. vectores en V. El álgebra graduada asociada es canónicamente isomorfa al álgebra exterior Λ V del espacio vectorial. Esto muestra en particular que
- dim C(q) = 2dim V.
Una manera más simple de considerar esto es eligiendo una base arbitraria e1, e2..... para V. Usando la relación de anticonmutación podemos expresar siempre un elemento del álgebra de Clifford como combinación lineal de monomios del tipo
que da un isomorfismo explícito con el álgebra exterior. Obsérvese que éste es un isomorfismo de espacios vectoriales, no de álgebras.
Si V tiene dimensión finita par, el cuerpo es algebraicamente cerrado y la forma cuadrática es no degenerada, el álgebra de Clifford es simple central. Así por el teorema de Artin-Wedderburn es (no canónicamente) isomorfa a un álgebra de matrices. Se sigue que en este caso C(q) tiene una representación irreducible de dimensión 2dim(V)/2 que es única salvo un isomorfismo (no único). Éste es la famosa representación por espinor), y sus vectores se llaman espinores.
En caso de que el cuerpo k sea el cuerpo de números reales el álgebra de Clifford de una forma cuadrática de signatura p, q es generalmente denotada C(p, q). Se han clasificado estas álgebras reales de Clifford como sigue...
Las álgebras de Clifford son importantes en la física. Los físicos consideran generalmente las álgebras de Clifford expresadas por las matrices γ1...,γn que tienen la propiedad que
- γi γj + γj γi = 2δi,j
donde δ es la matriz de una forma cuadrática del tipo p,q con respecto a una base ortonormal de e1,..., en.
Representaciones matriciales de las álgebras reales de Clifford
Tendremos que estudiar matrices anticomutantes (AB = -BA) porque en las álgebras de Clifford los vectores ortogonales anticonmutan
Para las álgebras de Clifford reales Rp,q se necesitan p + q matrices mutuamente anticonmutantes, de las cuales p tienen +1 como cuadrado y q tienen −1 como cuadrado.
El sistema "K" para nombrar matrices
Primero presentamos un método cómodo para nombrar matrices 2n x 2n
Note que K0 es la matriz identidad. Los nombres fueron elegidos de tal manera que hay una regla simple para recordar los productos:
- K1 K2 = K3
- K1 K3 = K2
- K2 K3 = K1
- K2 K1 = -K3
- K3 K1 = -K2
- K3 K2 = -K1.
El incremento de índices da resultado positivo. Índices que disminuyen da resultado negativo.
¡Atención! Éstas no son las mismas relaciones que valen para la base estándar de los cuaterniones. Si se nombrara i = i1, j = i2 y k = i3 se conseguiría
- i1 i2 = i3
- i2 i3 = i1
- i3 i1 = i2
la última regla es diferente. Veremos más adelante que los quaterniones puros i,j y k se pueden representar por K12, K20 y K32
Se recalca que
K2 es la única con el cuadrado negativo, así que puede ser vista como la representación más simple de i.
Entonces damos a todos los posibles productos de Kronecker un nombre (véase multiplicación de matrices):
Algunos ejemplos
Cada índice tiene su nivel (2x2, 4x4, 8x8, 16x16...)
K13 es una K3 en el nivel 2x2 y una K1 en el nivel 4x4. Con esta notación es muy fácil multiplicar matrices cuadradas grandes pusto que
Resolvamos un ejemplo
- K123 K222 = K301
- nivel-8x8 1 por 2 da 3
- nivel-4x4 2 por 2 da 0 pero recuerda el signo menos
- nivel-2x2 3 por 2 da 1 pero con otra vez un signo menos
(hay cancelación de los dos signos menos así que el resultado es K301)
Podemos ahora comenzar a construir los conjuntos de matrices mutuamente anticonmutantes ortogonales, a veces llamadas las matrices de Dirac. Es obvio que dos tales matrices anticonmutan si anticonmutan en un número impar de índices (el índice 0 conmuta con el resto de índices).
K13 por ejemplo anticonmuta con
- K01, K02, K11, K12, K20, K23, K30, K33
y conmuta con
- K00, K10, K13, K21, K22, K31, K32.
Si el índice 2 aparece un número par de veces en el nombre entonces el cuadrado de la matriz es más (+) la matriz identidad, vamos a llamar a esto un Kplus
- ejemplos son K1, K22, K311, K2222
Si el índice 2 aparece un número impar de vecess en el nombre entonces el cuadrado de la matriz es menos (-) la matriz identidad, vamos a llamar a esto un Kminus
- ejemplos son K2, K222, K211, K1222
Ahora tenemos una manera muy simple de construir los conjuntos posibles más grandes de matrices anticonmutantes.
Comience con un conjunto existente {K1, K2, K3}
Inserte un nuevo índice constante (por ejemplo un 1 en la primera posición) y se obtiene {K11, K12, K13}
Entonces agregue dos matrices más que anticonmuten en el nuevo nivel y conmuten en el viejo nivel (por medio del índice cero 0)
Se consigue {K11, K12, K13, K20, K30}
Otros ejemplos
- {K21, K22, K23, K10, K30}
- {K31, K32, K33, K10, K20}
- {K111, K112, K113, K120, K130, K200, K300}
- {K211, K212, K213, K220, K230, K100, K300}
- {K311, K312, K313, K320, K330, K100, K200}
Se consigue siempre un conjunto con un número impar de matrices y hay siempre un Kplus más que Kminus.
Cada uno de ellas se puede escribir como el producto de todas las demás. Ejemplo K11 K12 K13 K20 = K30.
Álgebra de Clifford real R2,0
p = 2 y q = 0 por tanto necesitamos 2 Kplus como vectores base
grado 0 (el escalar)
grado 1 (los vectores)
grado 2 (el pseudoescalar)
n = p + q = 2 y se tienen 22 = 4 elementos así que es lo que I. Portious llama un álgebra universal de Clifford.
Álgebra de Clifford real R1,1
p = 1 y q = 1 necesitamos un Kplus y 1 Kminus como vectores base
grado 0 (el escalar)
grado 1 (los vectores)
grado 2 (el pseudoescalar)
Aquí tenemos otra vez 2n elementos en el álgebra con n = p+q así que es otra vez un álgebra universal de Clifford.
Álgebra de Clifford real R2,1
p = 2 y q = 1 necesitamos dos Kplus y 1 Kminus como vectores base
grado 0 (el escalar)
grado 1 (los vectores)
La signatura es (+ + -)
grado 2 (los bivectores)
grado 3 (el pseudoescalar)
Éste es el primer ejemplo de un álgebra no-universal de Clifford puesto que p+q = 3 y se tienen solamente 22 elementos y no 23. La razón es muy simple, cada matriz se utiliza dos veces, una vez como vector y una vez como bivector. Y el pseudoscalar es precisamente real como el escalar.
(el dual de Hodge de cada elemento es simplemente menos el original)
Álgebra de Clifford real R0,2
p = 0 y q = 2 necesitamos dos Kminus como vectores base, esto no es posible con matrices reales 2x2 así que necesitamos utilizar las matrices 4x4, tenemos muchas posibilidades. Esta álgebra es isomorfa con H (los cuaterniones)
grado 0 (el escalar)
grado 1 (los vectores)
La signatura es (- -)
grado 2 (el pseudoescalar)
El isomorfismo con los cuaterniones es como sigue
1 es escalar, i y j son vectores y k = el ij es el pseudoescalar.
Un número de Clifford es una combinación lineal de los 4 elementos 1 i j y k.
El uso de k como pseudoescalar (el producto de i por j) es un poco extraño pero perfectamente correcto.
Álgebra de Clifford real R0,3
p = 0 y q = 3 necesitamos 3 Kminus como vectores base, ésta es la manera usual de trabajar con cuaterniones i, j y k pero ahora son vectores base y el ijk = -1 es el pseudoescalar. Esta álgebra es otra vez isomorfa con H (los cuaterniones)
grado 0 (el escalar)
grado 1 (los vectores)
La signatura es (- - -)
grado 2 (los bivectores)
grado 3 (el pseudoescalar)
Un número de Clifford es aquí otra vez una combinación lineal de los 4 elementos 1 i j y k. el uso de -1 como pseudoescalar (los ijk) es el usual, solamente que hace del álgebra un nuevo ejemplo de un álgebra no-universal de Clifford, puesto que p + q = 3 y se tienen solamente 22 elementos.
Álgebra de Clifford real R3,0
Ésta es la famosa álgebra de Pauli, si se piensa en K02 como i y K00 como 1. Tenemos tres Kplus como vectores de base.
grado 0 (el escalar)
grado 1 (los vectores)
La signatura es (+ + +)
grado 2 (los bivectores)
grado 3 (el pseudoescalar)
Luego i es el pseudoscalar y las ecuaciones para los bivectores significan de hecho que cada bivector es la estrella de Hodge de un vector no parte del bivector.
Álgebra de Clifford real R3,1
Ésta es, tal vez, el álgebra de Clifford real más interesante porque permite la construcción de las ecuaciones tipo Dirac sin números complejos. Majorana la descubrió. Los espinores reales se llaman los espinores de Majorana. El álgebra también se conoce como el álgebra de Majorana. Hace uso de todas las 16 matrices reales 4x4.
Los cuatro vectores de base son de hecho las tres matrices de Pauli (Kplus) completadas con una cuarta matriz antihermitiana (Kmin).
La signatura es ( + + + - )
Para la signatura ( + - - - ) o ( - - - + ) comunmente usada en física se necesita matrices complejas 4x4 o matrices reales 8x8 porque no se puede formar 3 matrices 4x4 anticonmutantes Kmin.
vea R1,3 para algunas representaciones.
grado 0 (el escalar)
grado 1 (los vectores)
La signatura es (+ + + -)
grado 2 (los bivectores, las rotaciones de "árbol" y las "alzas" (boosts) de árbol)
grado 3 (los pseudovectores, los duales de Hodge de los vectores)
el último fue el pseudoescalar en R3,0
grado 4 (el pseudoescalar)

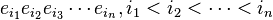
No hay comentarios:
Publicar un comentario