Análisis multifractal
El análisis multifractal se usa para caracterizar sistemas dinámicos, procesos o construcciones geométricas, asignándoles una función llamada espectro multifractal o espectro de singularidad. De acuerdo con el análisis multifractal de ciertos sistemas o procesos multifractales, las estructuras se caracterizan a través de una gama de dimensiones fractales diferentes asociadas a una jerarquía de subconjuntos, cada uno de ellos de carácter fractal.
El análisis multifractal permite caracterizaciones más precisas de un proceso que involucra fractales, ya que es un hecho conocido que la dimensión fractal por sí misma no caracteriza una estructura fractal por completo, en el sentido de que dos conjuntos de la misma dimensión fractal pueden no ser (bi-Lipschitz) equivalentes.

Introducción
Existen dos enfoques dentro del análisis multifractal:
- Las medidas multifractales, donde el carácter multifractal no se asocia a ningún conjunto concreto sino al comportamiento de una medida finita
 definida sobre todo
definida sobre todo 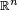 . La medida es multifractal cuando el conjunto
. La medida es multifractal cuando el conjunto  cuya dimensión fractal local es precisamente
cuya dimensión fractal local es precisamente  , tiene una dimensión fractal diferente de la dimensión fractal local. Eso se usa cuando existe una medida natural que resulte natural para representar cierto proceso.
, tiene una dimensión fractal diferente de la dimensión fractal local. Eso se usa cuando existe una medida natural que resulte natural para representar cierto proceso. - Los conjuntos multifractales, donde se considera un conjunto fijo pero se considera una familia uniparamétrica de dimensiones fractales diferentes. En este enfoque, el conjunto se considera multifractal cuando las diferentes dimensiones fractales del conjunto difieren pero en conjunto forman una función continua llamada espectro multifractal. Este enfoque se debe a que, aunque dos conjuntos que bi-Lipschitz equivalentes tienen la dimensión fractal, no es cierto que dos conjuntos de la misma dimensión fractal sean bi-Lipschitz equivalentes. Por tanto, una dimensión fractal por sí misma no caracteriza por completo a un conjunto.1
Conjuntos multifractales
Cuando se usa el enfoque de caracterizar un conjunto mediante una familia uniparamétrica de dimensiones, el conjunto multifractal se trata como una variedad topológica, frecuentemente un espacio métrico. Un conjunto multifractal, en ese sentido, es un conjunto cuya dimensión de Hausdorff-Besicovitch excede a su dimensión topológica ( , fractal "en el sentido de Mandelbrot"), pero cuyas dimensiones de Rényi superiores son diferentes de la dimensión de Hausdorff-Besicovitch. En un conjunto multifractal, la dimensión de Hausdorff-Besicovitch difiere de la dimensión de información y de la dimensión de correlación (que a su vez difieren entre sí).
, fractal "en el sentido de Mandelbrot"), pero cuyas dimensiones de Rényi superiores son diferentes de la dimensión de Hausdorff-Besicovitch. En un conjunto multifractal, la dimensión de Hausdorff-Besicovitch difiere de la dimensión de información y de la dimensión de correlación (que a su vez difieren entre sí).
 , fractal "en el sentido de Mandelbrot"), pero cuyas dimensiones de Rényi superiores son diferentes de la dimensión de Hausdorff-Besicovitch. En un conjunto multifractal, la dimensión de Hausdorff-Besicovitch difiere de la dimensión de información y de la dimensión de correlación (que a su vez difieren entre sí).
, fractal "en el sentido de Mandelbrot"), pero cuyas dimensiones de Rényi superiores son diferentes de la dimensión de Hausdorff-Besicovitch. En un conjunto multifractal, la dimensión de Hausdorff-Besicovitch difiere de la dimensión de información y de la dimensión de correlación (que a su vez difieren entre sí).
Un objeto multifractal es más complejo que un fractal simple autoescalante de dimensión fractal constante. Si un fractal de dimensión constante está complemente descrito por su dimensión fractal o exponente fractal (y en parte por su lagunaridad), la caracterización de un objeto multifractal requiere especificar un espectro de exponentes (llamado también espectro de singularidad).
Cualquier reunión de conjuntos fractales por sí sola no puede considerarse un multifractal; para ello es necesario que estén coordinados de cierta manera. Como norma general, se exige que el espectro de singularidad sea una curva convexa. El objetivo es garantizar que tanto el conjunto como cada una de sus partes sean invariantes bajo transformaciones de cambio de escala.
Los objetos aproximadamente multifractales son comunes en la Naturaleza y aparecen en geofísica, hidrodinámica (flujos turbulentos), astrofísica (evolución de lasmanchas solares) y cosmología (distribución de galaxias), así como en sistemas sociales (series temporales del mercado de valores).
Ejemplos en la Naturaleza
Flujos turbulentos
- El interés por los multifractales nace del estudio de las propiedades de los fluidos turbulentos con un alto número de Reynolds. Éstos son los llamados fluidos en régimen de Turbulencia Completamente Desarrollada. En esos casos, la elevada turbulencia del fluido hace que su estructura abandone todas las simetrías afinespropias del régimen laminar. A cualquier escala a la que se analice el fluido se encontrará que los grados de libertad no resueltos no son pequeñas variaciones ofluctuaciones sobre el régimen de mayor escala, sino que tienen amplitudes considerables, hasta el punto de que la dirección de la corriente está complemente indeterminada, aunque se conozca la dirección a una escala mayor.
Campo de velocidades en flujo turbulento (alta resolución) (baja resolución)
Distribución de galaxias
Otro ejemplo de multifractal es la distribución de galaxias. Las estimaciones disponibles sugieren que el Universo es más bien un objeto multifractal cuya dimensión de Hausdorff-Besicovitch sería D0 ~ 2,1±0,1 y cuya dimensión de correlación D2 ~ 1,3±0,1.2
Descripción
Dado un sistema multifractal y una magnitud física  medida sobre él tiene localmente un comportamiento cualitativo dado por una ley potencial de la forma:
medida sobre él tiene localmente un comportamiento cualitativo dado por una ley potencial de la forma:
 medida sobre él tiene localmente un comportamiento cualitativo dado por una ley potencial de la forma:
medida sobre él tiene localmente un comportamiento cualitativo dado por una ley potencial de la forma:
El exponente  se llama exponente de singularidad, ya que describe localmente el grado de singularidad o regularidad que presenta el comportamiento de la magnitud dada alrededor del punto
se llama exponente de singularidad, ya que describe localmente el grado de singularidad o regularidad que presenta el comportamiento de la magnitud dada alrededor del punto  . Es obvio, por ejemplo, que si
. Es obvio, por ejemplo, que si  , entonces la magnitud presentará discontinuidades, ya que la derivada no existe por culpa de que el límite que la define no es finito.
, entonces la magnitud presentará discontinuidades, ya que la derivada no existe por culpa de que el límite que la define no es finito.
 se llama exponente de singularidad, ya que describe localmente el grado de singularidad o regularidad que presenta el comportamiento de la magnitud dada alrededor del punto
se llama exponente de singularidad, ya que describe localmente el grado de singularidad o regularidad que presenta el comportamiento de la magnitud dada alrededor del punto  . Es obvio, por ejemplo, que si
. Es obvio, por ejemplo, que si  , entonces la magnitud presentará discontinuidades, ya que la derivada no existe por culpa de que el límite que la define no es finito.
, entonces la magnitud presentará discontinuidades, ya que la derivada no existe por culpa de que el límite que la define no es finito.
El conjunto formado por todos los puntos que comparten el mismo exponente de singularidad se llama "variedad de singularidad de exponente h". La variedad de singularidad de exponente h es un conjunto fractal de dimensión D(h). La curva definida como el grafo de la función D(h), es lo que se llama espectro de singularidad y describe completamente la distribución (estadística) de la magntiud  .
.
 .
.
En la práctica, sin embargo, el comportamiento de un sistema multifractal no se caracteriza directamente por su espectro de singularidad, sino más bien mediante losexponentes multiescala  . Frecuentemente los magnitudes medibles de sistemas multifractales siguen una ley de invariancia de escala asociada a leyes potenciales asociadas a la escala
. Frecuentemente los magnitudes medibles de sistemas multifractales siguen una ley de invariancia de escala asociada a leyes potenciales asociadas a la escala  . Dependiendo del objeto de estudio, dichas magnitudes denotadas mediante
. Dependiendo del objeto de estudio, dichas magnitudes denotadas mediante  suelen ser promedios locales en cajas de una retícula de lado
suelen ser promedios locales en cajas de una retícula de lado  o variaciones espaciales a una distancia
o variaciones espaciales a una distancia  , coneficientes de ondícula de escala
, coneficientes de ondícula de escala  , etc. Para objetos multifractales, se observa una ley potencial global de escalado de la forma:
, etc. Para objetos multifractales, se observa una ley potencial global de escalado de la forma:
 . Frecuentemente los magnitudes medibles de sistemas multifractales siguen una ley de invariancia de escala asociada a leyes potenciales asociadas a la escala
. Frecuentemente los magnitudes medibles de sistemas multifractales siguen una ley de invariancia de escala asociada a leyes potenciales asociadas a la escala  . Dependiendo del objeto de estudio, dichas magnitudes denotadas mediante
. Dependiendo del objeto de estudio, dichas magnitudes denotadas mediante  suelen ser promedios locales en cajas de una retícula de lado
suelen ser promedios locales en cajas de una retícula de lado  o variaciones espaciales a una distancia
o variaciones espaciales a una distancia  , coneficientes de ondícula de escala
, coneficientes de ondícula de escala  , etc. Para objetos multifractales, se observa una ley potencial global de escalado de la forma:
, etc. Para objetos multifractales, se observa una ley potencial global de escalado de la forma:
al menos en un rango de escalas relevante y para algunos rangos de orden  . Cuando un sistema presenta este comportamiento, se dice que presenta invariancia de escala, autosimilaridad o multiescalaridad.
. Cuando un sistema presenta este comportamiento, se dice que presenta invariancia de escala, autosimilaridad o multiescalaridad.
 . Cuando un sistema presenta este comportamiento, se dice que presenta invariancia de escala, autosimilaridad o multiescalaridad.
. Cuando un sistema presenta este comportamiento, se dice que presenta invariancia de escala, autosimilaridad o multiescalaridad.
ANÁLISIS FRACTAL Y MULTIFRACTAL .- ......................................:http://www.tesisenred.net/bitstream/handle/10803/6380/3_3_Analisis_Fractal.pdf?sequence=16
armónicos esféricos son funciones armónicas que representan la variación espacial de un conjunto ortogonal de soluciones de la ecuación de Laplace cuando la solución se expresa en coordenadas esféricas.
Los armónicos esféricos son importantes en muchas aplicaciones teóricas y prácticas, en particular en la física atómica (dado que la función de onda de los electrones contienen armónicos esféricos) y en la teoría del potencial que resulta relevante tanto para el campo gravitatorio como para la electrostática.
Introducción
La ecuación de Laplace en coordenadas esféricas viene dada por:
(véase también nabla y laplaciano en coordenadas esféricas). Si en esta expresión se consideran soluciones particulares de la forma,
 , la parte angular Y, se le denomina armónico esférico y satisface la relación:
, la parte angular Y, se le denomina armónico esférico y satisface la relación:Si a su vez se usa el método de separación de variables a esta última ecuación se puede ver que la ecuación anterior admite soluciones periódicas en las dos coordenadas angulares l es un número entero. Entonces la solución periódica del sistema anterior dependerá de los dos enteros (l, m) y vendrá dada en términos de funciones trigonométricas y de polinomios asociados de Legendre:
 ,
,
Donde
 se llama función armónica esférica de grado
se llama función armónica esférica de grado  y orden
y orden  ,
,  es el polinomio asociado de Legendre,
es el polinomio asociado de Legendre,  es una constante de normalización y
es una constante de normalización y  y
y  representan las variables angulares (el ángulo polar o colatitud y azimutal o longitud, respectivamente).
representan las variables angulares (el ángulo polar o colatitud y azimutal o longitud, respectivamente).
Las coordenadas esféricas utilizadas en este artículo son consistentes con las utilizadas por los físicos, pero difieren de las utilizadas por los matemáticos (vercoordenadas esféricas). En particular, la colatitud  , o ángulo polar, se encuentra en el rango
, o ángulo polar, se encuentra en el rango 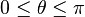 y la longitud
y la longitud  , o azimuth, posee el rango
, o azimuth, posee el rango  . Por lo tanto,
. Por lo tanto,  es 0 en el Polo Norte,
es 0 en el Polo Norte, 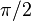 en el Ecuador, y
en el Ecuador, y  en el Polo Sur.
en el Polo Sur.
 , o ángulo polar, se encuentra en el rango
, o ángulo polar, se encuentra en el rango 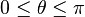 y la longitud
y la longitud  , o azimuth, posee el rango
, o azimuth, posee el rango  . Por lo tanto,
. Por lo tanto,  es 0 en el Polo Norte,
es 0 en el Polo Norte, 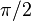 en el Ecuador, y
en el Ecuador, y  en el Polo Sur.
en el Polo Sur.Cuando la ecuación de Laplace se resuelve sobre un dominio esférico, las condiciones de periodicidad sobre la frontera en la coordenada
 así como las condiciones de regularidad en el "polo norte" y "sur" de la esfera, conllevan como se ha dicho que los números el grado l y el orden m necesarios para que se satisfagan deben ser enteros que cumplen:
así como las condiciones de regularidad en el "polo norte" y "sur" de la esfera, conllevan como se ha dicho que los números el grado l y el orden m necesarios para que se satisfagan deben ser enteros que cumplen:  y
y  .
.Normalización
Existen varias normalizaciones utilizadas para las funciones de armónicos esféricos. En física y sismología estas funciones son generalmente definidas como
donde
Estas funciones están ortonormalizadas
,
donde δaa = 1, δab = 0 si a ≠ b, (ver delta de Kronecker). Mientras que en las áreas de geodésica y análisis espectral se utiliza
que posee una potencia unitaria
 .
.
En temas de magnetismo, en cambio, se utilizan los armónicos de Schmidt semi-normalizados
poseen la siguiente normalización
 .
.
Utilizando la identidad (ver Polinomios asociados de Legendre)
se puede demostrar que todas las funciones armónicas esféricas normalizadas mencionadas en los párrafos anteriores satisfacen
 ,
,
donde el símbolo * significa conjugación compleja.
Convención de fase de Condon-Shortley
Una fuente de confusión con la definición de los esféricos armónicos es el factor de fase de  , comúnmente identificado como la fase de Condon-Shortley en la literatura relacionada con mecánica cuántica. En el área de mecánica cuántica, es práctica usual incluir este factor de fase en la definición de las funciones asociadas de Legendre, o acoplarlo a la definición de las funciones armónicas esféricas. No existe ningún requerimiento que obligue a utilizar la fase de Condon-Shortley en la definición de las funciones esféricas armónicas pero, si es que se la incluye, entonces algunas operaciones en el campo de la mecánica cuántica son más simples. Por el contrario en los campos de geodesia y magnetismo nunca se incluye el factor de fase de Condon-Shortley en la definición de los esféricos armónicos.
, comúnmente identificado como la fase de Condon-Shortley en la literatura relacionada con mecánica cuántica. En el área de mecánica cuántica, es práctica usual incluir este factor de fase en la definición de las funciones asociadas de Legendre, o acoplarlo a la definición de las funciones armónicas esféricas. No existe ningún requerimiento que obligue a utilizar la fase de Condon-Shortley en la definición de las funciones esféricas armónicas pero, si es que se la incluye, entonces algunas operaciones en el campo de la mecánica cuántica son más simples. Por el contrario en los campos de geodesia y magnetismo nunca se incluye el factor de fase de Condon-Shortley en la definición de los esféricos armónicos.
 , comúnmente identificado como la fase de Condon-Shortley en la literatura relacionada con mecánica cuántica. En el área de mecánica cuántica, es práctica usual incluir este factor de fase en la definición de las funciones asociadas de Legendre, o acoplarlo a la definición de las funciones armónicas esféricas. No existe ningún requerimiento que obligue a utilizar la fase de Condon-Shortley en la definición de las funciones esféricas armónicas pero, si es que se la incluye, entonces algunas operaciones en el campo de la mecánica cuántica son más simples. Por el contrario en los campos de geodesia y magnetismo nunca se incluye el factor de fase de Condon-Shortley en la definición de los esféricos armónicos.
, comúnmente identificado como la fase de Condon-Shortley en la literatura relacionada con mecánica cuántica. En el área de mecánica cuántica, es práctica usual incluir este factor de fase en la definición de las funciones asociadas de Legendre, o acoplarlo a la definición de las funciones armónicas esféricas. No existe ningún requerimiento que obligue a utilizar la fase de Condon-Shortley en la definición de las funciones esféricas armónicas pero, si es que se la incluye, entonces algunas operaciones en el campo de la mecánica cuántica son más simples. Por el contrario en los campos de geodesia y magnetismo nunca se incluye el factor de fase de Condon-Shortley en la definición de los esféricos armónicos.Definición matemática: Armónicos hiperesféricos
En matemáticas se usa una noción de armónico esférico más amplia que en física. Dado un polinomio P(x) homogéneo y armónico de grado m sobre  se denomina armónico esférico de grado m a la función obtenida como restricción de P(x) a la (n-1)-esfera
se denomina armónico esférico de grado m a la función obtenida como restricción de P(x) a la (n-1)-esfera  . Las funciones consideradas anteriormente
. Las funciones consideradas anteriormente  son obviamente ejemplos de funciones armónicas, pero también son ciertas combinaciones lineales de los mismos. Para n > 3 la definción anterior permite definir armónicos hiperesféricos, que generalizan la definción a espacios de dimensión superior.
son obviamente ejemplos de funciones armónicas, pero también son ciertas combinaciones lineales de los mismos. Para n > 3 la definción anterior permite definir armónicos hiperesféricos, que generalizan la definción a espacios de dimensión superior.
 se denomina armónico esférico de grado m a la función obtenida como restricción de P(x) a la (n-1)-esfera
se denomina armónico esférico de grado m a la función obtenida como restricción de P(x) a la (n-1)-esfera  . Las funciones consideradas anteriormente
. Las funciones consideradas anteriormente  son obviamente ejemplos de funciones armónicas, pero también son ciertas combinaciones lineales de los mismos. Para n > 3 la definción anterior permite definir armónicos hiperesféricos, que generalizan la definción a espacios de dimensión superior.
son obviamente ejemplos de funciones armónicas, pero también son ciertas combinaciones lineales de los mismos. Para n > 3 la definción anterior permite definir armónicos hiperesféricos, que generalizan la definción a espacios de dimensión superior.
Si  designa a todos las funciones armónicas de grado m, se pueden demostrar una serie de propiedades importantes:
designa a todos las funciones armónicas de grado m, se pueden demostrar una serie de propiedades importantes:
 designa a todos las funciones armónicas de grado m, se pueden demostrar una serie de propiedades importantes:
designa a todos las funciones armónicas de grado m, se pueden demostrar una serie de propiedades importantes:- El espacio de funciones de cuadrado integrable sobre la n-esfera es suma directa de espacios anteriores

- Dados dos espacios
 y
y  con
con  , entonces esos dos espacios son ortogonales.
, entonces esos dos espacios son ortogonales. - La dimensión del espacio
 viene dada por:
viene dada por:
Expansión en armónicos esféricos
Los armónicos esféricos forman un conjunto completo ortonormal de funciones y por lo tanto forman un espacio vectorial análogo a vectores unitarios de la base. Sobre la esfera unitaria, toda función de cuadrado integrable puede, por lo tanto, ser expandida como una combinación lineal de:
 .
.
Esta expansión es exacta siempre y cuando  se extienda a infinito. Se producirá un error de truncamiento al limitar la suma sobre
se extienda a infinito. Se producirá un error de truncamiento al limitar la suma sobre  a un ancho de banda finito
a un ancho de banda finito  . Los coeficientes de la expansión
. Los coeficientes de la expansión  pueden obtenerse multiplicando la ecuación precedente por el complejo conjugado de los esféricos armónicos, integrando sobre un ángulo sólido
pueden obtenerse multiplicando la ecuación precedente por el complejo conjugado de los esféricos armónicos, integrando sobre un ángulo sólido  , y utilizando las relaciones de ortogonalidad indicadas previamente. Para el caso de armónicos ortonormalizados, se obtiene
, y utilizando las relaciones de ortogonalidad indicadas previamente. Para el caso de armónicos ortonormalizados, se obtiene
 se extienda a infinito. Se producirá un error de truncamiento al limitar la suma sobre
se extienda a infinito. Se producirá un error de truncamiento al limitar la suma sobre  a un ancho de banda finito
a un ancho de banda finito  . Los coeficientes de la expansión
. Los coeficientes de la expansión  pueden obtenerse multiplicando la ecuación precedente por el complejo conjugado de los esféricos armónicos, integrando sobre un ángulo sólido
pueden obtenerse multiplicando la ecuación precedente por el complejo conjugado de los esféricos armónicos, integrando sobre un ángulo sólido  , y utilizando las relaciones de ortogonalidad indicadas previamente. Para el caso de armónicos ortonormalizados, se obtiene
, y utilizando las relaciones de ortogonalidad indicadas previamente. Para el caso de armónicos ortonormalizados, se obtiene .
.
Un conjunto alternativo de armónicos esféricos para funciones reales puede ser obtenido a partir del conjunto
Estas funciones tienen las mismas propiedades de normalización que las funciones complejas indicadas previamente. En esta notación, una función real integrable puede ser expresada como una suma de armónicos esféricos de infinitos términos como
 .
.
Armónicos Esféricos en física
A continuación mencionaremos algunas aplicaciones de los armónicos esféricos en física, tanto en electrostática como en mecánica cuántica.
Armónicos esféricos en electrostática
El átomo de hidrógeno
El moderno modelo atómico cuántico del átomo de hidrógeno presupone que cada electrón en un estado estacionario de energía del electrón tiene una posición que se distribuye alrededor del núcleo atómico con una distribución de probabilidad cuya variación angular viene dada por un armónico esférico.
Análisis espectral
La potencia total de una función  es definida en la literatura de procesamiento de señales electrónicas como la integral de la función elevada al cuadrado, dividida por el área que abarca. Usando las propiedades de ortonormalidad de las funciones armónicas esféricas de potencia real unitaria, es fácil verificar que la potencia total de una función definida sobre la esfera unitaria se relaciona con sus coeficientes espectrales a través de una generalización del teorema de Parseval:
es definida en la literatura de procesamiento de señales electrónicas como la integral de la función elevada al cuadrado, dividida por el área que abarca. Usando las propiedades de ortonormalidad de las funciones armónicas esféricas de potencia real unitaria, es fácil verificar que la potencia total de una función definida sobre la esfera unitaria se relaciona con sus coeficientes espectrales a través de una generalización del teorema de Parseval:
 es definida en la literatura de procesamiento de señales electrónicas como la integral de la función elevada al cuadrado, dividida por el área que abarca. Usando las propiedades de ortonormalidad de las funciones armónicas esféricas de potencia real unitaria, es fácil verificar que la potencia total de una función definida sobre la esfera unitaria se relaciona con sus coeficientes espectrales a través de una generalización del teorema de Parseval:
es definida en la literatura de procesamiento de señales electrónicas como la integral de la función elevada al cuadrado, dividida por el área que abarca. Usando las propiedades de ortonormalidad de las funciones armónicas esféricas de potencia real unitaria, es fácil verificar que la potencia total de una función definida sobre la esfera unitaria se relaciona con sus coeficientes espectrales a través de una generalización del teorema de Parseval: ,
,
donde
se define como el espectro de potencia angular. En forma similar, se puede definir la potencia cruzada entre dos funciones como
 ,
,
donde
se define como el espectro cruzado en este caso. Si las funciones  y
y  tienen un valor promedio igual a cero (o sea los coeficientes espectrales
tienen un valor promedio igual a cero (o sea los coeficientes espectrales  y
y  son nulos), entonces
son nulos), entonces  y
y  representan las contribuciones a la varianza y covarianza de la función para el grado
representan las contribuciones a la varianza y covarianza de la función para el grado  , respectivamente. Es común que el espectro de potencia cruzado se pueda aproximar por una power law del tipo
, respectivamente. Es común que el espectro de potencia cruzado se pueda aproximar por una power law del tipo
 y
y  tienen un valor promedio igual a cero (o sea los coeficientes espectrales
tienen un valor promedio igual a cero (o sea los coeficientes espectrales  y
y  son nulos), entonces
son nulos), entonces  y
y  representan las contribuciones a la varianza y covarianza de la función para el grado
representan las contribuciones a la varianza y covarianza de la función para el grado  , respectivamente. Es común que el espectro de potencia cruzado se pueda aproximar por una power law del tipo
, respectivamente. Es común que el espectro de potencia cruzado se pueda aproximar por una power law del tipo .
.
Cuando 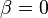 , el espectro es "blanco" dado que cada grado posee idéntica potencia. Cuando
, el espectro es "blanco" dado que cada grado posee idéntica potencia. Cuando  , el espectro se denomina "rojo" ya que existe mayor potencia a grados bajos con longitudes de onda largas que a altos grados. Finalmente, cuando
, el espectro se denomina "rojo" ya que existe mayor potencia a grados bajos con longitudes de onda largas que a altos grados. Finalmente, cuando  , el espectro es denominado "azul".
, el espectro es denominado "azul".
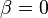 , el espectro es "blanco" dado que cada grado posee idéntica potencia. Cuando
, el espectro es "blanco" dado que cada grado posee idéntica potencia. Cuando  , el espectro se denomina "rojo" ya que existe mayor potencia a grados bajos con longitudes de onda largas que a altos grados. Finalmente, cuando
, el espectro se denomina "rojo" ya que existe mayor potencia a grados bajos con longitudes de onda largas que a altos grados. Finalmente, cuando  , el espectro es denominado "azul".
, el espectro es denominado "azul".Teorema de la suma
Un resultado matemático de sumo interés y utilidad es el llamado teorema de la suma para los armónicos esféricos. Dos vectores r y r', con coordenadas esféricas  y
y  , respectivamente, tienen un ángulo
, respectivamente, tienen un ángulo  entre ellos dado por la expresión
entre ellos dado por la expresión
 y
y  , respectivamente, tienen un ángulo
, respectivamente, tienen un ángulo  entre ellos dado por la expresión
entre ellos dado por la expresión .
.
El teorema de la suma expresa un polinomio de Legendre de orden  en el ángulo
en el ángulo  en términos de los productos de dos armónicos esféricos con coordenadas angulares
en términos de los productos de dos armónicos esféricos con coordenadas angulares y
y  :
:
 en el ángulo
en el ángulo  en términos de los productos de dos armónicos esféricos con coordenadas angulares
en términos de los productos de dos armónicos esféricos con coordenadas angulares y
y  :
: .
.
Esta expresión es válida tanto para los armónicos reales como para los complejos. Sin embargo, debe enfatizarse que la fórmula indicada previamente es válida solo para armónicos esféricos ortonormalizados. Para armónicos de potencia unitaria es necesario eliminar el factor 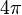 de la expresión anterior.
de la expresión anterior.
 de la expresión anterior.
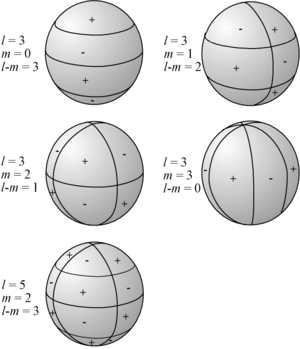
de la expresión anterior.Visualización de los armónicos esféricos
Los armónicos esféricos son fáciles de visualizar contando el número de cruces por cero que ellos tienen tanto en dirección de las latitudes como de las longitudes. Para la dirección en las latitudes, las funciones asociadas de Legendre tienen  ceros, mientras que en sentido longitudinal, las funciones trigonometricas seno y cosenotienen
ceros, mientras que en sentido longitudinal, las funciones trigonometricas seno y cosenotienen  ceros.
ceros.
 ceros, mientras que en sentido longitudinal, las funciones trigonometricas seno y cosenotienen
ceros, mientras que en sentido longitudinal, las funciones trigonometricas seno y cosenotienen  ceros.
ceros.
Cuando el armónico esférico de orden  es nulo o cero, las funciones armónicas esféricas no dependen de la longitud, y se dice que la función es zonal. Cuando
es nulo o cero, las funciones armónicas esféricas no dependen de la longitud, y se dice que la función es zonal. Cuando  , no existen cruces por cero en sentido de las latitudes, y se dice que la función es sectorial. Para otro casos, las funciones forman un damero sobre la esfera.
, no existen cruces por cero en sentido de las latitudes, y se dice que la función es sectorial. Para otro casos, las funciones forman un damero sobre la esfera.
 es nulo o cero, las funciones armónicas esféricas no dependen de la longitud, y se dice que la función es zonal. Cuando
es nulo o cero, las funciones armónicas esféricas no dependen de la longitud, y se dice que la función es zonal. Cuando  , no existen cruces por cero en sentido de las latitudes, y se dice que la función es sectorial. Para otro casos, las funciones forman un damero sobre la esfera.
, no existen cruces por cero en sentido de las latitudes, y se dice que la función es sectorial. Para otro casos, las funciones forman un damero sobre la esfera.Ejemplos de los primeros armónicos esféricos
Expresiones analíticas de los primeros armónicos esféricos ortonormalizados, que usan la convención de fase de Condon-Shortley:
Generalizaciones
El mapa de los armónicos esféricos puede ser visto como representaciones de la simetría de grupo de rotaciones alrededor de un punto (SO(3)) y recubridor universalSU(2). Por lo tanto, capturan la simetría de la esfera de dos dimensiones. Cada grupo de armónicos esféricos con un valor dado del parámetro l da lugar a una representación irreductible diferente del grupo SO(3).
Además, la esfera es equivalente a la esfera de Riemann. El conjunto completo de simetrías de la esfera de Riemann se describen mediante el grupo de transformaciones de Möbius PSL(2,C), que es isomorfo al grupo de Lie real llamado grupo de Lorentz. El análogo del los armónicos esféricos con respecto al grupo de Lorentz es la serie hipergeométrica; de hecho, los armónicos esféricos pueden reescribirse en términos de la serie hipergeométrica, dado que SO(3) es un subgrupo de PSL(2,C).
Más específicamente, se puede generalizar a la serie hipergeométrica para describir las simetrías de cualquier espacio de simetría; en particular, la serie hipergeométrica puede ser desarrollada para todo grupo de Lie.
Problemas
Arm´onicos Esf´ericos § .- .........................................................:http://users.df.uba.ar/dmitnik/teoricaII/sphericalh/spherical.pdf



























No hay comentarios:
Publicar un comentario