miércoles, 11 de noviembre de 2015

Física matemática

Mecánica routhiana


la mecánica routhiana es una formulación híbrida de mecánica lagrangiana y la Mecánica hamiltoniana desarrollada por Edward John Routh. De la misma manera , el routhiano es la función que  reemplaza a ambas las funciones lagrangianas y hamiltonianas.
El Routhiano, como el hamiltoniano, puede ser obtenido de un Transformada de Legendre del lagrangiano, y tiene una forma matemática similar al hamiltoniano, pero no es exactamente igual. La diferencia entre el lagrangiano, hamiltoniano, y routhiano  son sus variables . Para un conjunto dado de Coordenadas generalizadas representando los grados de libertad en el sistema, el lagrangiano es una función de las coordenadas y velocidades, mientras el hamiltoniano es una función de las coordenadas y momentos.
El routhiano difiere de estas funciones en que  algunas coordenadas están escogidas para tener correspondientes  velocidades generalizadas, el resto para tener correspondientes momentos generalizados. Esta elección es arbitraria, y puede ser hecha para simplificar el problema. También tiene la consecuencia de que las ecuaciones de routh son exactamente las ecuaciones hamiltonianas para algunas coordenadas y sus momentos correspondientes, y las ecuaciones lagrangianas para el resto de las coordenadas y sus velocidades. En este caso las funciones lagrangianas y hamiltonianas están reemplazadas por una única función, el routhiano. El conjunto total tiene así las ventajas de ambos conjuntos de ecuaciones, con la comodidad de partir un conjunto de coordenadas a las ecuaciones hamiltonianas, y el resto a las ecuaciones lagrangianas.
A menudo la aproximación routhiana puede no ofrecer ninguna ventaja nueva, pero un caso notable donde esto es útil es cuándo un sistema tiene coordenadas cíclicas (también llamadas "coordenadas ignorables"), por definición aquellas coordenadas no aparecen en el lagrangiano original. Las ecuaciones lagrangianas son resultados poderosos , utilizadas frecuentemente en teoría y práctica, ya que las ecuaciones del movimiento  son fácil de establecer en las coordenadas. Aun si hay coordenadas cíclicas todavía habrá ecuaciones por resolver para todas las coordenadas, incluyendo las cíclicas a pesar de su ausencia en el lagrangiano. Las ecuaciones hamiltonianas son resultados teóricos útiles , pero menos útiles en la práctica porque las coordenadas y los momentos están relacionados juntos en las soluciones - después de solucionar las ecuaciones las coordenadas y los momentos tienen que ser eliminados uno del otro. No obstante, las ecuaciones hamiltonianas son perfectamente convenientes  para coordenadas cíclicas porque las ecuaciones en las coordenadas cíclicas desaparecen trivialmente, dejando sólo las ecuaciones en las coordenadas no cíclicas.
La aproximación routhiana tiene lo mejor de ambas aproximaciones, porque las coordenadas pueden ser separadas hacia las ecuaciones hamiltonianas y eliminadas, dejando detrás las coordenadas no cíclicas para ser solucionadas a partir de las ecuaciones lagrangianas. En general menos ecuaciones necesitan  ser solucionadas comparada con la aproximación lagrangiana. Además, el método routhiano hace más claro las interpretaciones físicas de las constantes asociadas con coordenadas cíclicas, en la aproximación lagrangiana las constantes son menos obvias.
Con el resto de mecánica analítica, la mecánica routhiana es completamente equivalente a la mecánica newtoniana, y a otras formulaciones de mecánica clásica, y no introduce física nueva. Ofrece una manera alternativa de solucionar problemas mecánicos.

Definiciones

En el caso de la mecánica langrariana,el langrariano es función de las coordenadas generalizadas q1, q2, ... , las correspondientes velocidades dq1/dt, dq2/dt, ...,y posiblemente el tiempo t, 
L(q_1,q_2,\ldots,\dot{q}_1,\dot{q}_2,\ldots,t)\,, \quad \dot{q}_i = \frac{d q_i}{dt} \,,
donde los puntos por encima denotan derivadas con respecto al tiempo.
En mecánica hamiltoniana, las coordenadas generalizadas q1, q2, ... y los correspondientes momentos generalizadas p1, p2, ..., y posiblemente el tiempo, forman al hamiltoniano
H(q_1,q_2,\ldots,p_1,p_2,\ldots,t) = \sum_i \dot{q}_ip_i - L(q_1,q_2,\ldots,\dot{q}_1(p_1),\dot{q}_2(p_2),\ldots,t) \,, \quad p_i = \frac{\partial L}{\partial \dot{q}_i}\,,
donde la segunda ecuación es la definición del momento generalizado pi de la coordenada qi (derivadas parciales son denotadas usando ∂). Las velocidades dqi/dt son expresadas como funciones de sus momentos correspondientes al invertir la relación que las define . En este contexto ,se dice que pi es el momento "canónicamente conjugado" de qi.
El routhiano es intermedio entre L y H; algunas coordenadas q1, q2, ..., qn son elegidas para tenefr el correspondiente momento generalizado p1, p2, ..., pn, el resto de las coordenadas ζ1, ζ2, ..., ζs para tener velocidades generalizadas dζ1/dt, dζ2/dt, ..., dζs/dt y el tiempo puede aparecer explícitamente; 1 2
donde otra vez la velocidad generalizada dqi/dt es expresada como función del momento generalizado pi via su relación de definición. La elección de cuales ncoordenadas tendrán el correspondiente momento, dentro de las  n + s coordenadas es arbitraria.
Lo anterior es utilizado por Landau y Lifshitz, y Goldstien. Algunos autores pueden definir el routhiano para ser el negativo de la definición anterior.3
Dada la longitud de la definición general,una notación más compacta utiliza negritas para n-adas (o vectores) de las variables, así q = (q1, q2, ..., qn), ζ = (ζ1, ζ2, ..., ζs),p = (p1, p2, ..., pn), y d ζ/dt = (dζ1/dt, dζ2/dt, ..., dζs/dt), de manera que
R(\mathbf{q},\boldsymbol{\zeta}, \mathbf{p}, \dot{\boldsymbol{\zeta}}, t) = \mathbf{p}\cdot\dot{{\mathbf{q}}} - L(\mathbf{q}, \boldsymbol{\zeta}, \dot{\mathbf{q}}, \dot{\boldsymbol{\zeta}},t) \,,
donde · Es el producto de punto definido en n-adas, para el ejemplo concreto que aparece aquí:
\mathbf{p}\cdot\dot{{\mathbf{q}}} = \sum_{i=1}^n p_i\dot{q}_i \,.

Ecuaciones de movimiento

Para referencia, las ecuaciones lagrangianas para s los grados de libertad son un conjunto de s ecuaciones diferenciales normales de segundo orden acopladas en las coordenadas
\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_j} = \frac{\partial L}{\partial q_j} \,,
donde j = 1, 2, ..., s = 1, 2n, ..., j = 1, 2, ..., s, y las ecuaciones hamiltonianas para n los grados de libertad son un conjunto de 2n ecuaciones diferenciales ordinarioas de primer orden acopladas en las coordenadas y momentos
\dot{q}_i = \frac{\partial H}{\partial p_i} \,,\quad \dot{p}_i = -\frac{\partial H}{\partial q_i} \,.
Abajo, las ecuaciones de movimiento routhianas están obtenidas en dos maneras, en el proceso otras derivadas útiles son encontradas que pueden ser utilizadas en otro lugar.

Dos grados de libertad

Considere el caso de un sistema con dos grados de libertad, q y ζ, con velocidades generalizadas dq/dt y dζ/dt, y el lagrangiano dependiente del tiempo. (La generalización a cualquier número de los grados de libertad sigue exactamente el mismo procedimiento como con dos).4 El lagrangiano del sistema tendrá la forma
L(q, \zeta, \dot{q}, \dot{\zeta}, t)
El diferencial de L es
dL = \frac{\partial L}{\partial q}dq + \frac{\partial L}{\partial \zeta}d\zeta + \frac{\partial L}{\partial \dot{q}}d\dot{q} + \frac{\partial L}{\partial \dot{\zeta}}d\dot{\zeta} + \frac{\partial L}{\partial t}dt \,.

Ahora cambie las variables, del conjunto (q, ζ, dq/dt, dζ/dt) a (q, ζ, p, dζ/dt), sencillamente cambiando la velocidad dq/dt al momento p. Este cambio de variables en los diferenciales es la transformación de Legendre. EL diferencial de la función nueva para reemplazar L será una suma de diferenciales en dq, dζ, dp, d(dζ/dt), y dt. Utilizando la definición de la ecuación de Lagrange y momento generalizados para la coordenada q:

p = \frac{\partial L}{\partial \dot{q}} \,,\quad \dot{p} = \frac{d}{dt}\frac{\partial L}{\partial \dot{q}} = \frac{\partial L}{\partial q}
Tenemos
dL = \dot{p}dq + \frac{\partial L}{\partial \zeta}d\zeta + p d\dot{q} + \frac{\partial L}{\partial \dot{\zeta}}d\dot{\zeta} + \frac{\partial L}{\partial t}dt

Y para reemplazar pd(dq/dt) por (dq/dt)dp, recordar la regla de producto para diferenciales, y sustuirnb 1
pd\dot{q} = d(\dot{q} p) - \dot{q}dp
Para obtener el diferencial de una función nueva en términos del conjunto nuevo de variables:
d(L-p\dot{q}) = \dot{p} dq + \frac{\partial L}{\partial \zeta}d\zeta - \dot{q} dp + \frac{\partial L}{\partial \dot{\zeta}}d\dot{\zeta} + \frac{\partial L}{\partial t}dt \,.
Introduciendo el routhiano
R(q,\zeta,p,\dot{\zeta},t) = p \dot{q}(p) - L
donde otra vez la velocidad dq/dt es una función del momento p, tenemos
dR = -\dot{p} dq - \frac{\partial L}{\partial \zeta}d\zeta + \dot{q}dp - \frac{\partial L}{\partial \dot{\zeta}}d\dot{\zeta} - \frac{\partial L}{\partial t}dt\,,
Pero de la definición anterior, el diferencial del Routhian es
dR = \frac{\partial R }{\partial q}dq + \frac{\partial R }{\partial \zeta}d\zeta + \frac{\partial R }{\partial p}dp + \frac{\partial R }{\partial \dot{\zeta}}d\dot{\zeta} + \frac{\partial R}{\partial t}dt \,.
Comparando los coeficientes de los diferenciales dq, dζ, dp, d(dζ/d(dζ/dt)), y dt, los resultados son ecuaciones de hamilton para la coordenada q,
\dot{q} = \frac{\partial R}{\partial p} \,,\quad \dot{p} = -\frac{\partial R}{\partial q} \,,
Y la ecuación de Lagrange para la coordenada ζ

\frac{d}{dt}\frac{\partial R}{\partial \dot{\zeta}} = \frac{\partial R}{\partial \zeta}
que sigue de
\frac{\partial L}{\partial \zeta} = - \frac{\partial R}{\partial \zeta} \,,\quad \frac{\partial L}{\partial \dot{\zeta}} = - \frac{\partial R}{\partial \dot{\zeta}} \,,
Y tomando la derivada total del tiempo total de la segunda ecuación y equiparando a la primera. Nótese que el routhiano reemplaza las funciones hamiltonianas y lagrangianas en todas las ecuaciones de movimiento.
La ecuación Restante declara las derivadas parciales respecto al tiempo de L y R son negativas entre sí
\frac{\partial L}{\partial t}=-\frac{\partial R}{\partial t}\,.

Cualquier número de grados de libertad

Para n + s n + s n + s coordenadas como se definió encima, con el routhiano
R(q_1,\ldots,q_n,\zeta_1,\ldots,\zeta_s, p_1, \ldots,p_n , \dot{\zeta}_1 , \ldots,\dot{\zeta}_s,t) = \sum_{i=1}^n p_i\dot{q}_i(p_i) - L
Las ecuaciones de movimiento pueden ser obtenidas por una transformación de Legendre de este routhiano como en la sección anterior, pero otra manera es sencillamente tomar las derivadas parciales de R con respecto a las coordenadas qiqi y ζζj, momentos pi pi, y velocidades dζj/dt, donde i = 1, 2, ..., n, y j = 1, 2, ..., s. Las derivadas son:
\frac{\partial R}{\partial q_i} = -\frac{\partial L}{\partial q_i} = - \frac{d}{dt}\frac{\partial L}{\partial \dot{q}_i} = - \dot{p}_i \,
\frac{\partial R}{\partial p_i} = \dot{q}_i \,
\frac{\partial R}{\partial \zeta_j} = - \frac{\partial L}{\partial \zeta_j} \,,
\frac{\partial R}{\partial \dot{\zeta}_j} = - \frac{\partial L}{\partial \dot{\zeta}_j} \,,
\frac{\partial R}{\partial t} = - \frac{\partial L}{\partial t} \,.
Las primeras dos son identicas a las ecuaciones hamiltonianas. Equiparando la derivada total con respecto al tiempo del cuarto conjunto de ecuaciones con el tercero (para cada valor de j) da las ecuaciones lagrangianas. El quinto es justo la misma relación entre derivadas parciales del tiempo de antes. Para resumir5

El número total de ecuaciones es 2n + s, donde 2n son ecuaciones hamiltonianas y s ecuaciones langrarianas.







Número adimensional


Número adimensional es un número que no tiene unidades físicas que lo definan y por lo tanto es un número puro. Los números adimensionales se definen como productos o cocientes de cantidades que sí tienen unidades de tal forma que todas éstas se simplifican. Dependiendo de su valor estos números tienen un significado físico que caracteriza unas determinadas propiedades para algunos sistemas.

Teorema π de Vaschy-Buckingham

De acuerdo al Teorema π de Vaschy-Buckingham de análisis dimensional, la dependencia funcional entre un cierto número de variables (n) puede ser reducida en elnúmero de dimensiones independientes de esas n variables (k) para dar un número de cantidades adimensionales independientes (p = n - k). Así diferentes sistemas son equivalentes cuando tienen la misma descripción mediante números adimensionales.

Lista de números adimensionales

Existe una gran cantidad de números adimensionales, algunos de los más utilizados se listan aquí alfabéticamente.
NombreCampo de aplicación
Número de Abbeóptica (dispersión en materiales ópticos)
Número de Arquímedesmovimiento de fluidos debido a diferencias de densidad
Número de Bagnoldflujo de granos, arena, etc.
Número de Biotconductividad superficial vs. volumétrica de sólidos
Número de Bodensteindistribución del tiempo de residencia
Número de Bondfuerza capilar debido a la flotación
Número de Brinkmantransferencia de calor por conducción entre una superficie y un líquido viscoso
Número de Brownell Katzcombinación del número de capilaridad y el número de Bond
Número de Capilaridadflujo debido a la tensión superficial
Número de Courant-Friedrich-Levyresolución numérica de ecuaciones diferenciales
Número de Damköhlerescala de tiempo de un reacción química vs. el fenómeno de transporte
Número de Deanvórtices en tuberías curvas
Número de Deborahreología de los fluidos viscoelásticos
Número de Eckerttransferencia de calor por convección
Número de Ekmangeofísica (fuerzas de rozamiento por viscosidad)
Número de Eötvösdeterminación de la forma de la burbuja/gota
Número de Eulerhidrodinámica (fuerzas de presión vs. fuerzas inerciales)
Número de Foppl–von Karmanpandeo de cáscaras delgadas
Número de Fouriertransferencia de calor
Número de Fresneldifracción
Número de Froudefuerzas inerciales vs. gravitacionales en fluidos
Número de Galileiflujo viscoso debido a la gravedad
Número de Graetzflujo de calor
Número de Grashofconvección natural
Número de Hagenconvección forzada
Número de Karlovitzcombustión turbulenta
Número de Knudsenaproximación del continuo en fluidos
Número de Laplaceconvección natural en fluidos con mezclabilidad
Número de Lewisdifusión molecular vs. difusión térmica
Número de Machdinámica de los gases (velocidad del gas vs. velocidad del sonido)
Número de Reynolds magnéticomagnetohidrodinámica
Número de MarangoniFlujo de Marangoni
Número de Mortondeterminación de la forma de la burbuja/gota
Número de Nusselttransferencia de calor con convección forzada
Número de Ohnesorgeatomización de líquidos, flujo de Marangoni
Número de Pécletproblemas de advección–difusión
Número de Peeladhesión de microestructuras sobre sustratos
Número de Prandtlconvección forzada y natural
Número de Rayleighfuerzas de flotación y viscosas en convección natural
Número de Reynoldsfuerzas de inercia vs. viscosas en fluidos
Número de Richardsonefecto de la flotación en la estabilidad de los flujos
Número de Rossbyfuerzas inerciales en geofísica
Número de Schmidtdinámica de fluidos (transferencia de masa y difusión)
Número de Sherwoodtransferencia de masa y convección forzada
Número de Sommerfeldlubricación de bordes
Número de Stantontransferencia de calor con convección forzada
Número de Stefantransferencia de calor durante cambios de fase
Número de Stokesdinámica de la partícula
Número de Strouhalflujos continuos y pulsantes
Número de Taylorflujos rotacionales
Número de WagnerElectrodeposiciones
Número de Weberflujos multifásicos sobre superficies curvas
Número de Weissenbergflujos viscoelásticos
Número de Womersleyflujos continuos y pulsantes
Publicado por en

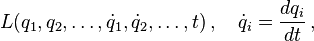
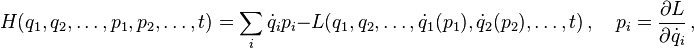
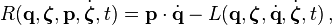
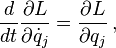
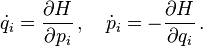
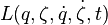
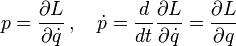
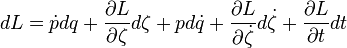
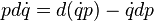
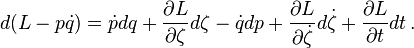
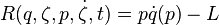
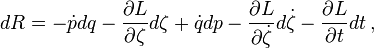
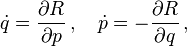
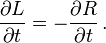
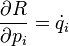
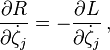
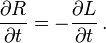
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)