Integrales típicas en teoría cuántica de campos
integrales típicas en teoría cuántica de campos que aparecen continuamente al aplicarla a los problemas concretos de la teoría.1 Estas integrales son todas variaciones y generalizaciones de integrales gaussianas en el plano complejo y en varias (muchas, o incluso infinitas) dimensiones. Otro conjunto de integrales pueden ser aproximadas por integrales gaussianas. También se presentan transformaciones de Fourier.
Integral gaussiana en una dimensión
Integral Gaussiana
La primera integral aquí presentada, de uso común también en aplicaciones diferentes a la teoría cuántica de campos, es la integral gaussiana, que es la integral sobre todo su dominio de la campana de Gauss.
En Física, es habitual usar un factor 1/2 en el argumento de la exponencial.
La forma usual de resolver esta integral es intentando resolver su versión bidimensional haciendo uso de la propiedad de factorización de la integral respecto a la suma de argumentos y de un cambio de variables de cartesianas a polares:
Con lo que se obtiene el resultado buscado
Una minúscula generalización de la integral gaussiana
donde hemos reescalado la variable
 .
.
Integrales de gaussianas con potencias pares de x
y
En general:
Nótese que, en el caso en el que tengamos potencias impares de x, la integral se anula debido a la simetría impar del argumento, por lo que
Integrales con un término lineal en el argumento de la exponencial
Esta integral se puede resolver completando el cuadrado.
Integrales con un término lineal imaginario en el argumento de la exponencial
La integral
es proporcional a la transformada de Fourier de la campana de Gauss, donde  es la variable conjugada de
es la variable conjugada de  .
.
 es la variable conjugada de
es la variable conjugada de  .
.
Se puede resolver como el caso anterior completando cuadrados, viendo así que la transformada de Fourier de una gaussiana es también otra guassiana, pero de la variable conjugada. Cuando mayor es el valor de  , más estrecha es la guassiana en
, más estrecha es la guassiana en  y más amplia es la gaussiana en
y más amplia es la gaussiana en  . Este es un caso particular del principio de incertidumbre.
. Este es un caso particular del principio de incertidumbre.
 , más estrecha es la guassiana en
, más estrecha es la guassiana en  y más amplia es la gaussiana en
y más amplia es la gaussiana en  . Este es un caso particular del principio de incertidumbre.
. Este es un caso particular del principio de incertidumbre.Integrales con un argumento complejo en el exponente
La integral de interés es (para ver un ejemplo de uso, véase Relación entre la ecuación de Schödinger y la formulación de la integral de camino de la mecánica cuántica).
Ahora asumimos que  y
y  pueden ser complejos.
pueden ser complejos.
 y
y  pueden ser complejos.
pueden ser complejos.
Completando el cuadrado
Por analogía con las integrales previas
Este resultado es válido como una integración en el plano complejo siempre que  tenga una para imaginaria positiva (por muy pequeña que esta sea).
tenga una para imaginaria positiva (por muy pequeña que esta sea).
 tenga una para imaginaria positiva (por muy pequeña que esta sea).
tenga una para imaginaria positiva (por muy pequeña que esta sea).Integrales gaussianas en varias dimensiones
La integral gaussiana unidimensional puede ser generalizada a  dimensiones.2
dimensiones.2
 dimensiones.2
dimensiones.2
Donde  es una matriz simétrica real.
es una matriz simétrica real.
 es una matriz simétrica real.
es una matriz simétrica real.
Esta integral se resuelve por medio de una diagonalización de la matriz  por medio de una transformación ortogonal
por medio de una transformación ortogonal
 por medio de una transformación ortogonal
por medio de una transformación ortogonal
donde  es una matriz diagonal y
es una matriz diagonal y  es una matriz ortogonal. Esta transformación desacopla las variables de integración, por lo que tenemos
es una matriz ortogonal. Esta transformación desacopla las variables de integración, por lo que tenemos  integrales unidomensionales que podemos resolver una a una independientemente.
integrales unidomensionales que podemos resolver una a una independientemente.
 es una matriz diagonal y
es una matriz diagonal y  es una matriz ortogonal. Esta transformación desacopla las variables de integración, por lo que tenemos
es una matriz ortogonal. Esta transformación desacopla las variables de integración, por lo que tenemos  integrales unidomensionales que podemos resolver una a una independientemente.
integrales unidomensionales que podemos resolver una a una independientemente.
Esto quedará seguramente más claro con un ejemplo en el caso bi-dimensional.
Ejemplo: Integración gaussiana en dos dimensiones
La integral gaussiana en 2 dimensiones es
donde  es una matriz simétrica bi-dimensional definida como
es una matriz simétrica bi-dimensional definida como
 es una matriz simétrica bi-dimensional definida como
es una matriz simétrica bi-dimensional definida como
y donde hemos usado el convenio de sumación de Einstein.
Diagonalización de la matriz
El primer paso es diagonalizar la matriz.3 Nótese que
donde, como  es una matriz simétrica real, podemos elegir una matriz ortogonal(y por tanto también unitaria)
es una matriz simétrica real, podemos elegir una matriz ortogonal(y por tanto también unitaria)  .
.
 es una matriz simétrica real, podemos elegir una matriz ortogonal(y por tanto también unitaria)
es una matriz simétrica real, podemos elegir una matriz ortogonal(y por tanto también unitaria)  .
.
Elegimos la matriz  de tal manera que
de tal manera que
 de tal manera que
de tal manera que
sea diagonal.
Autovalores de A
Los autovalores de  son las soluciones de su polinomio característico
son las soluciones de su polinomio característico
 son las soluciones de su polinomio característico
son las soluciones de su polinomio característico
que son
Autovectores de A
Sustituyendo los autovalores otra vez en la ecuación que define los autovectores, tenemos
o
De la ecuación característica tenemos que
Nótese también que
Los autovectores pueden ser escritos como
y
Aquí, 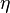 es una constante de normalización dada por
es una constante de normalización dada por
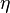 es una constante de normalización dada por
es una constante de normalización dada por
Es fácil verificar que los 2 autovectores son ortogonales entre sí.
Construcción de la matriz ortogonal
La matriz ortogonal  se construye usando los autovectores normalizados de la matriz
se construye usando los autovectores normalizados de la matriz  como columnas de la matriz ortogonal.
como columnas de la matriz ortogonal.
 se construye usando los autovectores normalizados de la matriz
se construye usando los autovectores normalizados de la matriz  como columnas de la matriz ortogonal.
como columnas de la matriz ortogonal.
Nótese que el determinante de  , al ser una matriz unitaria, es igual a uno.
, al ser una matriz unitaria, es igual a uno.
 , al ser una matriz unitaria, es igual a uno.
, al ser una matriz unitaria, es igual a uno.
Si definimos
entonces, la matriz ortogonal puede escribirse como
lo que representa una rotación de los autovectores.
La inversa de esta matriz es
Matriz diagonal
La matriz diagonal es
con autovectores
y
Ejemplo numérico
Los autovalores son
Los autovectores son
y
donde
 .
.
La matriz ortogonal es
Es fácil comprobar que el determinante de  es 1.
es 1.
 es 1.
es 1.
La matriz inversa de  es
es
 es
es
Por lo que la matriz diagonal  es
es
 es
es
con autovectores
y
Reescalado de las variables e integración
Tras la diagonalización, la integral a resolver se puede escribir como
donde
 .
.
Como la transformación de coordenadas aplicada es una rotación, el determinante jacobiano de la transformación es igual a la unidad, por lo que
 .
.
Con lo que ya podemos resolver la integral
que es la solución buscada.
Integrales con términos complejos lineales en varias dimensiones
Una vez que tenemos resuelto el ejemplo bi-dimensional, es fácil generalizar el resultado obtenido al plano complejo y a varias dimensiones.
Integrales con un término lineal real en el argumento
Integrales con un término lineal imaginario en el argumento
Integrales con un término complejo cuadrático
Integrales con operadores diferenciales en el argumento
Por ejemplo, véase la integral4
donde 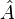 es un operador diferencial con
es un operador diferencial con  y
y  funciones definidas en el espacio-tiempo.
funciones definidas en el espacio-tiempo.  representa una integración sobre todos los posibles caminos. Análogamente a la versión matricial de esta integral, la solución es
representa una integración sobre todos los posibles caminos. Análogamente a la versión matricial de esta integral, la solución es
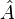 es un operador diferencial con
es un operador diferencial con  y
y  funciones definidas en el espacio-tiempo.
funciones definidas en el espacio-tiempo.  representa una integración sobre todos los posibles caminos. Análogamente a la versión matricial de esta integral, la solución es
representa una integración sobre todos los posibles caminos. Análogamente a la versión matricial de esta integral, la solución es
donde
Análogamente se obtienen los siguientes resultados
![\int \exp\left[ i \int d^4x \left ( \frac 1 2 \varphi \hat A \varphi + J \varphi \right) \right ] D\varphi \; \propto \;
\exp \left( { i\over 2} \int d^4x \; d^4y J\left ( x \right ) D\left ( x - y \right ) J\left( y \right ) \right)](https://upload.wikimedia.org/math/d/0/7/d07a792846126656cc2834732b58f5d2.png) .
.
Integrals that can be approximated by the method of steepest descent
En teoría cuántoca de campos, es muy usual encontrarse con integrales n-dimensionales de la forma
 es la constante de Planck reducida y
es la constante de Planck reducida y  es una función con un mínimo positivo en
es una función con un mínimo positivo en  . Estas integrales pueden aproximarse por el método del descenso más brusco.
. Estas integrales pueden aproximarse por el método del descenso más brusco.
Asumiendo que la constante de Planck es suficientemente pequeña, la función  puede aproximarse por su serie de Taylor alrededor de su mínimo
puede aproximarse por su serie de Taylor alrededor de su mínimo
 puede aproximarse por su serie de Taylor alrededor de su mínimo
puede aproximarse por su serie de Taylor alrededor de su mínimo![\int_{-\infty}^{\infty} \exp\left[ -{1 \over \hbar} \left( f\left( q_0 \right) + {1\over 2} \left( q-q_0\right)^2f^{\prime \prime} \left( q-q_0\right) + \cdots \right ) \right] d^nq](https://upload.wikimedia.org/math/b/7/f/b7f96b6c676e0430b6e08507ca19e91e.png) .
.
Aquí,  es la matriz Hessiana de
es la matriz Hessiana de  en
en  , es decir, una matriz
, es decir, una matriz 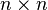 de segundas derivadas parciales evaluadas en el mínimo de la función.
de segundas derivadas parciales evaluadas en el mínimo de la función.
 es la matriz Hessiana de
es la matriz Hessiana de  en
en  , es decir, una matriz
, es decir, una matriz 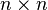 de segundas derivadas parciales evaluadas en el mínimo de la función.
de segundas derivadas parciales evaluadas en el mínimo de la función.
Si despreciamos mayores órdenes de la expansión de la serie de Taylor, podemos resolver la integral explícitamente.
![\int_{-\infty}^{\infty} \exp\left[ -{1 \over \hbar} \left( f\left( q \right) \right ) \right] d^nq \approx
\exp\left[ -{1 \over \hbar} \left( f\left( q_0 \right) \right ) \right] \sqrt{ (2 \pi \hbar )^n \over \det f^{\prime \prime} }](https://upload.wikimedia.org/math/0/2/5/0254891ceab1b892b1c7b32b82c1a471.png) .
.
Integrales que pueden ser aproximadas por el método de la fase estacionaria
Otra integral común es la integral de caminos de la forma
donde  es la acción clásica y el dominio de integración son todos los posibles caminos que una partícula podría tomar. En el límite de
es la acción clásica y el dominio de integración son todos los posibles caminos que una partícula podría tomar. En el límite de  pequeña, la integral puede aproximarse por el método de la fase estacionaria. En esta aproximación, la integral queda definida solamente sobre el camino en el cuál la acción es un punto estacionario (un mínimo, un máximo o un punto de silla). Por tanto, a través de esta aproximación se recupera la mecánica clásica como el límite clásico de la mecánica cuántica.
pequeña, la integral puede aproximarse por el método de la fase estacionaria. En esta aproximación, la integral queda definida solamente sobre el camino en el cuál la acción es un punto estacionario (un mínimo, un máximo o un punto de silla). Por tanto, a través de esta aproximación se recupera la mecánica clásica como el límite clásico de la mecánica cuántica.
 es la acción clásica y el dominio de integración son todos los posibles caminos que una partícula podría tomar. En el límite de
es la acción clásica y el dominio de integración son todos los posibles caminos que una partícula podría tomar. En el límite de  pequeña, la integral puede aproximarse por el método de la fase estacionaria. En esta aproximación, la integral queda definida solamente sobre el camino en el cuál la acción es un punto estacionario (un mínimo, un máximo o un punto de silla). Por tanto, a través de esta aproximación se recupera la mecánica clásica como el límite clásico de la mecánica cuántica.
pequeña, la integral puede aproximarse por el método de la fase estacionaria. En esta aproximación, la integral queda definida solamente sobre el camino en el cuál la acción es un punto estacionario (un mínimo, un máximo o un punto de silla). Por tanto, a través de esta aproximación se recupera la mecánica clásica como el límite clásico de la mecánica cuántica.Integrales de Fourier
Función delta de Dirac
La función delta de Dirac puede representarse de la siguiente manera como la siguiente transformada de Fourier5
 .
.
En el caso  dimensional tenemos la generalización inmediata
dimensional tenemos la generalización inmediata
 dimensional tenemos la generalización inmediata
dimensional tenemos la generalización inmediata .
.
Integrales de Fourier de generalizaciones del potencial de Coulomb
Laplaciano de 1/r
Aplicando el teorema de Gauss se tiene que, en el espacio tridimensional
donde
Esta indentidad se puede usar para derivar igualdades entre integrales. Por ejemplo, véase la descomposición en campos longitudinal y transversal.
A partir de la igualdad de arriba, se obtiene inmediatamente que la representación de 1/r como integral de Fourier es
Potencial de Yukawa: El potencial de Coulomb con masa
El potencial de Yukawa en 3 dimensiones puede representarse como una integral de su transformada de Fourier6
donde
y
En el límite de masa  pequeña, esta inteegral se reduce a
pequeña, esta inteegral se reduce a
 pequeña, esta inteegral se reduce a
pequeña, esta inteegral se reduce a .
.
Para obtener este límite de la forma correcta, nótese que:
Potencial de Coulomb modificado con masa
donde el gorro indica que el vector es de módulo unidad en el espacio tridimensional.
En el límite de masa  pequeña, esta integral se anula.
pequeña, esta integral se anula.
 pequeña, esta integral se anula.
pequeña, esta integral se anula.
Para obtener este límite de la forma correcta, nótese que:
donde
Nótese que, en este límite, cuando
por lo que el lado derecho de la igualdad es proporcional a  , que en este límite es cero.
, que en este límite es cero.
 , que en este límite es cero.
, que en este límite es cero.Potencial longitudinal con masa
donde el gorro indica que el vector es de módulo unidad en el espacio tridimensional.
En el límite de masa  pequeña, esta integral se aproxima a
pequeña, esta integral se aproxima a
 pequeña, esta integral se aproxima a
pequeña, esta integral se aproxima a
La integral se resuelve en coordenadas esféricas:
Usando los resultados anteriores, se obtiene
![=
{1\over 2} {e^{ - m r } \over 4 \pi r } \left[ \mathbf 1 - \mathbf{\hat r} \mathbf{\hat r} \right]
+
{e^{ - m r } \over 4 \pi r } \left\{ 1+ {2\over mr }
- {2\over \left(mr\right)^2 } \left( e^{mr} -1 \right) \right \}
\left\{ {1\over 2} \left[\mathbf 1 + \mathbf{\hat r} \mathbf{\hat r}\right] \right\}](https://upload.wikimedia.org/math/3/c/e/3ce3b09d61e5881ecdcf45ce0774079d.png) .
.
Potencial transversal con masa
En el límite de  pequeño, esta integral se aproxima a
pequeño, esta integral se aproxima a
 pequeño, esta integral se aproxima a
pequeño, esta integral se aproxima a
Para grandes distancias, la integral decae cúbicamente con 

Integración angular en coordenadas cilíndricas
La integración angular de una exponencial en coordenadas cilíndricas se puede escribir en función de funciones de Bessel de primer tipo7 8
Funciones de Bessel
Integración del propagador del campo con masa en coordenadas cilíndricas
Función de Bessel lineal
Véase Abramowitz and Stegun.9
Para  , tenemos10
, tenemos10
 , tenemos10
, tenemos10
donde  es la constante de Euler-Mascheroni.
es la constante de Euler-Mascheroni.
 es la constante de Euler-Mascheroni.
es la constante de Euler-Mascheroni.Cuadrado de funciones de Bessel
Véase11
Para  la integral se reduce a
la integral se reduce a
 la integral se reduce a
la integral se reduce a
mientras que para  se tiene
se tiene
 se tiene
se tiene
En general
Integración de una función de onda magnética
La integral bi-dimensional sobre una función de onda magnética es12
donde  es una función hipergeométrica confluente.
es una función hipergeométrica confluente.
 es una función hipergeométrica confluente.
es una función hipergeométrica confluente.Matrices de Pauli
matrices de Pauli, deben su nombre a Wolfgang Ernst Pauli, son matrices usadas en física cuántica en el contexto del momento angular intrínseco o espín. Matemáticamente, las matrices de Pauli constituyen una base vectorial del álgebra de Lie del grupo especial unitario SU(2), actuando sobre la representación de dimensión 2.
Forma de las matrices
Cumplen las reglas de conmutación del álgebra de Lie  :
:
 :
:
Donde:
 es el Símbolo de Levi-Civita (pseudotensor totalmente antisimétrico).
es el Símbolo de Levi-Civita (pseudotensor totalmente antisimétrico).
También satisfacen la siguiente regla de anticonmutación
Otras propiedades importantes son:
Caso de espín 1/2
Las matrices de Pauli son tres, al igual que la dimensión del álgebra del Lie del grupo SU(2). En su representación lineal más común tienen la siguiente forma:
Caso de espín 1
Por abuso de lenguaje se suele llamar matrices de Pauli a otras representaciones lineales diferentes a las usadas en el caso de espín 1/2 anterior. Por ejemplo para representar el espín de una partícula con valor 1, se usa la representación lineal mediante matrices de 3x3 siguiente:
Caso de espín 3/2
Análogamente al caso anterior para espín 3/2 es común usar la siguiente representación:
Aplicaciones
Las matrices de Pauli tienen gran utilidad en mecánica cuántica. La aplicación más conocida es la representación del operador de espín para una partícula de espín 1/2, como un electrón, un neutrón o un protón. Así el observable que sirve para medir al espín, o momento angular intrínseco, de un electrón, en la dirección i, viene dado por el operador autoadjunto:
En la representación convencional, los autoestados de espín corresponden a los vectores:


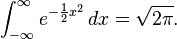







![\begin{align}
& \int_{-\infty}^\infty \exp\left( -{1 \over 2} a x^2 + Jx\right) \, dx = \exp\left( { J^2 \over 2a } \right ) \int_{-\infty}^\infty \exp \left [ -{1 \over 2} a \left ( x - { J \over a } \right )^2 \right ] \, dx \\[8pt]
& = \exp\left( { J^2 \over 2a } \right )\int_{-\infty}^\infty \exp\left( -{1 \over 2} a x^2 \right) \, dx = \left ( {2\pi \over a } \right ) ^{1\over 2} \exp\left( { J^2 \over 2a }\right )
\end{align}](https://upload.wikimedia.org/math/6/3/3/633fa2674ad6f992e1936e3859a8b15d.png)
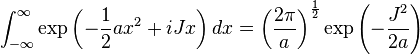






![A = \bigl[ \begin{smallmatrix}
a&c\\ c&b
\end{smallmatrix} \bigr]](https://upload.wikimedia.org/math/f/8/8/f8847673fbb98989bdf3a9ff981190a3.png)
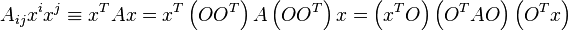

 de
de ![\bigl[ \begin{smallmatrix}
a&c\\ c&b
\end{smallmatrix} \bigr]
\bigl[ \begin{smallmatrix}
u\\ v
\end{smallmatrix} \bigr] =
\lambda \bigl[ \begin{smallmatrix}
u\\ v
\end{smallmatrix} \bigr].](https://upload.wikimedia.org/math/1/f/2/1f2d27781b01591087dbd5b6ee80ed5d.png)




























![\int \exp\left[ \int d^4x \left ( -\frac 1 2 \varphi \hat A \varphi + J \varphi \right) \right ] D\varphi](https://upload.wikimedia.org/math/e/0/b/e0b176578d63600fbf6304ad21dab972.png)


 , es el
, es el  es la
es la ![\int \exp\left[ \int d^4x \left ( -\frac 1 2 \varphi \hat A \varphi + i J \varphi \right) \right ] D\varphi \; \propto \;
\exp \left( - { 1\over 2} \int d^4x \; d^4y J\left ( x \right ) D\left ( x - y \right ) J\left( y \right ) \right)](https://upload.wikimedia.org/math/5/b/d/5bda247086c31a7c69e12505a239f788.png)

















![\int { d^3 k \over \left ( 2 \pi \right ) ^3 }
\; \mathbf{\hat{k}} \mathbf{\hat{k}} \;
{ \exp \left ( i\mathbf{k} \cdot \mathbf{r} \right ) \over k^2 +m^2 }
=
{1\over 2} {e^{ - m r } \over 4 \pi r } \left[ \mathbf{1}- \mathbf{\hat{r}} \mathbf{\hat{r}} \right]
+
{1\over 2} {e^{ - m r } \over 4 \pi r } \left\{ 1+ {2\over mr}
- {2 \over \left( mr \right)^2 } \left( e^{mr} -1 \right) \right \}
\left[\mathbf{1}+ \mathbf{\hat{r}} \mathbf{\hat{r}}\right]](https://upload.wikimedia.org/math/b/f/1/bf1a2b322f384dbcfc9a2d30bfe3d746.png)
![{1\over 2} {1 \over 4 \pi r } \left[ \mathbf 1 - \mathbf{\hat r} \mathbf{\hat r} \right] .](https://upload.wikimedia.org/math/c/c/3/cc34b19f46af87b586fa1b8273ab8694.png)
![\int { d^3 k \over \left ( 2 \pi \right ) ^3 } \mathbf{\hat k} \mathbf{\hat k}
{ \exp \left ( i\mathbf k \cdot \mathbf r \right ) \over k^2 +m^2 }
=
\int { d^3 k \over \left ( 2 \pi \right ) ^3 }
\left[
\left( \mathbf{\hat k}\cdot \mathbf{\hat r}\right)^2\mathbf{\hat r} \mathbf{\hat r}
+ \left( \mathbf{\hat k}\cdot \mathbf{\hat \theta}\right)^2\mathbf{\hat \theta} \mathbf{\hat \theta}
+ \left( \mathbf{\hat k}\cdot \mathbf{\hat \phi}\right)^2\mathbf{\hat \phi} \mathbf{\hat \phi}
\right]
{ \exp \left ( i\mathbf k \cdot \mathbf r \right ) \over k^2 +m^2 }](https://upload.wikimedia.org/math/e/b/8/eb8eec0a96a68f5dfc2bcde6776a4981.png)
![=
{1 \over 4 \pi r } \exp \left ( - m r \right ) \left\{ 1+ {2\over mr }
- {2\over \left(mr\right)^2 } \left( e^{mr} -1 \right) \right \}
\left\{\mathbf 1 - {1\over 2} \left[\mathbf 1 - \mathbf{\hat r} \mathbf{\hat r}\right] \right\}
+
\int_0^{\infty} {k^2 dk \over \left ( 2 \pi \right )^2 } \int_{-1}^{1} du {\exp\left( ikru \right) \over k^2 + m^2}
{1\over 2} \left[ \mathbf 1 - \mathbf{\hat r} \mathbf{\hat r} \right]](https://upload.wikimedia.org/math/8/0/7/80767ce06f72d88b3bf3f5f0853c8074.png)
![\int { d^3 k \over \left ( 2 \pi \right ) ^3 }
\; \left[ \mathbf{1} - \mathbf{\hat{k}} \mathbf{\hat{k}} \right] \;
{ \exp \left ( i \mathbf{k} \cdot \mathbf{r}\right ) \over k^2 +m^2 }
= {1\over 2} {e^{ - m r } \over 4 \pi r } \left\{
{2 \over \left( mr \right)^2 } \left( e^{mr} -1 \right) - {2\over mr} \right \}
\left[\mathbf{1} + \mathbf{\hat{r}} \mathbf{\hat{r}}\right]](https://upload.wikimedia.org/math/e/3/2/e32b6f15d2a529c8d69b937a9969669b.png)
![{1\over 2} {1 \over 4 \pi r }
\left[\mathbf 1 + \mathbf{\hat r} \mathbf{\hat r}\right]
.](https://upload.wikimedia.org/math/5/7/8/578090559934178a1905b197c44f31e7.png)
![{1\over 4 \pi m^2r^3 }
\left[\mathbf 1 + \mathbf{\hat r} \mathbf{\hat r}\right]
.](https://upload.wikimedia.org/math/d/e/3/de349c2e190e1f31bbd1e303fa124530.png)





![\int_o^{\infty} {k\; dk \over k^2 +m^2} J_1^2 \left( kr \right)
\rightarrow
{1\over 2 }\left[ 1 - {1\over 8} \left(mr\right)^2 \right],](https://upload.wikimedia.org/math/6/6/5/665b76fb692dbb7f67a5d560c935a32c.png)



![\left [\sigma_i,\sigma_j \right ]=2i\ \epsilon_{ijk}\ \sigma_k](https://upload.wikimedia.org/math/f/6/a/f6aa088e46878a34792ec106bc5d4577.png)









No hay comentarios:
Publicar un comentario