Análisis de circuitos en ingeniería

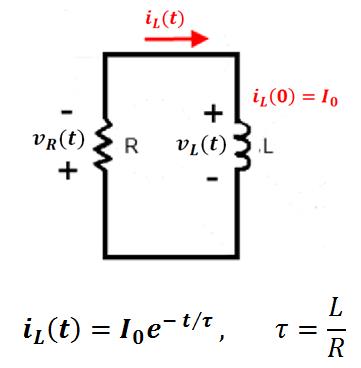
Propiedades de la respuesta exponencial en un circuito RL

La relación L/R representa el “ancho” de la curva y se denomina constante de tiempo o tau, y sus unidades son los segundos.

Ahora vamos a analizar un poco el tao:

• En t=0 la corriente tiene un valor inicial.
• Conforme la transcurre el tiempo, la corriente disminuye y tiende a cero.
• La corriente tiene una forma exponencial decreciente.
• El tiempo t= L/R es el tiempo que emplearía la corriente en caer hasta cero si continuase cayendo a la rapidez inicial de decaimiento, m0.
• La curva cambia solo si cambia la constante de tiempo, por lo cual para cualquier circuito que tenga la misma constante tau, tendrá la misma curva.
• Si se duplica el tau la respuesta original ocurrirá en un tiempo posterior, y la nueva curva se obtiene colocando cada punto de la curva original dos veces más lejano hacia la derecha.
• Con un tau más grande, la corriente tardará más en decaer a cualquier fracción dada de su valor original.
• El “ancho” de la curva es proporcional a L/R.
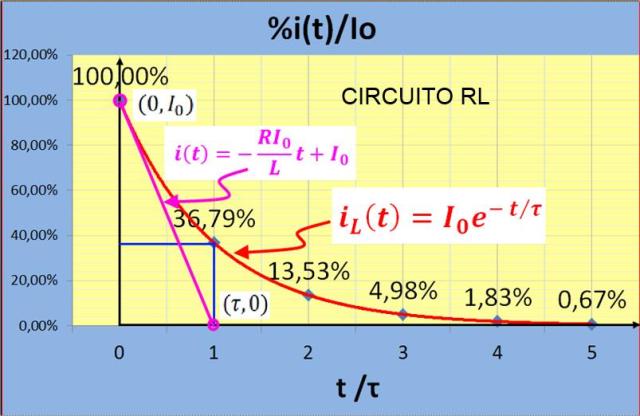
• En t= 1 tau, i (t) = 36,79%Io
• Se considera que el tiempo que toma la corriente en caer a cero (tiempo de descarga) es de alrededor de 5 constantes de tiempo o 5 tau. En este tiempo la corriente ha caído a menos del 1% de la corriente inicial.

• Ejemplo 1 Constante de tiempo

En un circuito RL serie calcule la razón i (2T)/i (0)

• Ejemplo 2 Constante de tiempo

En un circuito RL serie calcule la razón i (4T)/i (2T)

• Ejemplo 3. Constante de tiempo

En un circuito RL serie calcule la razón t/T si i (t) =0,1 i (T)

• Ejemplo 4. Constante de tiempo

En un circuito RL serie calcule la razón t/T si i (t) – i (T) =0,1 i (0)

Evaluación de la constante de tiempo en forma gráfica

La constante de tiempo de un circuito RL serie se puede evaluar en forma gráfica a partir de la curva de respuesta i (t).

Solo se necesita dibujar la recta tangente a i (t) en t=0, y determinar la intersección de esta línea tangente en el eje del tiempo.

A menudo esta es una forma conveniente de calcular el valor aproximado de la constante de tiempo en la pantalla de un osciloscopio.

Como en t= 1 tau, i (t) = 37%Io, se localiza este valor en forma aproximada en el eje de corriente en la pantalla del osciloscopio y desde allí se traza una horizontal que corte la gráfica de i(t). Por este punto de intersección de traza una vertical hasta el eje del tiempo, y así se obtiene el tau o constante de tiempo en forma aproximada.

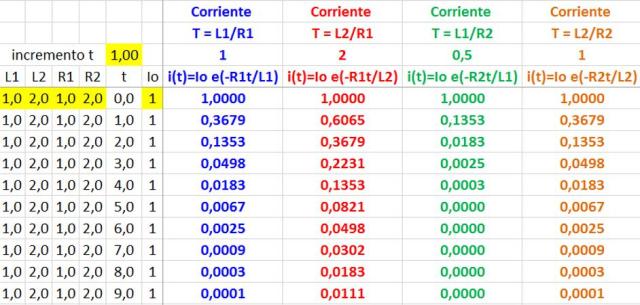
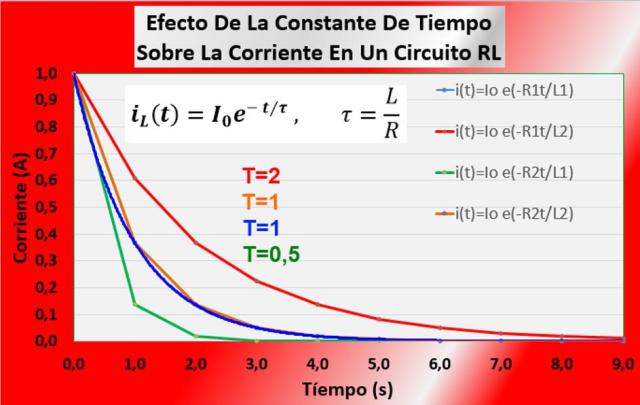
Efecto de la constante de tiempo sobre la corriente en un circuito RL

1. Un aumento de la constante de tiempo produce un mayor tiempo de descarga, o una respuesta que decae más lentamente.
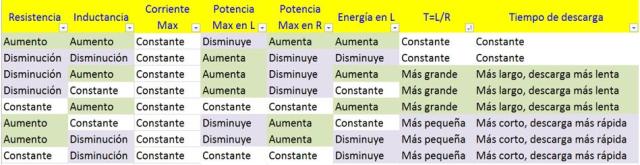
2. Se logran constantes de tiempo más grandes, y por tanto, tiempos de descarga más lentos si se aumenta la inductancia y/o disminuye la resistencia, y constantes de tiempo más pequeñas y por tanto tiempos de descarga más rápidos si se disminuye la inductancia y/o aumenta la resistencia.
3. El tao y el tiempo de descarga se mantendrán constantes siempre que la resistencia y la inductancia varíen en forma proporcional por el mismo factor.
4. Una disminución de la resistencia o aumento de la inductancia produce un corrimiento de la gráfica a la derecha, es decir se aumenta el tao o ancho del voltaje.

Efecto de la constante de tiempo sobre la potencia del resistor y la bobina en un circuito RL

1. Se puede aumentar el tao L/R disminuyendo el valor de R.
2. Si se disminuye R la potencia transferida al resistor es menor para la misma corriente inicial.
3. Si se mantiene constante la resistencia, la potencia del resistor y de la bobina se mantiene constante.

1. Un aumento de la resistencia está asociado con la disminución de la potencia en la bobina, y el aumento de la potencia en el resistor.
2. La potencia del resistor y del inductor se mantendrá constante siempre que no varíe la resistencia.