El Circuito RL simple: un resistor y un inductor
Forma de solución 1: suponer una respuesta para la ecuación diferencial
Paso 1: suponer una respuesta
Constantes desconocidas: A y S1
Paso 2: derivar la respuesta
Paso 3: Sustituir la respuesta y la derivada en la ecuación diferencial
Paso 4: factorizar
Paso 5: analizar los tres factores que hacen cero la ecuación.
La relación L/R representa el “ancho” de la curva y se denomina constante de tiempoo tau, y sus unidades son los segundos y las unidades de S1 corresponden a una frecuencia. Veámoslo:
Paso 6: calcular la amplitud A.
Se hace uso de la condición inicial:
Paso 7: obtener la respuesta: corriente en la bobina y en el resistor.
La corriente a través del resistor es la misma que en la bobina por estar en serie.
Paso 8: verificar la respuesta.
Sustituir la respuesta en la ecuación diferencial y obtener una identidad 0=0. Además, se sustituye t=0 en la respuesta, para obtener la condición inicial.
Paso 9: obtener la potencia DISIPADA en el resistor.
La corriente a través del resistor es la misma que la de la bobina por estar en serie.
Paso 10: obtener la potencia GENERADA en el inductor
Observe que la suma de potencias generada y consumida es cero.
Paso 11: obtener la energía convertida en calor en el resistor en un tiempo t
La energía TOTAL convertida en calor en el resistor se calcula integrando la potencia instantánea desde un tiempo CERO hasta un tiempo INFINITO.
Paso 12: obtener la energía ALMACENADA en el inductor
Observaciones:
La suma de potencia generada y consumida es cero.
La bobina se comporta como una fuente durante un tiempo t
La energía total disipada en el resistor es la misma que la energía total almacenada en el inductor.
La energía almacenada en el inductor se disipa con el tiempo a través del resistor. Por esto hay que tener cuidado de verificar que las bobinas estén descargadas antes de manipularlas.
La energía almacenada en el inductor en t=0 es cero, a menos que se tenga alguna energía almacenada previamente.
Forma de solución 2: resolver la ecuación diferencial
Casi nunca es posible separar variables, por lo que es más conveniente y poderososuponer una respuesta, donde haya varias constantes desconocidas, y obtener estas constantes tal que satisfagan la ecuación diferencial y las condiciones iniciales.
En análisis de circuitos es común encontrar ecuaciones diferenciales cuya respuesta corresponde a una función exponencial o a la suma de varias funciones exponenciales.
Ejemplo 1. Circuito RL simple
Solución:
Método de solución paso a paso de un circuito RL
Respuesta Natural
- Paso 4: calcular Req y Leq
- Paso 5: Calcular la frecuencia y la constante de tiempo.
- Paso 6: Calcular la amplitud a partir de la condición inicial.
- Paso 7: Hallar las demás respuestas.
Ejemplo 1: Eliminación súbita de fuentes. Respuesta Natural. Circuito RL
Caso 1: un resistor y un inductor.
La identificación del caso se hace justo después de haber eliminado o desconectado la fuente, no antes.
El circuito siguiente ha estado en la condición mostrada un tiempo muy largo. El interruptor se abre cuando t = 0.
Solución:
Paso 1: Determinar el circuito en t < 0 y calcular iL(0-)
En t < 0 el suiche Sw1 está cerrado. La bobina se comporta como un corto circuito en C.C.
A su vez, R1 está en corto a través de la bobina, y R2 está en corto a través de la bobina y el interruptor
Paso 2: Determinar el circuito en t > 0 y calcular iL (0+)
En t > 0 el interruptor Sw1 está abierto. Hay una desconexión súbita de la fuente.
Como la corriente no puede cambiar bruscamente en una bobina:
Paso 3: escribir la forma funcional de la respuesta
En este punto se identifica el caso, pues ya la fuente ha sido desconectada del circuito que involucra a la bobina.Observe que quedan dos circuitos separados.
Caso 1: un resistor y un inductor.
Paso 4: calcular Req y Leq
En este caso solo hay un resistor para la descarga. La bobina se descargará a través del resistor R1 en t=0+.
Paso 5: Calcular la frecuencia y la constante de tiempo.
Paso 6: Calcular la amplitud a partir de la condición inicial.
Paso 7: Hallar las demás respuestas.
Ejemplo 2: Eliminación súbita de fuentes. Respuesta Natural.Circ uito RL
Caso 1: un resistor y un inductor.
El circuito siguiente ha estado en la condición mostrada un tiempo muy largo. El interruptor se abre cuando t = 0. El interruptor es un interruptor de un polo y dos tiros que se ha dibujado para indicar que cierra un circuito antes de abrir el otro. Se le conoce como hacer antes de cortar.
Solución
Paso 1: Determinar el circuito en t < 0 y calcular iL (0- )
El suiche Sw está en cerrado en A. La bobina se comporta como un corto circuito en C.C. R2 no existe en t=0- ya que no circula corriente por él.
Paso 2: Determinar el circuito en t > 0 y calcular iL(0+)
En la posición intermedia entre A y B el resistor R2 está en corto y la corriente circula por la malla externa naranja. La bobina continúa en presencia de la fuente de C.C.
En t=0+ el suiche Sw1 está en la posición B. Se ha desconectado la fuente súbitamente. Como la corriente no puede cambiar bruscamente en una bobina:
Paso 3: escribir la forma funcional de la respuesta
Caso 1: un resistor y un inductor.
Paso 4: calcular Req y Leq
La bobina se descargará a través del resistor R2 en t=0+.
Paso 5: Calcular la frecuencia y la constante de tiempo.
Paso 6: Calcular la amplitud a partir de la condición inicial I0.
Paso 7: Hallar las demás respuestas.
Ejemplo 3: Eliminación súbita de fuentes. Respuesta Natural. Circuito RL
Caso 2: varios resistores y un inductor.
El circuito siguiente ha estado en la condición mostrada un tiempo muy largo. El interruptor se abre cuando t = 0.
Solución
Paso 1: Determinar el circuito en t<0 calcular="" il="" span="" y="">
El suiche Sw1 está cerrado.
La bobina se comporta como un corto circuito en C.C.
La corriente por la bobina se conocerá cuando se tenga el voltaje en el nodo V.
LCK en nodo V: suma de corrientes que salen igual a cero.
Paso 2: Determinar el circuito en t>0 y calcular iL (0+)
El suiche Sw1 está abierto.
Como la corriente no puede cambiar bruscamente en una bobina:
Paso 3: escribir la forma funcional de la respuesta.
Caso 2: varios resistores y un inductor.
Paso 4: calcular Req y Leq
La bobina se descargará a través de los resistores R2 y R3 del circuito en t=0+.
Paso 5: Calcular la frecuencia y la constante de tiempo.
Paso 6: Calcular la amplitud a partir de la condición inicial.
Paso 7: Hallar las demás respuestas.
Ejemplo 4: Eliminación súbita de fuentes. Respuesta Natural. Circuito RL
Caso 2: varios resistores y un inductor.
Conocida la corriente inicial por la bobina.
Solución
Paso 1: Determinar el circuito en t<0 calcular="" il="" span="" y="">
Paso 2: Determinar el circuito en t>0 y calcular iL (0+)
Paso 2: Determinar el circuito en t>0 y calcular iL (0+)
Como la corriente no puede cambiar bruscamente en una bobina:
Paso 3: escribir la forma funcional de la respuesta.
Paso 3: escribir la forma funcional de la respuesta.
Caso 2: varios resistores y un inductor.
Paso 4: calcular Req y Leq
Paso 4: calcular Req y Leq
La bobina se descargará a través de todos los resistores del circuito R1, R2, R3 y R4 en t=0+.
Paso 6: Calcular la amplitud a partir de la condición inicial.
Paso 7: Hallar las demás respuestas.
Ejemplo 5: Eliminación súbita de fuentes. Respuesta Natural. Circuito RL
Caso 2: varios resistores y un inductor.
Conocida la corriente inicial por R1, y no la del inductor.
Solución
Paso 1: Determinar el circuito en t < 0 y calcular iL(0-)
Paso 2: Determinar el circuito en t > 0 y calcular iL(0+)
Como la corriente no puede cambiar bruscamente en una bobina:
Paso 3: escribir la forma funcional de la respuesta.
Caso 2: varios resistores y un inductor.
Paso 4: calcular Req y Leq
La bobina se descargará a través de todos los resistores R1, R2, R3 y R4 del circuito en t=0+.
Paso 5: Calcular la frecuencia y la constante de tiempo.
Paso 6: Calcular la amplitud a partir de la condición inicial
Paso 7: Hallar las demás respuestas.
Ejemplo 6: Eliminación súbita de fuentes. Respuesta Natural. Circuito RL
Caso 2 varios resistores y un inductor
Solución
Paso 1: Determinar el circuito en t<0 calcular="" il1="" nbsp="" span="" y="">
El suiche Sw está abierto. La bobina se comporta como un corto circuito en C.C. Las corrientes son constantes y no exponenciales.
Paso 2: Determinar el circuito en t>0 y calcular iL1 (0+)
El suiche Sw está cerrado. La fuente está en corto. Se ha desconectado la fuente súbitamente. Como la corriente no puede cambiar bruscamente en una bobina:
Paso 3: escribir la forma funcional de la respuesta.
Caso 2: varios resistores y un inductor.
Paso 4: calcular Req y Leq
Paso 5: Calcular la frecuencia y la constante de tiempo.
Paso 6: Calcular la amplitud a partir de la condición inicial I0.
Paso 7: Hallar las demás respuestas.
Ejemplo 7: Eliminación súbita de fuentes. Respuesta Natural. Circuito RL
Caso 4: varios resistores y varios inductores.
Solución
Paso 1: Determinar el circuito en t<0 calcular="" il1="" span="" y="">
El suiche Sw está cerrado. La bobina se comporta como un corto circuito en C.C. Las corrientes son constantes y no exponenciales en t<0 .="" p="">
Paso 2: Determinar el circuito en t>0 y calcular iL1 (0+)
El suiche Sw está abierto. Se ha desconectado la fuente súbitamente. Como la corriente no puede cambiar bruscamente en una bobina:
Paso 3: escribir la forma funcional de la respuesta.
Caso 2: varios resistores y varios inductores.
Paso 4: calcular Req y Leq
Paso 5: Calcular la frecuencia y la constante de tiempo.
Paso 6: Calcular la amplitud a partir de la condición inicial
Paso 7: Hallar las demás respuestas.
analisisdecircuitos1.wordpress.com
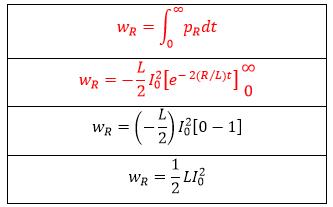
No hay comentarios:
Publicar un comentario