Apuntes de cálculo

Cálculo diferencial

La aplicación progrediente o pushforward es una aplicación asociada a una aplicación entre variedades diferenciables, que permite asociar campos tensoriales definidos sobre la primera variedad con campos definidos sobre la segunda.

Supóngase que φ : M → N es una aplicación diferenciable entre variedades diferenciables; entonces la[aplicación] diferencial de φ en un punto x es, en un cierto sentido, la mejor aproximación lineal de φaldededor del punto x. Es decir, generaliza el concepto de derivada o matriz jacobiana de una función de nvariables del cálculo ordinario. Explícimente es una aplicación lineal que va desde el espacio tangente a Men el punto x al espacio tangente a N en el punto φ(x). De ahí, que se use el término push 'empujar' en inglés o progrediente (del latín prōgrediens 'que avanza hacia delante') ya que "lleva hacia delante" vectores de Mhasta superponerlos con vectores de N.

La diferencial diferancial (también llamada aplicación tangente) asociada a una aplicación φ también es llamada simplemente derivada o derivada total de φ, y a veces se llama incluso pushforward.

Si una aplicación, φ, aplica cada punto de una variedad diferenciable M a un punto de una variedad N, entonces elpushforward de φ aplica vectores del espacio tangente en cada punto de M a vectores del espacio tangente a cada punto de N.

Motivación

Sea φ:U→V una aplicación diferenciable desde un conjunto abierto U de R^m hasta un conjunto abierto V de Rⁿ. Para cualquier punto x de U, la matriz jacobiana de φ en el punto x (con respecto a las coordinadas estándar) de hecho resulta ser la matriz de componentes de la aplicación diferencial asociada a φ en el punto x, que naturalmente es una aplicación lineal:

de R^m a Rⁿ.

La aplicación progrediente pretende generalizar esto al caso en que φ sea una aplicación continua entre dos variedades diferenciales cualquiera M y N. Además la aplicación progrediente puede generalizarse a objetos tensoriales definidos sobre el espacio tangente a una variedad.

Diferencial de una aplicación difenciable

Sea φ: M → N una aplicación lineal entre variedades diferenciables. Dado un cierto x ∈ M, la differential de φ en el punto x es una aplicación lineal:

definida en el espacio tangente de M en el punto x al espacio tangente de N en el punto φ(x). La aplicación dφ_x del espacio vectorial tangente X se llama aplicación progrediente o pushforward de X por φ. La definición exacta de esta aplicación progrediente depende de la definición que uno use para los vectores tangentes.

Por ejemplo, si los vectores tangentes en un punto x se definen como clases de equivalencia de las curvas que pasan a través de x entonces la aplicación diferencial viene dada por:

donde γ es una curva sobre M que cumple que γ(0) = x. En otras palabras, la aplicación progrediente del vector tangente a la curva γ en 0 es precisamente el vector tangente a la curva φ∘γ en 0.

Por otra parte, si los vectores tangentes se definen como derivaciones que actúan sobre funciones reales diferenciables, entonces la diferencial viene dada por

Aquí X ∈ T_xM, y por tanto X es una derivación definida sobre M y f es una función real sobre N. Por definición, la aplicación progrediente de X en un punto dado x de Mpertenece a T_φ(x)N y por tanto es una derivación.

Escogiendo cartas locales alrededor de x y φ(x), F viene determinada localmente por la aplicación diferenciable:

entre conjuntos abiertos de R^m y Rⁿ y dφ_x tiene representación (en x):

usado el convenio de sumación de Einstein, donde las derivadas parciales se evalúan en el punto de U que corresonde a x en la carta local dada. Extendiendo por linealidad esto da la siguiente matriz:

Por tanto la diferencial es una aplicación lineal, entre espacios tangentes, asociados a ala aplicación diferenciable φ en cada punto. Por tanto, en ciertas coordenadas locales, se representa por una matriz jacobiana de R^m en Rⁿ. En general, la diferencial no tiene porqué ser invertible (por ejemplo si m > n, pero no sólo en esos casos). Si φ es un difeomorfismo local, entonces la aplicación progrediente en x es invertible y su inversa da precisamente la aplicación regrediente en T_φ(x)N.

La aplicación diferencial frecuentemente se expresa unsando una gran variedad de notaciones distintas, entre las más comunes son:

Se sigue de la definición que la aplicación diferencial de una composición de aplicaciones es la composición de aplicaciones diferenciables. Ese hecho es el equivalente de la regla de la cadena para aplicaciones diferenciables entre variedades. Asimismo, la aplicación diferencial de un difeomorfismo local es un isomorfismo lineal de espacios vectoriales tangentes.

Extensión de la diferencial al fibrado tangente

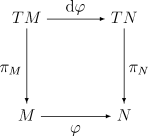
La aplicación diferencial de una aplicación diferenciable φ induce, de una manera obvia, una aplicación entre fibrados (de hecho un homeomorfismo de fibrados vectoriales) del fibrado tangente de M al fibrado tangente de N, denotado como dφ o φ_*, que hace que el siguiente diagrama conmute:

donde π_M y π_N denotan las proyecciones de los fibrados tangentes de M y N respectivamente.

Equivalentemente, φ_* = dφ es una aplicación entre fibrados de TM al fibrado regrediente φ^*TN sobre M, que podría a su vez ser visto como una sección del fibrado tangente Hom(TM,φ^*TN) sobre M.

Progredientte de campos vectoriales

Dada una aplicación diferenciable φ:M→N y un campo vectorial X sobre M, no siempre es posible definir una campo sobre N que sea la imagen por la aplicación progrediente de X asociada a φ. Por ejemplo, si la aplicación φ no es suprayectiva, no existe ninguna manera natrual de definir una "progresión" (extensión de imagen por la aplicación progrediente) fuera de la imagen por φ. De la misma manera, si φ no es inyectiva puede haber más de una elección para dicha "progresión" en un punto dado. Nevertheless, one can make this difficulty precise, using the notion of a vector field along a map.

Una sección del fibrado tangente de φ^*TN sobre M se llama is called a campo vectorial a través de φ. Por ejemplo, si M es una subvariedad de N y φ es su inclusión, entonces un campo vectorial a través de φ es precisamente una sección del fibrado tangente de N a lo largo de M; en particular, un campo vectorial sobre M define una sección de ese tipo vía la inclusión TM dentro de TN. Esta idea se generaliza a aplicaciones diferenciables cualesquiera.

Supóngase que X es un campo vectorial sobre M, i.e., una sección de TM. Entonces, aplicando la aplicación diferenical puntualmente a X se tiene la aplicación progrediente φ_*X, que es un campo vectorial a través de φ, i.e., una sección de φ^*TN sobre M.

aproximación lineal es una aproximación de una función cualquiera usando unatransformación lineal. Por ejemplo, dada una función diferenciable f de una variable real, se puede expresar (generalizada en el Teorema de Taylor) de la siguiente manera:

donde  es una función que representa el error usando la notación de Landau (Así,  tiende a 0 cuando tiende a ). La aproximación se obtiene al despreciar la suma de esta función error.

Lo cual es cierto para los valores de x cercanos a a. La expresión derecha es la de la recta tangente a la gráfica de fen a. Por esta razón también se llama aproximación de la recta tangente

Ejemplo

1.Para encontrar la aproximación lineal de  se hace lo siguiente:

1. Considérese la función 
2. Se tiene la derivada:

   

3. Según lo ya visto,

   

4. El resultado, 2.926, está razonablemente cerca del valor que puede dar una calculadora 2.924…

Aproximación lineal.

Tratamos en este apartado de justificar que para valores de “x” muy próximos a un número real “a” se tiene que:

Para ello veamos que es, desde el punto de vista geométrico, F(a) + F(a) (x-a)   para una función dada F(x) derivable en el punto x = a.

Recordemos que la ecuación de una recta en R² que pasa por un punto (x₀, y₀) y tiene de pendiente “m” tenía la forma:

y-y₀ = m(x-x₀).

Sea el punto (a , F(a))  y sea m = F’(a)  la pendiente de dicha función en el punto x = a. La ecuación de la recta será   y – F(a) = F’(a) (x - a)  es decir: 

y = F(a) + F ’(a) (x - a)

con lo cual tenemos que la expresión anterior representa la ecuación de la recta tangente a la gráfica de la función F(x) en el punto x = a:

Por ejemplo, si consideramos la función:

F(x) = x³ – x² – 8x  + 12

cuya gráfica en el intervalo [-4, 4] es:

y consideramos el punto x = 3, la ecuación de la tangente a la curva en dicho punto se obtendrá:

F(3) + F ’(3)(x – 3) = -33+13x

Su representación gráfica, junto con la función anterior es:

Claramente se observa como, en puntos cercanos a x =3, las gráficas de ambas funciones se confunden, es por ello por lo que podemos afirmar que:

siempre en puntos cercanos a x =3 (en otros puntos se observa como es falso).

Por lo tanto,  F(3) + F '(3) (x-3)  es la aproximación lineal de la función F(x) en un entorno del punto x=3.

Si llamamos x – a = h, nos queda:

a la expresión  F’(a) h  se le suele llamar diferencial de la función F en el punto “a” y se denota por:

Aproximación cuadrática.

Llamamos aproximación cuadrática de una función F(x) de clase 2 a:

La cual vamos a aplicar al mismo ejemplo del apartado anterior:

F(3) + F ’(3)(x – 3) + (1/2) F ’’(3) (x – 3)² = 39 – 35x + 8x²

Si realizamos la representación gráfica de esta función cuadrática y de la gráfica de la función obtenemos:

y en ella se observa que, en un entorno del punto x=3 ambas gráficas se confunden, siendo ésta una “mejor aproximación” de la función que en el caso de la aproximación lineal del apartado anterior.

Aproximación polinómica de orden superior de una función

En general, dada una función de clase k, podemos aproximarla:

expresión que se conoce como la fórmula de Taylor, y su significado ha quedado suficientemente claro en el desarrollo expuesto. Al último término del desarrollo le hemos llamado “Resto” y es una función de (x-a).

Cuantos más términos tenga la Fórmula de Taylor para una función dada, conseguiremos una mayor aproximación de la función en el punto dado, como vimos en el ejemplo anterior.

Ejemplo

Dada la función:

F(x) = Log(x)

Obtener una aproximación de ella  en el entorno del número e:

a) De orden uno.

b) De orden cuatro.

Solución:

Para calcular la fórmula de Taylor hemos de conocer las sucesivas derivadas hasta el orden pedido, evaluadas en el punto en cuestión, en nuestro caso, e.  Para el apartado a):

F(x) = Log(x) Þ F(e) = 1

F’(x) =  1/x  Þ   F’ (e) =  1/e

Por lo que el desarrollo de Taylor de orden uno resulta:

b) Para el desarrollo de Taylor de orden cuatro, hemos de calcular hasta la cuarta derivada:

Sustituyendo:

Ambas son aproximaciones de la función Log(x), pero la primera es mejor que la segunda. Gráficamente podemos observar este hecho; para lo cual representamos Log(x):

Y ahora representamos en la misma gráfica las aproximaciones de orden 1 (lineal) y la de orden 4:

Se observa como, en el entorno del número e ( = 2’71828...) ambas aproximaciones coinciden con la gráfica de la función, siendo la de orden 4 una mejor aproximación que la de orden 1, ya que en un entorno de e se aproxima mucho mejor.