Cálculo diferencial
criterio de la derivada de mayor orden es usado para encontrar máximos, mínimos, y puntos de inflexión en la curva de un polinomio de grado n.
El criterio
 ;
; existe y no es cero.
existe y no es cero.
Entonces,
- si n es par
 es un punto máximo local.
es un punto máximo local. es un punto mínimo local.
es un punto mínimo local.
- si n es impar
 es un punto de inflexión decreciente.
es un punto de inflexión decreciente. es un punto de inflexión creciente.
es un punto de inflexión creciente.
Recordando que los puntos de inflexión son crecientes y decrecientes dependiendo del cambio de la concavidad antes y después del punto de inflexión.
La derivada de la derivada de una función se conoce como segunda derivada de la función, es decir, si f(x) es una función y existe su primera derivada f´(x), en el caso de que se pueda obtener, la derivada de la función obtenida de aplicar la derivada se le llama segunda derivada:
de manera similar se puede obtener las derivadas de mayor orden, sin embargo es necesario aclarar que las derivadas de una función dependen de las características de la función y es posible, y frecuentemente sucede, que algunas derivadas existen pero no para todos los ordenes pese a que se puedan calcular con las formulas. Es necesario considerar los teoremas expuestos en la sección de los teoremas.
Las notaciones usuales utilizadas para derivadas de segundo orden son:
para derivadas de orden superior es de forma similar, así por ejemplo tendríamos las siguientes derivadas:
Ejemplos:
Dada la función  obtener la segunda derivada y cuarta derivada:
obtener la segunda derivada y cuarta derivada:
a) Solución:
derivando
b) Solución:
para la primera derivada obtenemos
como podemos ver, en este caso la función es derivable a cualquier orden. Al igual que en el caso anterior.
c).- Solución
para la primera derivada obtenemos:
d).- Solución:
obteniendo la primera derivada de la función (línea recta) obtenemos:
al sacar la derivada a está línea paralela al eje x, obtenemos
como podemos observar no tiene sentido sacar las derivadas de orden superior.
Criterio de la primera derivada al método o teorema utilizado frecuentemente en el cálculo matemático para determinar los mínimos y máximos relativosque pueden existir en una función mediante el uso de la primera derivada o derivada principal, donde se observa el cambio de signo, en un intervalo abierto señalado que contiene al punto crítico  .
.
 .
.Teorema valor máximo y mínimo
"Sea  un punto crítico de una función
un punto crítico de una función  que es continua en un intervalo abierto
que es continua en un intervalo abierto  que contiene a
que contiene a  . Si
. Si  es derivable en el intervalo, excepto posiblemente en
es derivable en el intervalo, excepto posiblemente en  , entonces
, entonces  puede clasificarse como sigue."
puede clasificarse como sigue."
 un punto crítico de una función
un punto crítico de una función  que es continua en un intervalo abierto
que es continua en un intervalo abierto  que contiene a
que contiene a  . Si
. Si  es derivable en el intervalo, excepto posiblemente en
es derivable en el intervalo, excepto posiblemente en  , entonces
, entonces  puede clasificarse como sigue."
puede clasificarse como sigue."
1. Si  '
' cambia de positiva a negativa en
cambia de positiva a negativa en  , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
.
 '
' cambia de positiva a negativa en
cambia de positiva a negativa en  , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
.
2. Si  '
' cambia de negativa a positiva en
cambia de negativa a positiva en  , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
 '
' cambia de negativa a positiva en
cambia de negativa a positiva en  , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
3. Si  '
' es positiva en ambos lados de
es positiva en ambos lados de  o negativa en ambos lados de c, entonces
o negativa en ambos lados de c, entonces  no es ni un mínimo ni un máximo relativo.
no es ni un mínimo ni un máximo relativo.
 '
' es positiva en ambos lados de
es positiva en ambos lados de  o negativa en ambos lados de c, entonces
o negativa en ambos lados de c, entonces  no es ni un mínimo ni un máximo relativo.
no es ni un mínimo ni un máximo relativo.
La base del presente criterio radica en observar que los máximos o mínimos locales son consecuencia de observar los siguientes hechos:
1.- Cuando la derivada es positiva la función crece.
2.- Cuando la derivada es negativa la función decrece.
3.- Cuando la derivada es cero la función tiene un máximo o un mínimo.
Sea f(x) una función y c un número en su dominio. Supongamos que existe a y b con a



1.- f es continua en el intervalo abierto (a,b) (de acuerdo con el teorema de Rolle)
2.- f es derivable en el intervalo abierto (a,b), excepto quizá en c;
3.- f´(x) es positiva para todo x en el intervalo y negativa para todo x>c en el intervalo.
Entonces f tiene un máximo local en c.
Nótese que un criterio similar puede tenerse para obtener un mínimo local, solo es necesario intercambiar “positivo” por “negativo”.
De manera intuitiva podemos observar que para determinar si existe un máximo o un mínimo basta graficar alrededor de los puntos donde se ha presentado un cambio de signo Es también importante tener en consideración que el termino alrededor del cambio de signo de la derivada de la función es muy relativo y es este punto donde tenemos que tener la máxima consideración.
Un punto mas a considerar es el tener en cuenta que solo es necesario considerar no solo el cambio de signos para la derivada Por ejemplo, para el caso de la función:
la función entre el intervalo (-1,1) tiene un cambio de signo, sin embargo, la función no es diferenciable en el punto x = 0, pese a eso si existe un mínimo local.
El Criterio de la segunda derivada es un teorema o método científico del cálculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simplemente correspondiente a los máximos y mínimos relativos de el criterio de la segunda derivada.
Se basa en el hecho de que si la gráfica de una función  (prima)es conexa en un intervalo abierto que contiene a
(prima)es conexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  . De manera similar, si la gráfica de una función es cóncava hacia abajo y hacia arriba en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo y hacia arriba en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
.
 (prima)es conexa en un intervalo abierto que contiene a
(prima)es conexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  . De manera similar, si la gráfica de una función es cóncava hacia abajo y hacia arriba en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo y hacia arriba en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
.Teorema
Sea  una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
 una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
- Si
 , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
. - Si
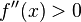 , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
- Si
 , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es,  quizás tenga un máximo relativo en
quizás tenga un máximo relativo en  , un mínimo relativo en
, un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
El Criterio o prueba de la Tercera Derivada es un método del cálculo matemático en el que se utiliza la tercera derivada de una función para confirmar o comprobar los puntos de inflexión obtenidos a partir de la segunda derivada. Es un caso particular del Criterio de la derivada de mayor orden.
Procedimiento
- Calcular las derivadas segunda y tercera de

- Hallar los puntos que cumplen

- Evaluar
 con los valores obtenidos en el paso anterior. Si es diferente de 0; entonces, es un punto de inflexión. En caso contrario, se debe usar el criterio de la derivada de mayor orden: si y solo si el menor orden de las derivadas superiores diferentes de cero es impar; el punto evaluado corresponde a uno de inflexión.
con los valores obtenidos en el paso anterior. Si es diferente de 0; entonces, es un punto de inflexión. En caso contrario, se debe usar el criterio de la derivada de mayor orden: si y solo si el menor orden de las derivadas superiores diferentes de cero es impar; el punto evaluado corresponde a uno de inflexión. - En la función original calculamos los valores de las ordenadas según se trate de una o de varias.
No hay comentarios:
Publicar un comentario