punto de inflexión es un punto donde los valores de x de una función continua pasa de un tipo de concavidad a otra. La curva "atraviesa" la tangente. Matemáticamente la derivada segunda de la función f en el punto de inflexión es cero, o no existe.
En el cálculo de varias variables a estos puntos de inflexión se les conoce como puntos de ensilladura.
Cálculo de los puntos de inflexión en funciones reales derivables de variable real
En las funciones derivables reales de una variable real, para hallar estos puntos de inflexión, basta con igualar la segunda derivada de la función a cero y despejar. Los puntos obtenidos deberán ser sustituidos en la derivada tercera o sucesivas hasta que nos dé un valor diferente de cero. Cuando esto suceda, si la derivada para la que es distinto de cero es impar, se trata de un punto de inflexión; pero, si se trata de derivada par, no lo es. Más concretamente:
- Se halla la primera derivada de
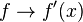
- Se halla la segunda derivada de

- Se halla la tercera derivada de
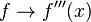
- Se iguala la segunda derivada a 0:
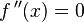
- Se despeja la variable independiente y se obtienen todos los valores posibles de la misma:
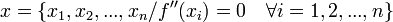 .
. - Se halla la imagen de cada
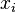 sustituyendo la variable dependiente en la función.
sustituyendo la variable dependiente en la función. - Ahora, en la tercera derivada, se sustituye cada
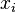 :
:- Si
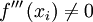 , se tiene un punto de inflexión en
, se tiene un punto de inflexión en 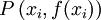 .
. - Si
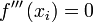 , debemos sustituir
, debemos sustituir 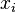 en las sucesivas derivadas hasta sea distinto de cero. Cuando se halle la derivada para la que
en las sucesivas derivadas hasta sea distinto de cero. Cuando se halle la derivada para la que 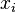 no sea nulo, hay que ver qué derivada es:
no sea nulo, hay que ver qué derivada es:- Si la derivada es impar, se trata de un punto de inflexión.
- Si la derivada es par, no se trata de un punto de inflexión.
- Si
La ecuación  no tiene puntos de inflexión, porque la derivada segunda es siempre mayor o igual a cero, por tanto no hay cambio de concavidad dado que es no negativa en todo su dominio. Sin embargo en
no tiene puntos de inflexión, porque la derivada segunda es siempre mayor o igual a cero, por tanto no hay cambio de concavidad dado que es no negativa en todo su dominio. Sin embargo en 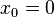 la derivada segunda se anula y la primera derivada no nula en
la derivada segunda se anula y la primera derivada no nula en 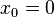 es la derivada cuarta, que es par. Obsérvese que
es la derivada cuarta, que es par. Obsérvese que  tampoco presenta un extremo en
tampoco presenta un extremo en  .
.
 no tiene puntos de inflexión, porque la derivada segunda es siempre mayor o igual a cero, por tanto no hay cambio de concavidad dado que es no negativa en todo su dominio. Sin embargo en
no tiene puntos de inflexión, porque la derivada segunda es siempre mayor o igual a cero, por tanto no hay cambio de concavidad dado que es no negativa en todo su dominio. Sin embargo en 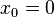 la derivada segunda se anula y la primera derivada no nula en
la derivada segunda se anula y la primera derivada no nula en 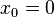 es la derivada cuarta, que es par. Obsérvese que
es la derivada cuarta, que es par. Obsérvese que  tampoco presenta un extremo en
tampoco presenta un extremo en  .
.PUNTOS DE INFLEXIÓN
DEFINICIÓN
El punto que, en una función continua, separa la parte convexa de la cóncava, se llama punto de inflexión de la función. En ellos la función no es cóncava ni convexa sino que hay cambio de concavidad a convexidad o al revés.
Los puntos de inflexión están caracterizados por:
TEOREMA
Los puntos de inflexión están caracterizados por:
TEOREMA
Sea
Si
|
Clasificación de los puntos de inflexión
Nota
Los puntos de inflexión donde la función es derivable, tienen la característica de tener una recta tangente que cruza la gráfica de f.
Ejemplo:


Ejemplo:
El punto x=1 es un punto de inflexión, puesto que antes de x=1 la derivada segunda es negativa (convexa) y después de x=1 es positiva (cóncava).
punto de silla o punto de ensilladura es el punto sobre una superficie en el que la pendiente es cero pero no se trata de un extremo local (máximo o mínimo). Es el punto sobre una superficie en el que la elevación es máxima en una dirección y mínima en la dirección perpendicular. El nombre proviene del parecido con una silla de montar de las superficies en torno a un punto de silla.
Definición
Matemáticamente se define como un punto de una función en el que la primera derivada es nula, mientras que el signo de la segunda derivada (curvatura) depende de la dirección en que se calcule. Si en un punto de una función de dos variables  el gradiente es cero, sólo puede tratarse de un máximo, un mínimo o un punto de silla.
el gradiente es cero, sólo puede tratarse de un máximo, un mínimo o un punto de silla.
 el gradiente es cero, sólo puede tratarse de un máximo, un mínimo o un punto de silla.
el gradiente es cero, sólo puede tratarse de un máximo, un mínimo o un punto de silla.Propiedades
En consonancia con su definición, el punto de ensilladura es el más elevado que permite conectar los dos dominios altos adyacentes y es también el paso más bajo que comunica los dos dominios adyacentes que quedan por debajo. Otra propiedad de estos puntos es que por ellos pasa la curva de nivel más profunda que conecta dos dominios elevados, que determina la elevación a la que hay que descender para caminar de una montaña a otra. Por un punto de ensilladura pasa también el camino más bajo que cruza entre dos máximos de la superficie (dos montañas).
Relevancia
Al describir el relieve terrestre se usan dos términos equivalentes: collado de montaña (equivalente continental del umbral) y umbral submarino. Un ejemplo es elUmbral de Camarinal, que separa el Océano Atlántico del Mar Mediterráneo. Por definición, los lagos tienen su desaguadero en un punto de silla de la topografía.
Ejemplo
Un ejemplo típico es el Paraboloide hiperbólico, la función en  :
:
 :
: .
.
Para determinar sus extremos relativos, calculamos su derivada parcial respecto a x:
en el punto donde esta derivada valga cero, puede ser un extremo relativo:
en el punto x = 0 puede haber un extremo relativo, calculando su derivada segunda vemos:
que es positiva, indicando un mínimo: siguiendo el eje de las x, en el punto x = 0 la función presenta un mínimo relativo.
Veamos esto mismo en la dirección del eje de las y, su derivada parcial primera es:
Cuando esta derivada primera valga cero, puede presentar un extremo relativo:
en el punto y = 0, se da esta circunstancia, si vemos su derivada segunda tenemos:
que toma valor negativo, luego este punto y = 0, es un máximo relativo, el punto x = 0, y = 0, es un punto de silla, dado que en la dirección del eje x es mínimo y en la dirección del eje y es un máximo.
Un punto estacionario de una función de una variable real,  , es un número
, es un número  donde la derivada de
donde la derivada de  es cero. Si la función
es cero. Si la función  es derivable y tiene un extremo local en un punto, ese punto estará entre sus puntos estacionarios.
es derivable y tiene un extremo local en un punto, ese punto estará entre sus puntos estacionarios.
 , es un número
, es un número  donde la derivada de
donde la derivada de  es cero. Si la función
es cero. Si la función  es derivable y tiene un extremo local en un punto, ese punto estará entre sus puntos estacionarios.
es derivable y tiene un extremo local en un punto, ese punto estará entre sus puntos estacionarios.
Igualmente, un punto estacionario de una función 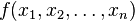 de varias variables reales, es un punto
de varias variables reales, es un punto  donde se anulan simultáneamente todas sus derivadas parciales. Si la función
donde se anulan simultáneamente todas sus derivadas parciales. Si la función  es diferenciable, los puntos donde tiene un extremo están entre los puntos estacionarios de la función.
es diferenciable, los puntos donde tiene un extremo están entre los puntos estacionarios de la función.
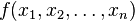 de varias variables reales, es un punto
de varias variables reales, es un punto  donde se anulan simultáneamente todas sus derivadas parciales. Si la función
donde se anulan simultáneamente todas sus derivadas parciales. Si la función  es diferenciable, los puntos donde tiene un extremo están entre los puntos estacionarios de la función.
es diferenciable, los puntos donde tiene un extremo están entre los puntos estacionarios de la función.
regla de l'Hôpital o regla de l'Hôpital-Bernoulli1 es una regla que usa derivadas para ayudar a evaluar límites de funciones que estén en forma indeterminada.2
Esta regla recibe su nombre en honor al matemático francés del siglo XVII Guillaume François Antoine, marqués de l'Hôpital (1661 - 1704), quien dio a conocer la regla en su obra Analyse des infiniment petits pour l'intelligence des lignes courbes (1696), el primer texto que se ha escrito sobre cálculo diferencial, aunque actualmente se sabe que la regla se debe a Johann Bernoulli, que fue quien la desarrolló y demostró.1 La explicación es que ambos habían entrado en un curioso arreglo de negocios por medio del cual el marqués de L'Hospital compró los derechos de los descubrimientos matemáticos de Bernoulli.
Enunciado
La regla de L'Hôpital es una consecuencia del Teorema del valor medio de Cauchy que se da sólo en el caso de las indeterminaciones del tipo  o
o 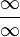 .4 5 6
.4 5 6
 o
o 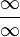 .4 5 6
.4 5 6
|
Demostración
El siguiente argumento se puede tomar como una «demostración» de la regla de L'Hôpital, aunque en realidad, una demostración rigurosa de la misma requiere de argumentos de tipo ε-δ más delicados.4 6
- Como g(c)=0 y g'(x)≠0 si x≠c, se tiene que g(x)≠0 si x≠c como consecuencia del Teorema de Rolle.
- Dado que f(c)=g(c)=0, aplicando el Teorema del Valor Medio de Cauchy, para todo x en (a,b), con x distinto de c, existe tx en el intervalo de extremos a y b, tal que el cociente f(x)/g(x) se puede escribir de la siguiente manera:
- Cuando x tiende hacia c, por la regla del sándwich, tx también tiende hacia c, así que:
Nota: el último paso al límite, aunque es cierto, requeriría una justificación más rigurosa.
Ejemplos
La regla de l'Hôpital se aplica para salvar indeterminaciones que resultan de reemplazar el valor numérico al llevar al límite las funciones dadas. La regla dice que, se deriva el numerador y el denominador, por separado; es decir: sean las funciones originales f(x)/g(x), al aplicar la regla se obtendrá: f'(x)/g'(x).
Aplicación sencilla
Aplicación consecutiva
Mientras la función sea n veces continua y derivable, la regla puede aplicarse n veces:
Adaptaciones algebraicas
Dada la utilidad de la regla, resulta práctico transformar otros tipos de indeterminaciones al tipo  mediante transformaciones algebraicas:
mediante transformaciones algebraicas:
 mediante transformaciones algebraicas:
mediante transformaciones algebraicas:Cocientes incompatibles
Las indeterminaciones de tipo  se pueden transformar mediante la doble inversión de los cocientes:
se pueden transformar mediante la doble inversión de los cocientes:
 se pueden transformar mediante la doble inversión de los cocientes:
se pueden transformar mediante la doble inversión de los cocientes:
De esta forma se puede demostrar que las indeterminaciones de tipo  también se pueden resolver por medio de la aplicación de la regla de L'Hôpital de forma directa, sin aplicación de la doble inversión.
también se pueden resolver por medio de la aplicación de la regla de L'Hôpital de forma directa, sin aplicación de la doble inversión.
 también se pueden resolver por medio de la aplicación de la regla de L'Hôpital de forma directa, sin aplicación de la doble inversión.
también se pueden resolver por medio de la aplicación de la regla de L'Hôpital de forma directa, sin aplicación de la doble inversión.Indeterminaciones no cocientes
A veces algunos límites indeterminados que no se presentan como cocientes pueden ser resueltos con esta regla, recurriendo a transformaciones previas que lleven a un cociente del tipo  ó
ó  .
.
 ó
ó  .
.- Tipo

- Se trata de hacer una transformación como
 ó
ó 
El más clásico:
- Tipo
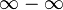
Generalizaciones
- La regla de L'Hôpital vale para límites laterales, límites en el infinito y límites infinitos.
- La regla de L'Hôpital se puede extender a funciones escalares de n variables que sean diferenciables. Dadas dos funciones diferenciables f y g tales que f(c) = g(c) = 0, se tiene:
 , representan los gradientes de ambas funciones escalares.
, representan los gradientes de ambas funciones escalares.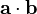 , representa el producto escalar de dos vectores.
, representa el producto escalar de dos vectores. , representa la norma de un vector.
, representa la norma de un vector. , es el ángulo formado por el gradiente de f y el vector
, es el ángulo formado por el gradiente de f y el vector  .
. , es el ángulo formado por el gradiente de g y el vector
, es el ángulo formado por el gradiente de g y el vector  .
.
























No hay comentarios:
Publicar un comentario