Cálculo diferencial
ángulo hiperbólico es una figura geométrica que divide a la
hipérbola. Las relaciones del ángulo hiperbólico se asemejan a la relación que existe entre un
ánguloordinario y un
círculo. El ángulo hiperbólico es definido para una "posición estándar", y se lo asocia con la
medida de un intervalo de una rama de una hipérbola.
Un ángulo hiperbólico en posición estándar es el ángulo en (0, 0) entre el rayo hasta (1, 1) y el rayo hasta (x, 1/x) donde x > 1.
Notar que a diferencia del ángulo circular, el ángulo hiperbólico no se encuentra
acotado, tal como sucede con la función
ln x, una característica relacionada con la naturaleza no acotada de las
series armónicas. El ángulo hiperbólico en posición estándar es considerado negativo cuando 0 <
x < 1.
Supóngase que
ab = 1 y
cd = 1 con
c >
a > 1 de forma tal que (
a,
b) y (
c,
d) determinan un intervalo sobre la hipérbola
xy = 1. Entonces el mapeo de compresión con elementos diagonales
b y
a mapea este intervalo al ángulo hiperbólico en posición estándar que va desde (1, 1) a (
bc,
ad). De acuerdo a la relación descubierta por
Gregoire de Saint-Vincent, el sector hiperbólico determinado por (
a,
b) y (
c,
d) tiene la misma área que este ángulo en posición estándar, y la magnitud del ángulo hiperbólico corresponde con esta área.
El ángulo_hiperbólico
u es un número real que es el argumento de las
funciones hiperbólicas sinh y cosh. Determina un sector hiperbólico (rojo) que tiene un área
u. Las ramas del
triángulo hiperbólico(amarillo) son proporcionales a sinh(
u) y cosh(
u).

Superior: Ángulos hiperbólicos positivo y negativo.
Inferior: La diferencia entre dos ángulos positivos se muestra como Δ
u =
u2−
u1.
integración simbólica es el problema de encontrar una fórmula para la
antiderivada, o
integral indefinida, de una función,
f(
x), i.e. encontrar la
función diferenciable F(
x) de tal manera que:

Esto también se escribe como:
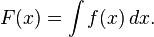
Discusión
El término
simbólico se usa para distinguir este problema de la
integración numérica, en donde el valor de
F de una cierta abscisa o cierto conjunto de abscisas, en lugar de una fórmula general para
F, se busca.
Ambos problemas tenían importancia práctica y teorética antes de la edad de las computadoras digitales, pero ahora son más del campo de las
ciencias de la computación, porque las computadoras se usan lo más frecuentemente para evaluar los instantes individuales hoy día.
Evaluar la derivada de una expresión es un processo directo para cual es fácil crear un
algoritmo. La pregunta opuesta de evaluar la integral es mucho más difícil. Muchas expresiones que son relativamente sencillas no tienen integrales que se pueden expresar en una
forma cerrada.
Sin embargo, el
algoritmo de Risch sólo se aplica a las
integrales indefinidas y la mayoría de las integrales de interés a los físicos, químicos teoréticos e ingenieros son 'integrales definidas que a menudo están relacionadas con las
Transformadas de Laplace, las
Transformadas de Fourier y las
Transformadas de Mellin. Carente de un algoritmo general, los desarrolladores de los
sistemas algebraicos computacionales, han implementado
heurísticas basadas en el casamento de patrones y la explotación de funciones especiales, particularmente la
función gamma incompleta1 Aunque esta estrategia es heurística en vez de algorítmico, Sin embargo, es un método eficaz de resolver muchas integrales definidas encontradas por aplicaciones prácticas de la ingeniería. Los sistemas anteriores tal como Macsyma tenían algunas integrales definidas relacionadas con funciones elementales dentro de una tabla de consulta. Aunque este método particular, que conllevan las derivadas de funciones especiales con respecto a sus parámetros, transformaciones de variables, casamentos de patrones, y otras manipulaciones, fue liderado por los desarrolladores del sistema
Maple2 y luego fueron emulados por
Mathematica,
Axiom,
MuPAD y otros sistemas.
Ejemplo
Por ejemplo:

![\int_{-1}^1 x^2\,dx = \left[\frac{x^3}{3}\right]_{-1}^1= \frac{1^3}{3} - \frac{(-1)^3}{3}=\frac{2}{3}](https://upload.wikimedia.org/math/2/0/f/20f8d3acd558b289ca0e9ea591933c9c.png)
es un resultado símbolico para una integral definida, y

es un resultado numérico para la misma integral definida.
Linealización de modelos
|
Existen diversos modelos que, no siendo directamente modelos lineales, admiten una transformación que los permite estudiar a partir de la teoría vista como modelos lineales.
Son los siguientes:
Modelo exponencial
Si se sospecha de una relación exponencial entre las variable X e Y:
se verifica:
Con lo cual podemos ajustar el modelo transformando logarítmicamente la variable Y, y resolviendo el modelo lineal.
Si sospechamos de una relación del tipo:
se verifica que:
y podemos resolver el modelo transformando logarítmicamente las variables X e Y, y solucionando el modelo lineal resultante.
Se trata de resolver el modelo :
resolviendo el modelo lineal con la transformada logarítmica de X.
|
- notación de Leibniz —llamada así en honor del filósofo y matemático alemán del siglo XVII Gottfried Wilhelm Leibniz—, utiliza los símbolos dx y dy para representar incrementos infinitamente pequeños (o infinitesimales) de x e y, respectivamente, al igual que Δx y Δy representan incrementos finitos de x e y, respectivamente.
Historia
El método de Newton-Leibniz de
cálculo infinitesimal se introdujo en la segunda mitad del siglo XVII. Mientras que Newton no tenía una notación estándar para la integración, Leibniz comenzó a usar el carácter
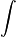
. Se basó en el carácter de la palabra latina
summa ('suma'), que escribió
ſumma con la
alargada entonces comúnmente utilizado en Alemania en el momento. Este uso apareció por primera vez públicamente en su artículo
De Geometria, publicado en
Acta Eruditorum de junio de 1686,
2 pero que había estado utilizando en manuscritos privados por lo menos desde 1675.
3
Definición de la notación
La notación de Leibniz tradicional

es utilizada para indicar que la variable independiente es
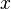
y la variable dependiente es
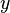
, por lo tanto existen otras notaciones comunes para la derivada:
4
- donde las notaciones
 y
y  son operadores de derivación porque indican la operación de derivación.
son operadores de derivación porque indican la operación de derivación.
- La notación
 introducida por Leibniz es solo un sinónimo de
introducida por Leibniz es solo un sinónimo de  . Sin embargo, es una notación útil cuando se usa en la notación de incrementos. Con base en la ecuación razón (instantánea) de cambio de
. Sin embargo, es una notación útil cuando se usa en la notación de incrementos. Con base en la ecuación razón (instantánea) de cambio de 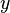 con respecto a
con respecto a 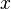 dónde
dónde  ,
,  , al escribir de nuevo la definición de derivada en la notación de Leibniz en la forma:
, al escribir de nuevo la definición de derivada en la notación de Leibniz en la forma:
Por lo tanto, en esta notación se representa la operación de diferenciar. Dada una
función f de
x:
mediante el operador
derivada de la función: {{ecuación|

se representaría de este modo
como un cociente de diferenciales. La belleza y utilidad de esta notación consiste en que permite recordar intuitivamente varios conceptos básicos del
cálculo tales como la
regla de la cadena. Dadas las funciones:
que con esta notación parece obvia debido a la cancelación de diferenciales (a pesar de que este razonamiento es incorrecto
[cita requerida])
Aparición en Principia
En la primera edición americana del libro se hace una introducción a la vida de Newton. En esta introducción, redactada por N. W. Chittenden, se comenta en una de las páginas que
el método diferencial es único y el mismo que el método de las fluxiones, excepto en el nombre y en la notación; el señor Leibniz llama a estas cantidades diferencias, a las cuales el señor Newton llama momentos, o fluxiones; y [Leibniz] las nota con una letra
d, una notación no usada por el señor Newton.
5
Aplicaciones
La notación de
Leibniz también es especialmente útil cuando se trabaja con
derivadas parciales de funciones multivariables y sus operadores derivados (
gradiente,
laplaciano,
rotacional,
divergencia, etc.) ya que indica en cada momento la variable de la función que se considera independiente, dejando el resto de variables como constantes en lo que se refiere a la derivación parcial.
- Notación de Leibnz para Derivadas:
En esta notación se representa la operación de diferenciar mediante el operador

, es decir, la operación "
derivada de la función f respecto de x" se representaría de este modo

como un cociente de diferenciales. La belleza y utilidad de esta notación consiste en que permite recordar intuitivamente varios conceptos básicos del cálculo tales como la regla de la cadena, que con esta notación parece obvia debido a la cancelación de diferenciales (a pesar de que este razonamiento es incorrecto)

; o bien el concepto de separación de variables en la resolución de ecuaciones diferenciales

.
La notación de Leibniz también es especialmente útil cuando se trabaja con derivadas parciales de funciones multivariables y sus operadores derivados (gradiente, laplaciano, rotacional, divergencia, etc.) ya que indica en cada momento la variable de la función que se considera independiente, dejando el resto de variables como constantes en lo que se refiere a la derivación parcial.
- Notación para derivadas de orden superior.
Se utiliza la siguientes notaciones para representar las derivadas de orden superior
1ra Derivada
2da Derivada
3ra Derivada
n-Derivada
Cuando el orden de la derivada es mayor a o igual a 4 hay ciertas notaciones que ya no se utilizan.



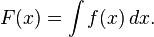

![\int_{-1}^1 x^2\,dx = \left[\frac{x^3}{3}\right]_{-1}^1= \frac{1^3}{3} - \frac{(-1)^3}{3}=\frac{2}{3}](https://upload.wikimedia.org/math/2/0/f/20f8d3acd558b289ca0e9ea591933c9c.png)

 . Se basó en el carácter de la palabra latinasumma ('suma'), que escribió ſumma con la
. Se basó en el carácter de la palabra latinasumma ('suma'), que escribió ſumma con la  es utilizada para indicar que la variable independiente es
es utilizada para indicar que la variable independiente es 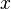 y la variable dependiente es
y la variable dependiente es 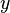 , por lo tanto existen otras notaciones comunes para la derivada:
, por lo tanto existen otras notaciones comunes para la derivada:
 y
y  son
son  . Sin embargo, es una notación útil cuando se usa en la notación de incrementos. Con base en la ecuación razón (instantánea) de cambio de
. Sin embargo, es una notación útil cuando se usa en la notación de incrementos. Con base en la ecuación razón (instantánea) de cambio de  ,
,  , al escribir de nuevo la definición de derivada en la notación de Leibniz en la forma:
, al escribir de nuevo la definición de derivada en la notación de Leibniz en la forma:






No hay comentarios:
Publicar un comentario