INSTRUMENTOS EPÓNIMOS

Anillos de Raschig fabricados con material cerámico (diámetro: 25 mm).

Los anillos de Raschig (llamados así en honor a su inventor, el químico alemánFriedrich August Raschig) son piezas de geometría tubular cuyo diámetro es aproximadamente igual a su longitud y que se emplean como relleno para columnas en procesos de destilación y en otros procesos químicos ingenieriles. Generalmente se fabrican con material cerámico o metálico y poseen una elevada superficie específica, lo que facilita la interacción entre una fase líquida estacionaria y una fase móvil gaseosa.¹​

Los anillos de Raschig conforman lo que se conoce como relleno aleatorio, y el propio Friedrich Raschig logró llevar a cabo con ellos destilaciones mucho más eficientes que las que se conseguían empleando columnas de platos para destilación fraccionada.¹​

En la columna de destilación, el reflujo o vapor condensado gotea sobre el interior de la columna recubriendo los anillos de Raschig. Por otro lado, el vapor producido por la calefacción del dispositivo asciende por la columna. De esta forma, el vapor generado y el líquido condensado interaccionan en contracorriente en el interior de los anillos de Raschig, tendiendo a establecer un equilibrio. Los componentes menos volátiles se desplazan con el líquido condensado y los más volátiles se desplazan con el vapor generado (es decir, siguen sentidos opuestos).

Los anillos de Raschig se pueden emplear en dispositivos donde se requiera la interacción entre un gas y un líquido, ya sea con el fin de conseguir una absorción del gas, la separación de componentes presentes en la fase líquida o una reacción química. También se emplean en biorreactores como soporte de biopelículas.

Los anillos de Raschig fabricados con vidrio de borosilicato se emplean como relleno de depósitos y tanques que contienen disoluciones de material nuclear fisible (por ejemplo, disoluciones de nitrato de uranilo enriquecido). Su misión en estos casos es actuar como absorbentes de neutrones, disminuyendo el riesgo de accidentes potencialmente críticos.

Aparato de Kipp.

El aparato de Kipp, también denominado generador de Kipp, es un instrumento usado para la preparación de pequeños volúmenes de gases. Su nombre viene de su inventor, Petrus Jacobus Kipp.

Usos[editar]

Sus usos más comunes son la preparación de ácido sulfhídricomediante la reacción de ácido sulfúrico con sulfuro ferroso, preparación de dióxido de carbono mediante la reacción de ácido clorhídrico con carbonato de calcio, y de hidrógeno mediante la reacción de ácido clorhídrico con un metal apropiado.

Material[editar]

El aparato consiste en tres cilindros apilados. El material sólido (por ejemplo, sulfuro ferroso) se coloca en el cilindro del medio y el ácido en el superior. Un tubo se extiende del cilindro superior al inferior. El cilindro central tiene un tubo con una válvula utilizada para la extracción del gas obtenido. Cuando ésta está cerrada, la presión del gas en el cilindro central aumenta, empujando el ácido de vuelta al cilindro superior hasta que deja de estar en contacto con el material sólido, y la reacción cesa.

Los aparatos de Kipp suelen estar hechos de vidrio o polietileno.

Aparato de Kipp

Aparato de Kipp

El Aparato de Kipp, también llamado generador Kipp, es un aparato diseñado para la preparación de pequeños volúmenes de gases. Fue inventado en 1844 por el farmacéutico holandés Petrus Jacobus Kipp y ampliamente utilizado en laboratorios químicos.

Diseño y Funcionamiento del Aparato de Kipp

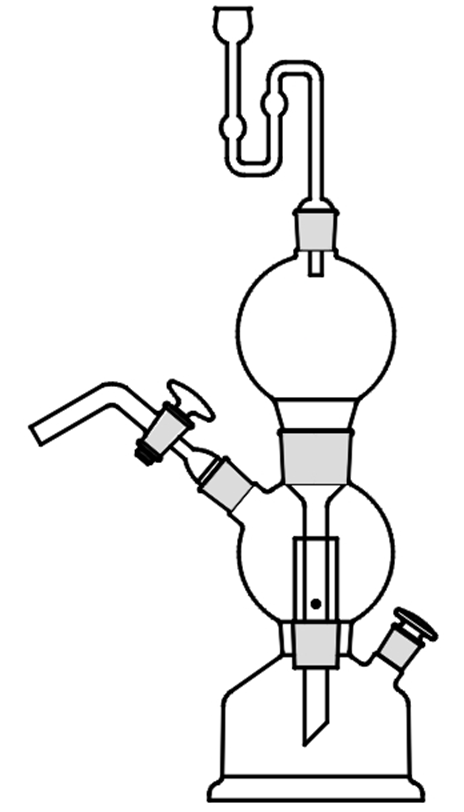
El aparato se hace generalmente de vidrio, o a veces de polietileno, y consta de tres cámaras apiladas verticalmente, parecidas a un muñeco de nieve. La cámara superior se extiende hacia abajo como un tubo que pasa a través de la cámara central hacia la cámara inferior. No existe un camino directo entre las cámaras media y superior, pero la cámara media está separada de la cámara inferior por una placa de retención, tal como una pieza cónica de vidrio con pequeños orificios, que permite el paso de líquido y gas.

Para producir gas, el material sólido se coloca en la cámara intermedia en grumos suficientemente grandes para evitar caer a través de la placa de retención. El líquido, tal como un ácido, se vierte en la cámara superior. Aunque el ácido es libre de fluir a través del tubo hacia la cámara inferior, se impide que suba allí por la presión del gas contenido por encima de él, Que es capaz de dejar el aparato sólo por una llave de paso cerca de la parte superior de la cámara intermedia. Esta llave de paso puede ser abierta, inicialmente para permitir que el aire salga del aparato, permitiendo que el líquido en la cámara inferior se eleve a través de la placa de retención en la cámara intermedia y reaccione con el material sólido. El gas se desprende de esta reacción, que se puede extraer a través de la llave de paso como se desee. Cuando se cierra la llave de paso, la presión del gas en la cámara intermedia se eleva y empuja el ácido hacia abajo hasta la cámara inferior, hasta que ya no está en contacto con el material sólido. En ese punto, la reacción química se detiene, hasta que la llave de paso se abre de nuevo y se extrae más gas.

Los generadores de Kipp sólo funcionan correctamente de la manera descrita si el material sólido es insoluble en el ácido, ya que de otro modo el material disuelto continuaría desarrollando gas incluso después de que el nivel disminuyera. El gas producido requiere a menudo purificación y/o secado adicional, debido al contenido de vapor de agua y posiblemente niebla si la reacción es vigorosa.

Ejemplos Gases Obtenidos con el Aparato de Kipp

Para un uso exitoso en un Aparato de Kipp, el material sólido tiene que estar disponible en grumos lo suficientemente grande como para permanecer en la placa de retención sin caer a través de sus agujeros.

• Dióxido de carbono utilizando carbonato de calcio y ácido clorhídrico.
• Acetileno a partir de carburo de calcio y agua.
• Ozono a partir de peróxido de bario y ácido sulfúrico concentrado.

máquina de Atwood es una máquina inventada en 1784 por George Atwood como un experimento de laboratorio para verificar las leyes mecánicas del movimiento uniformemente acelerado. La máquina de Atwood es una demostración común en las aulas usada para ilustrar los principios de la Física, específicamente en Mecánica.

La máquina de Atwood consiste en dos masas, ${\displaystyle m_{1}\;}$ y ${\displaystyle m_{2}\;}$, conectadas por una cuerda inelástica de masa despreciable con una polea ideal de masa despreciable.

• Cuando ${\displaystyle m_{1}\;=\ m_{2}}$, la máquina está en equilibrio neutral sin importar la posición de los pesos.
• Cuando ${\displaystyle m_{2}\;>\ m_{1}}$ ambas masas experimentan una aceleración uniforme.

Ecuación para la aceleración uniforme[editar]

Diagrama de cuerpo libre.

Se puede obtener una ecuación para la aceleración usando análisis de fuerzas. Puesto que se está usando una cuerda inelástica con masa despreciable y una polea ideal con masa despreciable, las únicas fuerzas que se tiene que considerar son: la fuerza tensión (${\displaystyle T}$) y el peso de las dos masas (${\displaystyle mg}$). Para encontrar el ${\displaystyle \sum F}$ tenemos que considerar las fuerzas que afectan a cada masa por separado (con el siguiente convenio de signos, suponiendo que ${\displaystyle m_{1}>m_{2}}$, la aceleración ${\displaystyle a}$ es positiva hacia "abajo" -con el mismo sentido de la aceleración de la gravedad ${\displaystyle g}$- en ${\displaystyle m_{1}}$ y hacia "arriba" -con el sentido contrario a la aceleración de la gravedad ${\displaystyle g}$- en ${\displaystyle m_{2}}$):

• fuerzas que afectan a ${\displaystyle m_{1}\;}$ : ${\displaystyle m_{1}g-T\;=\;m_{1}a}$ (donde ${\displaystyle g}$ y ${\displaystyle a}$ tienen el mismo sentido)
• fuerzas que afectan a ${\displaystyle m_{2}\;}$ : ${\displaystyle T-m_{2}g\;=\;m_{2}a}$ (donde ${\displaystyle T}$ y ${\displaystyle a}$ tienen el mismo sentido)

${\displaystyle \sum F=(m_{1}g+T)+(T+m_{2}g)=g(m_{1}+m_{2})=(m_{1}+m_{2})a}$

Usando la segunda Ley de Newton del movimiento se puede obtener una ecuación para la aceleración del sistema de Atwood .

${\displaystyle \sum F=ma}$

${\displaystyle a={\sum F \over m}}$

${\displaystyle \sum F=g(m_{1}+m_{2})}$

${\displaystyle m=(m_{1}+m_{2})\;}$

${\displaystyle a=g{m_{1}-m_{2} \over m_{1}+m_{2}}}$

El factor ${\displaystyle {m_{1}-m_{2} \over m_{1}+m_{2}}}$, con ${\displaystyle m_{1}>m_{2}}$, es el número adimensional denominado número de Atwood en honor de George Atwood.

[Nota: Inversamente, la aceleración debida a la gravedad (${\displaystyle g}$) puede obtenerse cronometrando el movimiento de los pesos y calculando un valor para la aceleración uniforme (${\displaystyle a}$): En el diagrama de la figura, si se parte de las masas alineadas y se mide el tiempo ${\displaystyle t_{12}}$ en el que se separan las masas una distancia vertical ${\displaystyle d_{12}}$, se cumple que ${\displaystyle d_{12}={1 \over 2}at_{12}^{2}}$. Entonces: ${\displaystyle g=({m_{1}+m_{2} \over m_{1}-m_{2}}){2d_{12} \over t_{12}^{2}}}$]

Ecuación para la tensión[editar]

Puede ser útil obtener una ecuación para la tensión en la cuerda. Para evaluar la tensión sustituimos la ecuación por la aceleración en cualquiera de las dos ecuaciones de fuerza.

${\displaystyle a=g{m_{2}-m_{1} \over m_{1}+m_{2}}}$

Por ejemplo sustituyendo en ${\displaystyle m_{2}a=T-m_{2}g\;}$, se obtiene:

${\displaystyle T=g{2m_{1}m_{2} \over m_{1}+m_{2}}}$

La tensión puede obtenerse de una forma similar de ${\displaystyle m_{1}a=m_{1}g-T\;}$

Ecuación para una polea no ideal[editar]

Para diferencias muy pequeñas de masa y entre ${\displaystyle m_{1}}$ y ${\displaystyle m_{2}}$, el momento de inercia (${\displaystyle I}$) sobre la polea de masa no despreciable de radio ${\displaystyle r}$ no puede ser despreciada. La aceleración angular de la polea viene dada por:

${\displaystyle \alpha ={a \over r}}$

En este caso, el torque total del sistema se convierte en:

${\displaystyle \tau _{Total}=\left(T_{2}-T_{1}\right)r=I\alpha -\tau _{friccion}}$

Implementaciones prácticas[editar]

Las ilustraciones originales de Atwood muestran el eje de la polea principal descansando sobre el borde de otras cuatro ruedas, para minimizar las fuerzas de fricción de los cojinetes. Muchas implementaciones históricas de la máquina siguen este diseño.

Un ascensor con un contrapeso se aproxima a una máquina de Atwood ideal y de ese modo alivia al motor conductor de la carga total de la cabina del ascensor —solo tiene que vencer la diferencia entre el peso y la inercia de las dos masas, contrapeso y cabina-. El mismo principio se usa para ferrocarriles funiculares con dos vagones conectados en vías inclinadas.

Una máquina de Atwood gigantesca

(c) Ángel Franco. Universidad del País Vasco. España. www.sc.ehu.es/sbweb/fisica/celeste/atwood/atwood.htm

La máquina de Atwood es un clásico ejemplo de la aplicación de la segunda ley de Newton. Consta de una polea fija y una cuerda inextensible y de masa despreciable que pasa por la polea y de cuyos extremos cuelgan dos masas.Primero, se considera que la polea tiene un momento de inercia despreciable y cuando se estudia la dinámica de rotación, se proporciona el dato del momento de inercia de la polea. En esta página, se estudia el movimiento de una máquina de Atwood gigantesca. Consta de una rueda que supondremos de masa despreciable, situada a altura grande sobre el suelo. Por la rueda pasa una cuerda inextensible y de masa despreciable del cual cuelgan dos masas iguales. Estudiaremos el efecto de la variación de la aceleración de la gravedad con la altura sobre el movimiento de los cuerpos. 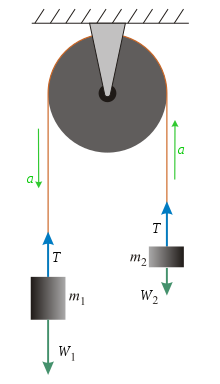La máquina de Atwood En la figura, se muestran las fuerzas sobre cada uno de los dos cuerpos, supondremos que m1>m2. Consideramos que la aceleración de la gravedad g es constante en módulo y dirección Aplicamos la segunda ley de Newton a cada uno de los cuerpos m1g-T=m1a T-m2g=m2a Despejamos la aceleración La velocidad de los cuerpos cuando el primero desciende una altura h partiendo del reposo es Aplicando el principio de conservación de la energía, se llega al mismo resultado. Comparamos el estado inicial y el estado final cuando el cuerpo de masa m1 desciende una altura h, y el cuerpo de masa m2asciende la misma altura. Ponemos el nivel cero de energía potencial en la posición inicial de los dos cuerpos. Igualamos la energía inicial y la energía final. Una máquina de Atwood gigantesca Si los dos cuerpos tienen la misma masa y están a la misma altura, la máquina de Atwood estará en equilibrio inestable. En cambio, si los dos cuerpos están inicialmente a distinta altura la variación de la aceleración de la gravedad con la altura hace que el cuerpo más cercano a la Tierra experimente una fuerza mayor que el cuerpo más alejado. Establecemos el origen en la posición de equilibrio de los dos cuerpos, cuando están a la misma altura H sobre la superficie de la Tierra. Se desplazan una distancia x los dos cuerpos, uno hacia arriba y otro hacia abajo. La fuerza que experimenta el cuerpo más cercano al suelo es y el más alejado Siendo R=6.37·106 m el radio de la Tierra, M=5.98·1024 kg la masa de la Tierra, G=6.67·10-11 Nm2/kg2, y m es la masa de cada uno de los dos cuerpos. Aplicamos la segunda ley de Newton a cada uno de los dos cuerpos F1-T=ma T-F2=ma Despejamos la aceleración a=(F1-F2)/(2m) Teniendo en cuenta que H y x son muy pequeños frente al radio R de la Tierra, podemos obtener una expresión sencilla de la aceleración a en función del desplazamiento x. Escribimos la ecuación del movimiento en forma de ecuación diferencial La solución de esta ecuación diferencial tiene la forma La velocidad de los cuerpos es Los coeficientes A y B se determinan a partir de las condiciones iniciales, en el instante t=0, el desplazamiento inicial es x=x0, y la velocidad inicial v=0. Las expresiones de la posición y velocidad de los cuerpos son Tiempo que tarda uno de los cuerpos en llegar al suelo. El cuerpo más cercano a la Tierra parte de la posición x=x0 en el instante t=0, y llega a la posición x=H en el instante t. Despejamos el tiempo t en la ecuación H=x0·cosh(kt) Haciendo el cambio de variable z=ekt, tenemos una ecuación de segundo grado en z. La raíz que da un tiempo t positivo es Como podemos apreciar el tiempo t depende del cociente H/x0. Se obtiene el mismo tiempo cuando H=100 y x0=10, que cuando H=10 y x0=1. Siempre que se cumpla que H<<R Balance energético Comparamos la situación inicial con la situación en el instante t (véase la segunda figura). Aplicamos el principio de conservación de la energía Dado el desplazamiento x calculamos la velocidad v de los cuerpos Ejemplo La posición de equilibrio de los dos cuerpos a la misma altura H=100 m. Se desplaza los dos cuerpos x0=10 m. Calcular el tiempo que emplea en llegar al suelo y la velocidad final de los bloques. Datos: Radio de la Tierra, R=6.37·106 m, Masa de la Tierra M=5.98·1024 kg, Constante G=6.67·10-11 Nm2/kg2, Aceleración de la gravedad en la superficie de la Tierra g=GM/R2=9.83 m/s2 Aplicando el principio de conservación de la energía v=0.247 m/s https://www.upct.es