INSTRUMENTOS EPÓNIMOS

Un prisma de Schmidt-Pechan, visto de lado y en perspectiva isométrica.

Un prisma de Schmidt-Pechan es un tipo de prisma óptico usado para rotar 180º una imagen sin invertirla. Se suelen montar en prismáticos para enderezar la imagen que entrega la lente.

Consiste en un par de prismas separados por un espacio vacío. Las reflexiones totales internas en su interior causan el giro de la imagen. Debido al prisma de techo del segundo prisma la imagen se rota pero no se invierte. Para que la reflexión sea eficiente algunas de las superficies reflectantes deben estar metalizadas ya que el ángulo de incidencia es menor que el ángulo crítico de la reflexión total interna.

Esta configuración es más compacta que otros diseños similares como el prisma de Porro o el prisma de Abbe-Koenig, aunque el mayor número de reflexiones y el espacio de aire entre los prismas hacen que la luz pierda más intensidad en su trayectoria a través de él. Asimismo las numerosas reflexiones causan un cierto cambio de fase debido a la polarización, de modo similar a lo que sucede en el rombo de Fresnel, lo que obliga a emplear recubrimientos de correción de fase sobre las superficies ópticas para evitar interferencias en la imagen.

Un prisma de techo de Amici es un tipo de prisma reflector usado para desviar 90º un haz de luz o una imagen, que además, se invierte. Se usa normalmente en los oculares de los telescopios como corrector de imagen.

Prisma del tipo usado en los oculares de los telescopios.

Su nombre se debe a su inventor, el astrónomo y óptico italiano Giovanni Amici. El prisma funciona igual que un prisma de ángulo recto con la particularidad de que la faceta reflectiva está tallada en forma de "prisma de techo",¹​ con dos facetas en ángulo de 90º. La reflexión interna total sobre estas facetas invierte la imagen sobre el eje vertical. Para mejorar la reflexión, a las facetas reflectoras se les da en ocasiones un recubrimiento metálico lo que permite que el prisma sea usado en un ángulo más amplio que el que permiten las leyes de la reflexión total interna.

Este prisma no debe confundirse con el prisma dispersivo de Amici.

Un Prisma de Wollaston es un tipo de prisma óptico que separa la luz entrante en dos haces polarizados ortogonalmente.

Fue inventado por el químico inglés William Hyde Wollaston el cual, unió con pegamento óptico por la hipotenusa dos prismas triangulares rectos formados de calcita (espato de Islandia) con ejes ópticos perpendiculares. La luz entra por una de las facetas laterales y se divide en dos haces al incidir en el corte diagonal. Los haces salientes divergen del prisma con un ángulo que depende del ángulo de corte de los prismas y de la longitud de onda de la luz. Hay disponibles prismas comerciales con un ángulo de divergencia de entre 15º y 45º.

Hay que destacar que este tipo de prisma no es un prisma polarizador en sí, sino que separa la luz previamente polarizada en dos haces.

Variantes[editar]

Sobre el diseño del prisma de Wollaston existen diversas variantes con diferencias menores que se tratan a continuación.

Prisma de Nomarski[editar]

Una variante del prisma de Wollaston es el prisma de Nomarski, llamado así en honor al físico polaco Georges Nomarski, el cual contribuyó con su invento al desarrollo de la microscopía de contraste diferencial de interferencia, también llamada microscopía de Nomarski. Es igual a un prisma de Wollaston con la particularidad de que uno de los prismas que forman la unión está cortado de manera que su eje óptico quede orientado oblicuamente con respecto a la superficie plana del prisma. Esto causa que el punto focal del haz de luz quede fuera del prisma lo que permite mayor flexibilidad, de manera que al ajustar el microscopio el prisma puede ser enfocado. es un prisma que separa la luz entrante en 2 polarizados otorgalmente este prisma se utiliza para saber la radiación de la luz entrante .

Prisma de Rochon y prisma de Sénarmont[editar]

Estos prismas reciben su nombre de los científicos franceses que los crearon, Alexis-Marie de Rochon y Henri Hureau de Senarmont. Difieren entre sí en la orientación de los ejes ópticos de los cristales y en la trayectoria de los haces divergentes. En ambos, el eje del primer cristal es paralelo al haz de luz incidente, mientras que el eje del segundo cristal es perpendicular al primero en ambos pero paralelo al plano de corte en el Rochon y girado 90º en el de Sénarmont.

Disposición del Puente de Wheatstone..

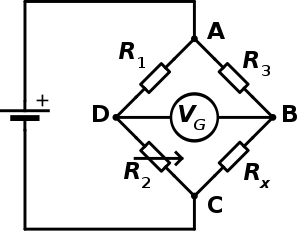
Un puente de Wheatstone es un circuito eléctrico que se utiliza para medir resistencias desconocidas mediante el equilibrio de los brazos del puente. Estos están constituidos por cuatro resistencias que forman un circuito cerrado, siendo una de ellas la resistencia bajo medida.

El físico e inventor inglés Charles Wheatstone (1802-1875) es especialmente conocido por ser el primero en aplicar el circuito eléctrico que lleva su nombre (puente de Wheatstone) para medir resistencias. En realidad había sido diseñado previamente por Samuel Hunter Christie en 1832, con lo que el papel de Wheatstone fue la mejora y popularización, a partir de 1843. También es conocido como puente de Wilton, en honor al socio de Samuel Hunter Christie, el señor Wilton de la Fuente.

Descripción[editar]

En el esquema de la derecha se tiene R_x, que es la resistencia cuyo valor se quiere determinar; R₁, R₂ y R₃ son resistencias de valores conocidos, además la resistencia R₂ es ajustable para fijar el punto de equilibro. Si la relación de las dos resistencias del brazo conocido (R₁/R₂) es igual a la relación de las dos del brazo desconocido (R₃/R_x), el voltaje entre los puntos D y B será nulo y no circulará corriente a través del galvanómetroV_G. En caso de desequilibrio, la dirección de la corriente en el galvanómetro indica si R₂ es demasiado alta o demasiado baja. El valor de voltaje de la fuente de poder (Vs) es indiferente y no afecta la medición.

Para efectuar la medida se varía la resistencia R₂ hasta alcanzar el punto de equilibrio. La detección de corriente nula se puede hacer con gran precisión mediante el galvanómetro V_G.

En condición de equilibrio siempre se cumple que:

${\displaystyle {\begin{aligned}{\frac {R_{2}}{R_{1}}}&={\frac {R_{X}}{R_{3}}}\\[4pt]\Rightarrow R_{X}&={\frac {R_{2}}{R_{1}}}\cdot R_{3}\end{aligned}}}$

Cuando el puente está construido de forma que R₃ es igual a R₁, R_x es igual a R₂ en condición de equilibrio (corriente nula por el galvanómetro).

Si los valores de R₁, R₂ y R₃ se conocen con mucha precisión, el valor de R_x puede ser determinado igualmente con precisión. Pequeños cambios en el valor de R_x romperán el equilibrio y serán claramente detectados por la indicación del galvanómetro.

De forma alternativa, si los valores de R₁, R₂ y R₃ son conocidos y R₂ no es ajustable, la corriente que fluye a través del galvanómetro puede ser utilizada para calcular el valor de R_x siendo este procedimiento más rápido que el ajustar a cero la corriente a través del medidor.

Demostración[editar]

Las direcciones de la corriente se definen arbitrariamente

Primero usamos la ley de corriente de Kirchoff (LCK) para encontrar la corriente que circula en los nodos D y B (I_G):

Nodo D:

${\displaystyle {\begin{aligned}I_{1}-I_{2}-I_{G}&=0\end{aligned}}}$

Nodo B:

${\displaystyle {\begin{aligned}I_{3}-I_{X}+I_{G}&=0\end{aligned}}}$

Luego usamos la ley de voltajes de Kirchoff (LVK) para encontrar los voltajes de las mallas ABD y BCD:

Malla ABD:

${\displaystyle {\begin{aligned}V_{3}-V_{G}-V_{1}&=0\\\Rightarrow (I_{3}\cdot R_{3})-(I_{G}\cdot R_{G})-(I_{1}\cdot R_{1})&=0\\\end{aligned}}}$

Malla BCD:

${\displaystyle {\begin{aligned}V_{X}-V_{2}+V_{G}&=0\\\Rightarrow (I_{X}\cdot R_{X})-(I_{2}\cdot R_{2})+(I_{G}\cdot R_{G})&=0\end{aligned}}}$

Cuando el puente está balanceado, entonces I_G = 0, entonces el segundo grupo de ecuaciones se puede reescribir como:

${\displaystyle {\begin{aligned}I_{3}\cdot R_{3}&=I_{1}\cdot R_{1}\\I_{X}\cdot R_{X}&=I_{2}\cdot R_{2}\end{aligned}}}$

Entonces, al dividir las ecuaciones y reordenar, se obtiene:

${\displaystyle R_{X}={{R_{2}\cdot I_{2}\cdot I_{3}\cdot R_{3}} \over {R_{1}\cdot I_{1}\cdot I_{X}}}}$

Nuevamente, si I_G = 0, entonces I₃ = I_X e I₁ = I₂. El valor deseado de R_X para lograr el equilibrio es:

${\displaystyle R_{X}={{R_{3}\cdot R_{2}} \over {R_{1}}}}$

Si conocemos los valores de las cuatro resistencias y la fuente de voltaje (V_S), y la resistencia del galvanómetro es lo suficientemente alta para que I_G sea despreciable, el voltaje en el galvanómetro (V_G) se puede determinar trabajando con el voltaje de cada divisor de tensión restándolos entre sí. La ecuación resultante es:

${\displaystyle V_{G}=\left({R_{2} \over {R_{1}+R_{2}}}-{R_{X} \over {R_{X}+R_{3}}}\right)V_{S}}$

donde V_G es el voltaje entre los nodos D y B.

Puente de Wheatstone típico

Variantes[editar]

Variantes del puente de Wheatstone se pueden utilizar para la medida de impedancias, capacitancias e inductancias.

La disposición en puente también es ampliamente utilizada en instrumentación electrónica. Para ello, se sustituyen una o más resistencias por sensores, que al variar su resistencia dan lugar a una salida proporcional a la variación. A la salida del puente, donde está el galvanómetro, (V_G) suele colocarse un amplificador.

Puente de Kelvin

El puente de Wheatstone es el fundamental, pero hay otras variantes que se pueden usar para medir diferentes tipos de resistencias cuando el puente de Wheatstone fundamental no es adecuado. Algunas de esas variantes son:

• Puente de Carey Foster, para medir pequeñas resistencias.
• Puente de Kelvin, para medir pequeñas resistencias de cuatro terminales.
• Puente de Maxwell, para medir impedancias.
• Puente de Hay para la medición de inductancias.
• Puente de Wien

Balanza electrónica[editar]

El puente de Wheatstone es ampliamente usado en balanzas electrónicas basadas en Galga extensiométrica, el objetivo de estos dispositivos es medir un voltaje de salida proporcional a la variación del peso apoyado sobre el mismo.