INGENIERÍA POR TIPO - MECÁNICA

teorema de los tres momentos o teorema de Clapeyron es una relación deducida de la teoría de flexión de vigas y usada en análisis estructural para resolver ciertos problemas de flexión hiperestática, fue demostrado por Émile Clapeyron a principios del siglo XIX.

Enunciado[editar]

Dada una viga continua de material elástico lineal sobre varios apoyos simples, los momentos flectores en tres apoyos consecutivos satisfacen la relación:¹​

(1)${\displaystyle M_{k-1}L_{k}+2M_{k}(L_{k}+L_{k+1})+M_{k+1}L_{k+1}=-6\left({\frac {\Omega _{k}D_{k}}{L_{k}}}+{\frac {\Omega _{k+1}d_{k+1}}{L_{k+1}}}\right)}$

Donde

${\displaystyle M_{k}\,}$, momento flector en el apoyo central, apoyo k-ésimo.

${\displaystyle M_{k-1}\,}$, momento flector en el apoyo a la izquierda, apoyo (k-1)-ésimo.

${\displaystyle M_{k+1}\,}$, momento flector en el apoyo a la derecha, apoyo (k+1)-ésimo.

${\displaystyle L_{k}\,}$ longitud del tramo de viga entre el apoyo (k-1)-ésimo y el apoyo k-ésimo

${\displaystyle L_{k+1}\,}$ longitud del tramo de viga entre el apoyok-ésimo y el apoyo (k+1)-ésimo.

${\displaystyle \Omega _{k},\Omega _{k+1}\,}$, área de los momentos flectores isostáticos en los tramos ${\displaystyle L_{k}\,}$ y ${\displaystyle L_{k+1}\,}$:

(2)

${\displaystyle \Omega _{k}=\int _{0}^{L_{k}}{\mathcal {M}}_{iso}^{(k)}(x)dx,\qquad \qquad \Omega _{k+1}=\int _{0}^{L_{k+1}}{\mathcal {M}}_{iso}^{(k+1)}(x)dx}$

${\displaystyle D_{k},d_{k}\,}$ son las distancias a los centroides de los diagramas de momentos flectores por la derecha y por la izquierda, el producto de estos por las áreas respectivas se puede calcular como:

(3)

${\displaystyle D_{k}={\frac {1}{\Omega _{k}}}\int _{0}^{L_{k}}x{\mathcal {M}}_{iso}^{(k)}(x)dx,\qquad \qquad d_{k}={\frac {1}{\Omega _{k+1}}}\int _{0}^{L_{k+1}}(L_{k+1}-x){\mathcal {M}}_{iso}^{(k+1)}(x)dx}$

Casos particulares[editar]

Carga continua y uniforme[editar]

Una fórmula frecuentemente empleada para tableros de puentes, viga y otros elementos con una carga uniforme es un caso particular del teorema de los tres momentos:

${\displaystyle M_{k-1}L_{k}+2M_{k}(L_{k}+L_{k+1})+M_{k+1}L_{k+1}=-\left({\frac {qL_{k}^{3}}{4}}+{\frac {qL_{k+1}^{3}}{4}}\right)}$

Cálculo de áreas y distancias[editar]

Las fórmulas integrales (2) y (3) no resultan cómodas en el caso general, sin embargo, para los casos más frecuentes de carga es posible calcular el área del diagrama de momentos isostáticos de cada tramo, y los centros de gravedad de estas áreas. Para un tramo de longitud L las magnitudes anteriores son:

Fórmulas para el área y los centros de gravedad

Tipo de carga	${\displaystyle q_{i}(x)\,}$	${\displaystyle {\mathcal {M}}_{iso}^{i}(x)}$	${\displaystyle \Omega _{i}\,}$	${\displaystyle D_{i}\,}$	${\displaystyle d_{i}\,}$
Uniforme	${\displaystyle q\,}$	${\displaystyle {\frac {q}{2}}x(L-x)}$	${\displaystyle {\frac {qL^{3}}{12}}}$	${\displaystyle {\frac {L}{2}}}$	${\displaystyle {\frac {L}{2}}}$
Puntual	${\displaystyle P\delta (x-a),\ 0\leq a\leq L\,}$	___	${\displaystyle {\frac {Pa(L-a)}{2}}}$	${\displaystyle {\frac {L+a}{3}}}$	${\displaystyle {\frac {2L-a}{3}}}$
Triangular	${\displaystyle q{\frac {x}{L}}}$	${\displaystyle {\frac {qL^{2}}{6}}\left[{\frac {x}{L}}-{\frac {x^{3}}{L^{3}}}\right]}$	${\displaystyle {\frac {qL^{3}}{24}}}$	${\displaystyle {\frac {8L}{15}}}$	${\displaystyle {\frac {7L}{15}}}$
Potencial	${\displaystyle q{\frac {x^{n}}{L^{n}}}}$	___	${\displaystyle {\frac {qL^{3}}{2(n+2)(n+3)}}}$	${\displaystyle {\frac {2L}{3}}{\frac {n+3}{n+4}}}$	${\displaystyle {\frac {L}{3}}{\frac {n+6}{n+4}}}$
Uniforme inicial	${\displaystyle {\begin{cases}q&0\leq x\leq a\\0&a\leq x\leq L\end{cases}}}$	___	${\displaystyle {\frac {qa^{2}}{12}}(3L-2a)}$	${\displaystyle {\frac {2L^{2}-a^{2}}{2(3L-2a)}}}$	${\displaystyle L-D_{i}\,}$
Uniforme centrada	${\displaystyle {\begin{cases}0&0\leq x\leq {\frac {L}{2}}-c\\q&{\frac {L}{2}}-c\leq x\leq {\frac {L}{2}}+c\\0&{\frac {L}{2}}+c\leq x\leq L\end{cases}}}$	___	${\displaystyle qc\left({\frac {L^{2}}{4}}-{\frac {c^{2}}{3}}\right)}$	${\displaystyle {\frac {L}{2}}}$	${\displaystyle {\frac {L}{2}}}$
Senoidal	${\displaystyle q_{0}\sin {\frac {\pi x}{L}}}$	${\displaystyle {\frac {q_{0}L^{2}}{\pi ^{2}}}\sin {\frac {\pi x}{L}}}$	${\displaystyle {\frac {2q_{0}L^{3}}{\pi ^{3}}}}$	${\displaystyle {\frac {L}{2}}}$	${\displaystyle {\frac {L}{2}}}$
Triangular centrada	${\displaystyle {\begin{cases}{\frac {qx}{L}}&0\leq x\leq {\frac {L}{2}}\\q-{\frac {qx}{L}}&{\frac {L}{2}}\leq x\leq L\end{cases}}}$	___	${\displaystyle {\frac {5qL^{3}}{192}}}$	${\displaystyle {\frac {L}{2}}}$	${\displaystyle {\frac {L}{2}}}$

Teorema de los dos momentos[editar]

El teorema de los dos momentos es similar pero relaciona el momento flector en dos apoyos consecutivos pero requiere que uno de ellos sea un empotramiento. Si se tiene un empotramiento a la izquierda y otro apoyo simple a la derecha, el teorema de los dos momentos establece que la relación entre ambos es:

(4a)${\displaystyle 2M_{k}+M_{k+1}=-6\left({\frac {\Omega _{k+1}d_{k+1}}{L_{k+1}^{2}}}\right)}$

Expresión que puede obtenerse como caso límite del teorema de los tres momentos anterior haciendo ${\displaystyle \Omega _{k}=0\,}$ y ${\displaystyle L_{k}\to 0\,}$.

Si el empotramiento está a la derecha y el apoyo simple a la izquierda la expresión es:

(4b)${\displaystyle M_{k-1}+2M_{k}=-6\left({\frac {\Omega _{k}D_{k}}{L_{k}^{2}}}\right)}$

Que también se obtiene de la expresión de los tres momentos haciendo ${\displaystyle \Omega _{k+1}=0\,}$ y ${\displaystyle L_{k+1}\to 0\,}$

Cálculo de reacciones[editar]

Una vez determinados los momentos hiperestáticos con ayuda del teorema de los tres momentos el cálculo de reacciones verticales en cada uno de los apoyos se puede hacer fácilmente con ayuda de la siguiente fórmula:

(5)${\displaystyle R_{k}=\overbrace {\left({\frac {M_{k-1}-M_{k}}{L_{k}}}+{\mathcal {R}}_{iso}^{(k)+}\right)} ^{izquierda(V_{k}^{-})}+\overbrace {\left({\frac {M_{k+1}-M_{k}}{L_{k+1}}}+{\mathcal {R}}_{iso}^{(k+1)-}\right)} ^{derecha(V_{k}^{+})}}$

Donde alguno de los términos anteriores debe tomarse igual a cero en el caso de los apoyos extremos por ser inexistente. Y donde:

${\displaystyle {\mathcal {R}}_{(iso)}^{(k)-}}$, es la reacción isostática en el apoyo de la izquierda del k-ésimo vano,

${\displaystyle {\mathcal {R}}_{(iso)}^{(k)+}}$, es la reacción isostática en el apoyo de la derecha del k-ésimo vano.

Obviamente:

${\displaystyle {\mathcal {R}}_{iso}^{(k)-}=\left({\frac {d{\mathcal {M}}_{iso}^{(k)}}{dx}}\right)_{x=0},\qquad {\mathcal {R}}_{iso}^{(k)+}=\left({\frac {d{\mathcal {M}}_{iso}^{(k+1)}}{dx}}\right)_{x=L_{k+1}}}$

Ejemplos[editar]

Carga continua en dos vanos[editar]

Viga continua de tres apoyos con carga continua.

Momentos flectores para viga continua de tres apoyos con carga continua.

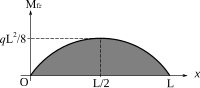
• Viga continua con carga uniforme en toda su longitud, siendo las dos longitudes iguales, en este caso, reflejado en la figura de la derecha el teorema de los tres momentos lleva a:

${\displaystyle M_{A}L+2M_{B}(L+L)+M_{C}L=-6\left({\frac {\Omega _{AB}L}{2L}}+{\frac {\Omega _{BC}L}{2L}}\right)}$

Teniendo en cuenta que en este caso ${\displaystyle \scriptstyle M_{A}=M_{C}=0}$ por ser los extremos de la viga articulados, usando la fórmula de cálculo del áreas y distancias conveniente (${\displaystyle \scriptstyle \Omega _{AB}=\Omega _{BC}=qL^{3}/12}$) y susbstituyendo en la ecuación anterior se tiene que:

${\displaystyle M_{B}=-{\frac {qL^{2}}{8}}}$

y el diagrama de momentos flectores es como el de la figura de la derecha, y viene dado por:

${\displaystyle M_{fz}(x)={\begin{cases}-{\frac {q}{8}}Lx+{\frac {q}{2}}x(L-x)&0\leq x\leq L\\-{\frac {q}{8}}L(2L-x)+{\frac {q}{2}}x(3L-x)-qL^{2}&L\leq x\leq 2L\end{cases}}}$

El máximo momento flector positivo se obtiene buscando los puntos para los cuales la derivada de la función anterior se anula ${\displaystyle \scriptstyle x=3L/8}$ y ${\displaystyle \scriptstyle x=13L/8}$ donde:

${\displaystyle M_{max}^{+}={\frac {9}{128}}qL^{2}\approx 0,0703qL^{2}}$

Esfuerzos cortantes para viga continua de tres apoyos con carga continua, los saltos en el diagrama coinciden con las reacciones.

Las reacciones en los apoyos pueden calcularse fácilmente mediante las ecuaciones (5):

${\displaystyle {\begin{cases}R_{A}={\cfrac {{\frac {-qL^{2}}{8}}-0}{L}}+{\cfrac {qL}{2}}={\cfrac {3qL}{8}}\\R_{B}=\left({\cfrac {0-{\frac {-qL^{2}}{8}}}{L}}+{\cfrac {qL}{2}}\right)+\left({\cfrac {0-{\frac {-qL^{2}}{8}}}{L}}+{\cfrac {qL}{2}}\right)={\cfrac {5qL}{8}}+{\cfrac {5qL}{8}}={\cfrac {5qL}{4}}\\R_{C}={\cfrac {{\frac {-qL^{2}}{8}}-0}{L}}+{\cfrac {qL}{2}}={\cfrac {3qL}{8}}\end{cases}}}$

Carga puntual en un vano[editar]

Viga continua de tres apoyos con carga puntual en el primer vano.

Momentos flectores para viga continua de tres apoyos con carga puntual.

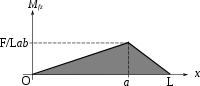
• Viga continua con carga puntual en el primer vano, siendo las dos longitudes iguales, en este caso, reflejado en la figura de la derecha el teorema de los tres momentos lleva a:

${\displaystyle M_{A}L+2M_{B}(L+L)+M_{C}L=-6\left({\frac {\Omega _{AB}L}{2L}}+{\frac {\Omega _{BC}L}{2L}}\right)}$

Teniendo en cuenta que en este caso ${\displaystyle \scriptstyle M_{A}=M_{C}=0}$ por ser los extremos de la viga articulados, usando la fórmula de cálculo del áreas y distancias conveniente (${\displaystyle \scriptstyle \Omega _{AB}=FL^{2}/8,\ \Omega _{BC}=0}$) y susbstituyendo en la ecuación anterior se tiene que:

${\displaystyle M_{B}=-{\frac {3FL}{32}}}$

El momento flector máximo se da en el primer vano y puede ser calculado como:

${\displaystyle M_{max}={\frac {M_{B}}{2}}+{\frac {FL}{4}}=-{\frac {3FL}{64}}+{\frac {FL}{4}}=+{\frac {13FL}{64}}}$

Esfuerzos cortantes para viga de tres apoyos con una carga puntual, los saltos en el diagrama coinciden con las reacciones.

y el diagrma de momentos flectores es como el de la figura de la derecha. Las reacciones en los apoyos calculadas mediante las ecuaciones de (5):

${\displaystyle {\begin{cases}R_{A}={\cfrac {{\frac {-3FL}{32}}-0}{L}}+{\cfrac {F}{2}}={\cfrac {13F}{32}}\\R_{B}=\left({\cfrac {0-{\frac {-3FL}{32}}}{L}}+{\cfrac {F}{2}}\right)+\left({\cfrac {0-{\frac {-3FL}{32}}}{L}}+0\right)={\cfrac {19F}{32}}+{\cfrac {3F}{32}}={\cfrac {11F}{16}}\\R_{C}={\cfrac {{\frac {-3FL}{32}}-0}{L}}+0=-{\cfrac {3F}{32}}\end{cases}}}$

 teorema de Maxwell-Betti, o de forma más completa, teorema de reciprocidad de Maxwell-Betti de resistencia de materiales se debe al matemático italiano Enrico Betti, quien en 1872 generalizó un teorema de Maxwell, publicado a su vez en 1864. Este teorema pertenece a una serie de teoremas energéticos, entre los que se encuentran también los teoremas de Castigliano. La importancia de los teoremas energéticos radica en su potencia en el análisis de estructuras, que se debe a su sencillez y generalidad. Este teorema es también de importancia en el planteamiento del Método de elementos de frontera.

Coeficientes de influencia[editar]

Sea un sólido elástico que se somete a un sistema de fuerzas, asumiendo las siguientes hipótesis:

• En cualquier punto del sólido, cada fuerza produce una deformación proporcional a la misma (ley de Hooke: linealidad entre tensiones y deformaciones).
• Se verifica el Principio de superposición.
• La aplicación de cualquier fuerza sobre el sólido no modifica la línea de acción de las restantes cargas aplicadas.
• Las fuerzas se aplican de manera progresiva y lineal, no dando lugar a vibraciones ni a intercambio de calor con el exterior.

Sean i y j dos puntos del sólido elástico, denominándose ${\displaystyle \Delta _{ij}\,}$ al desplazamiento del punto i al aplicar en j una fuerza ${\displaystyle F_{j}\,}$. En virtud de la primera de las hipótesis anteriormente citadas, se puede afirmar que:

${\displaystyle \Delta _{ij}\propto F_{j}\,}$

Si aplicamos un conjunto de n fuerzas sobre el sólido elástico, aplicando el principio de superposición se tendrá que el desplazamiento total del punto i será:

${\displaystyle \Delta _{i}=\Delta _{i1}+\Delta _{i2}+\cdots +\Delta _{in}\,}$

Sea ${\displaystyle \delta _{ij}\,}$ la proyección del desplazamiento del punto i sobre la dirección de la fuerza aplicada en él, ${\displaystyle F_{i}\,}$, cuando se aplica en j una carga unitaria ${\displaystyle F_{j}^{*}\,}$. Estos desplazamientos proyectados sobre la línea de acción de la fuerza son los que producen trabajo (recuérdese que el trabajo se calcula como el producto escalar de la fuerza por el desplazamiento). Definiendo de este modo ${\displaystyle \delta _{ij}\,}$, y teniendo en cuenta la proporcionalidad entre fuerzas actuantes y deformaciones enunciada anteriormente, se puede expresar el desplazamiento total del punto i proyectado en la dirección de ${\displaystyle F_{i}\,}$, de la siguiente manera:

${\displaystyle \Delta _{i}=\delta _{i1}F_{1}+\delta _{i2}F_{2}+\cdots +\delta _{in}F_{n}=\sum _{j}{\delta _{ij}F_{j}}}$

A los coeficientes ${\displaystyle \delta _{ij}\,}$ se les denomina coeficientes de influencia y representan la componente del desplazamiento que provoca una carga unitaria aplicada sobre j en el punto i, en la dirección de ${\displaystyle F_{i}\,}$.

La definición de los coeficientes de influencia se debe a Clapeyron.

Energía de deformación[editar]

Supongamos un sólido elástico inicialmente descargado, y que empezamos a cargarlo con una fuerza ${\displaystyle \alpha F_{1},\alpha \in (0,1)}$. Debido a las hipótesis expresadas anteriormente, existe proporcionalidad entre fuerzas y desplazamientos de modo que a un determinado incremento relativo de la fuerza le corresponde el mismo incremento relativo del desplazamiento, o lo que es lo mismo, la pendiente de una gráfica fuerza-desplazamientoes constante. Y por tanto, a la aplicación de una fuerza ${\displaystyle \alpha F_{1}\,}$ le corresponderá un desplazamiento ${\displaystyle \alpha \delta _{1}\,}$.

La energía de deformación acumulada durante todo el proceso de carga será igual al área que queda por debajo de la recta representada en la gráfica fuerza-desplazamiento, es decir, el área de un triángulo:

${\displaystyle W(F_{1})={\frac {1}{2}}F_{1}\delta _{1}\,}$

Si el sólido elástico no se carga con una única fuerza, sino con un conjunto de ellas, aplicando el principio de superposición se tiene:

${\displaystyle W(F_{1},F_{2},...)={\frac {1}{2}}\sum _{i}F_{i}{\delta _{i}}}$

Teniendo en cuenta lo dicho en el apartado dedicado a los coeficientes de influencia:

${\displaystyle W(F_{1},F_{2},...)={\frac {1}{2}}\sum _{i}F_{i}\sum _{j}\delta _{ij}F_{j}\,}$

Teorema de Maxwell-Betti[editar]

Sea un cuerpo elástico lineal ${\displaystyle \scriptstyle K\in \mathbb {R} ^{3}}$ sobre el que actúan dos conjuntos de fuerzas ${\displaystyle P_{i}\,}$ y ${\displaystyle Q_{j}\,}$ aplicados sobre los puntos del sólido ${\displaystyle A_{i}\,}$ y ${\displaystyle B_{j}\,}$, respectivamente. Sean:

• ${\displaystyle \lambda _{i}\,}$ los desplazamientos de los puntos ${\displaystyle A_{i}\,}$
• ${\displaystyle \mu '_{j}\,}$ los desplazamientos de los puntos ${\displaystyle B_{j}\,}$ cuando solo actúan sobre el sólido elástico las fuerzas ${\displaystyle P_{i}\,}$.

Análogamente,

• ${\displaystyle \mu _{j}\,}$ son los desplazamientos de los puntos ${\displaystyle B_{j}\,}$
• ${\displaystyle \lambda '_{i}\,}$ a los desplazamientos de los puntos ${\displaystyle A_{i}\,}$ cuando solo actúa el conjunto de fuerzas ${\displaystyle Q_{j}\,}$.

El trabajo realizado por las cargas no depende del orden de aplicación de las mismas, por lo que basta considerar dos casos:

1. Aplicamos en primer lugar el conjunto de fuerzas ${\displaystyle P_{i}\,}$, resultando la siguiente energía de deformación:

${\displaystyle W(P_{i})={\frac {1}{2}}\sum _{i}P_{i}{\lambda _{i}}}$

A continuación añadimos el conjunto ${\displaystyle Q_{j}\,}$, quedando el total de la energía de deformación como sigue:

${\displaystyle W(P_{i},Q_{j})={\frac {1}{2}}\sum _{i}P_{i}{\lambda _{i}}+{\frac {1}{2}}\sum _{j}Q_{j}{\mu _{j}}+\sum _{i}P_{i}{\lambda '_{i}}}$

El segundo término de la ecuación es debido al trabajo realizado por las fuerzas ${\displaystyle Q_{j}\,}$ sobre sus puntos de aplicación, es decir, ${\displaystyle B_{j}\,}$, mientras que el tercer término se debe a que durante la aplicación de las fuerzas ${\displaystyle Q_{j}\,}$ los puntos de aplicación de las fuerzas ${\displaystyle P_{i}\,}$ se han desplazado una cantidad ${\displaystyle \lambda '_{i}\,}$, y en consecuencia las fuerzas ${\displaystyle P_{i}\,}$ habrán realizado un trabajo. Este término no se divide por dos porque es un trabajo realizado por las fuerzas ${\displaystyle P_{i}\,}$ que han permanecido constantes durante la realización del mismo, a diferencia de los otros dos términos en los cuales el trabajo ha sido realizado durante un proceso de carga del sólido elástico, siendo de aplicación la fórmula deducida en el apartado dedicado a Energía de deformación.

2. En este segundo caso, aplicamos en primer lugar el conjunto de fuerzas ${\displaystyle Q_{j}\,}$, y a continuación añadimos el conjunto ${\displaystyle P_{i}\,}$, quedando entonces la energía de deformación como sigue:

${\displaystyle W(Q_{j},P_{i})={\frac {1}{2}}\sum _{j}Q_{j}{\mu _{j}}+{\frac {1}{2}}\sum _{i}P_{i}{\lambda _{i}}+\sum _{j}Q_{j}{\mu '_{j}}}$

Del mismo modo que en el primer caso, el tercer término se debe a que durante la aplicación de las fuerzas ${\displaystyle P_{i}\,}$ los puntos de aplicación de las fuerzas ${\displaystyle Q_{j}\,}$ se han desplazado una cantidad ${\displaystyle \mu '_{j}\,}$, y en consecuencia las fuerzas ${\displaystyle Q_{j}\,}$ realizan un trabajo.

Tal y como se ha dicho al principio, la energía de deformación no depende del orden de aplicación de las cargas por lo que igualando las expresiones obtenidas en los dos casos considerados:

${\displaystyle \sum _{i}P_{i}{\lambda '_{i}}=\sum _{j}Q_{j}{\mu '_{j}}\,}$

Esta igualdad es la que da lugar al Teorema de Maxwell-Betti, que puede enunciarse de la siguiente forma:

En un sólido elástico y lineal, siendo ${\displaystyle P_{i}\,}$ y ${\displaystyle Q_{j}\,}$ dos sistemas de cargas independientes, se establece que el "trabajo interno" realizado por el sistema de cargas ${\displaystyle P_{i}\,}$ sobre el campo de desplazamientos producido por el sistema ${\displaystyle Q_{j}\,}$ es igual al "trabajo interno" realizado por el sistema ${\displaystyle Q_{j}\,}$ sobre los desplazamientos producidos por el sistema ${\displaystyle P_{i}.\,}$ Enrico Betti

La principal consecuencia de este resultado es que los coeficientes de influencia recíprocos son iguales. En efecto, supongamos que tanto ${\displaystyle P_{i}=Q_{j}=1\,}$. Entonces el significado de ${\displaystyle \lambda '_{i}\,}$ coincide con la definición del coeficiente de influencia ${\displaystyle \delta _{ij}\,}$, mientras que ${\displaystyle \mu '_{j}\,}$ se corresponde con el coeficiente de influencia recíproco al anterior, es decir, ${\displaystyle \delta _{ji}\,}$, y por la expresión que define el Teorema de Maxwell-Betti, se tiene que:

${\displaystyle \delta _{ij}=\delta _{ji}\,}$

Este teorema es de aplicación también en el caso de que no sean fuerzas sino momentos (o incluso fuerzas y momentos) las acciones aplicadas sobre el sólido elástico, en cuyo caso los desplazamientos serán sustituidos por el ángulo de rotación correspondiente.

Casos particulares[editar]

Teorema de Maxwell[editar]

Previamente al teorema de Maxwell-Betti, en 1864, James Clerk Maxwell publicó un teorema denominado "Método de las Distorsiones o Desplazamientos Recíprocos", al que contribuyeron notablemente los trabajos de otros científicos como Mohr y Clapeyron. Se considera que este teorema da lugar al primer método de análisis para estructuras estáticamente indeterminadas. Se enuncia como sigue:

Si sobre un cuerpo elástico actúa una causa en un punto A, la deformación que se produce en otro punto del sistema B es igual a la que se produciría en A si la causa actuase en B . J. C. Maxwell

Como vemos, este teorema no es sino un caso particular del general, expresado mediante el Teorema de Maxwell-Betti, puesto que aquí únicamente se considera la actuación de una fuerza y no un conjunto de ellas.

Simetría de la matriz de rigidez[editar]

El teorema de Maxwell-Betti aplicado a una estructura lineal caracterizable mediante una matriz de rigidez, implica que la matriz de rigidez debe ser simétrica. Ya que de no serlo el estado elástico final no sería único y dependería del orden y modo de aplicación de las cargas, lo cual contradice el carácter lineal de la estructura.