Ecuaciones
La ecuación de Eyring también conocida como ecuación de Eyring–Polanyi en Cinética química relaciona la velocidad de reaccióncon la temperatura. Fue desarrollada casi simultáneamente en 1935 por Henry Eyring, M.G. Évans y Michael Polanyi. Esta ecuación es parte de la teoría del estado de transición (o bien, teoría del complejo activado) y equivale de modo trivial a la ecuación de Arrheniusobtenida empíricamente; ambas ecuaciones pueden derivarse fácilmente de la termodinámica estadística en la teoría cinética de gases.1
La forma de la ecuación de Eyring–Polanyi recuerda algo a la ecuación de Arrhenius:
donde:
- ΔG‡ es la energía libre de activación,
- kB es la constante de Boltzmann, y
- h es la constante de Planck.
Puede reescribirse como:
Para encontrar la forma lineal de la ecuación de Eyring–Polanyi se parte de:
donde:
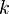 es la constante de velocidad de la ecuación de velocidad,
es la constante de velocidad de la ecuación de velocidad, es la temperatura absoluta,
es la temperatura absoluta, es la entalpía de activación,
es la entalpía de activación,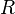 es la constante de los gases ideales,
es la constante de los gases ideales,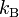 es la constante de Boltzmann,
es la constante de Boltzmann,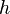 es la constante de Planck,
es la constante de Planck,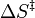 es la entropía de activación.
es la entropía de activación.
Una cierta reacción química tiene lugar a diferentes temperaturas y se determinan las velocidades de reacción. La gráfica de  versus
versus 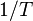 da una línea recta con pendiente
da una línea recta con pendiente  de la cual puede derivarse la entalpía de activación y de la ordenada en el origen o punto de corte con el eje de ordenadas
de la cual puede derivarse la entalpía de activación y de la ordenada en el origen o punto de corte con el eje de ordenadas  se deriva la entropía de activación.
se deriva la entropía de activación.
 versus
versus 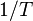 da una línea recta con pendiente
da una línea recta con pendiente  de la cual puede derivarse la entalpía de activación y de la ordenada en el origen o punto de corte con el eje de ordenadas
de la cual puede derivarse la entalpía de activación y de la ordenada en el origen o punto de corte con el eje de ordenadas  se deriva la entropía de activación.
se deriva la entropía de activación.
La ecuación de Eyring, así como la de Arrhenius, describen la relación entre temperatura y velocidad de reacción. Estrictamente hablando, la ecuación de Arrhenius sólo puede ser aplicada a la cinética de reacciones en gases.
Supongamos una reacción entre dos moléculas A y B, que reaccionan para obtener un producto C:
La velocidad de reacción estará dada por la siguiente ecuación:
Tomando en cuenta la teoría de transición de estado, A y B se encontrarán en un estado de transición inestable ( AB ‡) , antes de convertirse en C.
La velocidad de esta reacción también depende de las concentraciones de A y B, por lo tanto, esta velocidad sería descrita con la siguiente ecuación:
k‡ es una constante de estadística termodinámica, conocida como constante del estado de transición:
kB = Constante de Boltzmann [ 1.381 · 10 -23 J · K -1 ]
T = temperatura absoluta en grados Kelvin [ K ]
h = Constante de Planck [ 6.626 · 10 -34 J · s ]
Además, la concentración del estado de transición [ AB ‡ ]
Sustituyendo k‡ y [ AB ‡ ] en la ecuación 4, por las ecuaciones 5 y 6 tenemos que:
Observando la ecuación 2, podemos combinarla con la ecuación 7, y obtenemos como resultado la constante k para toda la reacción:
ΔG ‡ es la energía libre de activación, también descrita en función de entropía de activación, entalpía de activación y temperatura:
R = constante universal de los gases= 8.3145 [ J · mol -1 · K -1 ]
ΔG ‡ = energía libre de activación [ kJ · mol -1 ]
ΔS ‡ = entropía de activación [ J · mol -1 · K -1 ]
ΔH ‡ = entalpía de activación [ kJ · mol -1 ]
Combinando las expresiones 9 y 10 y despejando lnK obtenemos:
ΔS ‡ = entropía de activación [ J · mol -1 · K -1 ]
ΔH ‡ = entalpía de activación [ kJ · mol -1 ]
Combinando las expresiones 9 y 10 y despejando lnK obtenemos:
La ecuación de Eyring resulta de la sustitución de lnK en la ecuación 11 , por la ecuación 8.
La forma lineal de la ecuación de Eyring sería entonces:
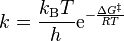
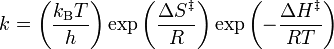
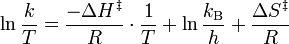
No hay comentarios:
Publicar un comentario