Ecuaciones
ecuación en diferencias es una expresión que relaciona distintas sucesiones, siendo una de ellas una sucesión desconocida.
Son similares a las ecuaciones diferenciales, sustituyendo las funciones por sucesiones.
Para su resolución suele utilizarse el método de la transformada Z
Ecuación de coeficientes lineales no constantes
La ecuación de coeficientes lineales constantes (LCCD) es una representación de un sistema lineal basada en la ecuación de la media autorregresiva.
Ambos términos de esta ecuación pueden dividirse por  , si no es cero, normalizando
, si no es cero, normalizando  la ecuación LCCD puede ser escrita
la ecuación LCCD puede ser escrita
 , si no es cero, normalizando
, si no es cero, normalizando  la ecuación LCCD puede ser escrita
la ecuación LCCD puede ser escrita
Esta forma de la ecuación LCCD es más explícita para comprobar que la salida actual ![y[{n}]\](https://upload.wikimedia.org/math/7/0/d/70d386fe8fc517002af609527dc843e1.png) se define en función de las salidas anteriores
se define en función de las salidas anteriores ![y[{n-p}]\](https://upload.wikimedia.org/math/b/7/b/b7b5966e8e057221625214b957825fbc.png) , la entrada actual
, la entrada actual ![x[{n}]\](https://upload.wikimedia.org/math/f/6/6/f669ef1c4bd8099c03a6b172887ce5eb.png) , y las entradas anteriores
, y las entradas anteriores ![x[{n-q}]\](https://upload.wikimedia.org/math/2/c/f/2cf5f29f8bd6fcecfc773b18536e913c.png) .
.
![y[{n}]\](https://upload.wikimedia.org/math/7/0/d/70d386fe8fc517002af609527dc843e1.png) se define en función de las salidas anteriores
se define en función de las salidas anteriores ![y[{n-p}]\](https://upload.wikimedia.org/math/b/7/b/b7b5966e8e057221625214b957825fbc.png) , la entrada actual
, la entrada actual ![x[{n}]\](https://upload.wikimedia.org/math/f/6/6/f669ef1c4bd8099c03a6b172887ce5eb.png) , y las entradas anteriores
, y las entradas anteriores ![x[{n-q}]\](https://upload.wikimedia.org/math/2/c/f/2cf5f29f8bd6fcecfc773b18536e913c.png) .
.
ECUACIONES
EN DIFERENCIAS .- ..................................................:http://www.dma.uvigo.es/~aurea/Tema8.pdf
Ecuaciones en diferencias .- ...............................................................:http://www.eco.uc3m.es/~rimartin/Teaching/AMATH/NOTES2SP.pdf
ecuación de Arrhenius es una expresión matemática que se utiliza para comprobar la dependencia de la constante de velocidad (o cinética) de una reacción químicacon respecto a la temperatura a la que se lleva a cabo esa reacción.1 La ecuación fue propuesta primeramente por el químico holandés J. H. van 't Hoff en 1884; cinco años después en 1889 el químico sueco Svante Arrhenius dio una justificación física y una interpretación para la ecuación. Actualmente, es vista mejor como una relación empírica.2 Puede ser usada para modelar la variación de temperatura de coeficientes de difusión, población de vacantes cristalinas, velocidad de fluencia, y muchas otras reacciones o procesos inducidos térmicamente.
Información general
Dicho de manera breve, la ecuación de Arrhenius da la dependencia de la constante de velocidad k de reacciones químicas a la temperatura T (en temperatura absoluta, tales como kelvins o grados Rankine) y la energía de activación3 Ea", de acuerdo con la expresión:1
donde:
 : constante cinética (dependiente de la temperatura)
: constante cinética (dependiente de la temperatura) : factor preexponencial o factor de frecuencia. Indica la frecuencia de las colisiones.
: factor preexponencial o factor de frecuencia. Indica la frecuencia de las colisiones. : energía de activación, expresada en J/mol.
: energía de activación, expresada en J/mol. : constante universal de los gases. Su valor es 8,3143 J·K-1·mol-1
: constante universal de los gases. Su valor es 8,3143 J·K-1·mol-1 : temperatura absoluta [K]
: temperatura absoluta [K]
Gráfico de Arrhenius
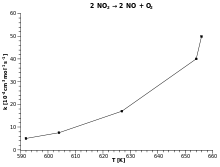
| Ejemplo: Decaimiento de dióxido de nitrógeno |
|---|
Para utilizar la ecuación de Arrhenius como modelo de regresión lineal entre las variables  y
y  , la ecuación puede ser reescrita como:
, la ecuación puede ser reescrita como:
 y
y  , la ecuación puede ser reescrita como:
, la ecuación puede ser reescrita como:
Un gráfico de Arrhenius muestra el logaritmo de las constantes cinéticas (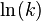 en el eje de las ordenadas en coordenadas cartesianas) graficado con respecto al inverso de la temperatura (
en el eje de las ordenadas en coordenadas cartesianas) graficado con respecto al inverso de la temperatura ( , en el eje de las abcisas). Los gráficos de Arrhenius son ocasionalmente utilizados para analizar el efecto de la temperatura en las tasas de rapidez de las reacciones químicas. Para un único proceso térmicamente activado de velocidad limitada, un gráfico de Arrhenius da una línea recta, desde la cual pueden ser determinados tanto la energía de activación como el factor preexponencial.
, en el eje de las abcisas). Los gráficos de Arrhenius son ocasionalmente utilizados para analizar el efecto de la temperatura en las tasas de rapidez de las reacciones químicas. Para un único proceso térmicamente activado de velocidad limitada, un gráfico de Arrhenius da una línea recta, desde la cual pueden ser determinados tanto la energía de activación como el factor preexponencial.
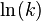 en el eje de las ordenadas en coordenadas cartesianas) graficado con respecto al inverso de la temperatura (
en el eje de las ordenadas en coordenadas cartesianas) graficado con respecto al inverso de la temperatura ( , en el eje de las abcisas). Los gráficos de Arrhenius son ocasionalmente utilizados para analizar el efecto de la temperatura en las tasas de rapidez de las reacciones químicas. Para un único proceso térmicamente activado de velocidad limitada, un gráfico de Arrhenius da una línea recta, desde la cual pueden ser determinados tanto la energía de activación como el factor preexponencial.
, en el eje de las abcisas). Los gráficos de Arrhenius son ocasionalmente utilizados para analizar el efecto de la temperatura en las tasas de rapidez de las reacciones químicas. Para un único proceso térmicamente activado de velocidad limitada, un gráfico de Arrhenius da una línea recta, desde la cual pueden ser determinados tanto la energía de activación como el factor preexponencial.
Cuando se grafica de la forma descrita anteriormente, el valor de la intersección en el eje y corresponderá a  , y la pendiente de la línea será igual a
, y la pendiente de la línea será igual a .
.
 , y la pendiente de la línea será igual a
, y la pendiente de la línea será igual a .
.
El factor preexponencial, A, es una constante de proporcionalidad que toma en cuenta un número de factores tales como la frecuencia de colisión y la orientación entre las partículas reaccionantes.
La expresión  representa la fracción de las moléculas presentes en un gas que tienen energía igual o superior a la energía de activación a una temperatura dada.
representa la fracción de las moléculas presentes en un gas que tienen energía igual o superior a la energía de activación a una temperatura dada.
 representa la fracción de las moléculas presentes en un gas que tienen energía igual o superior a la energía de activación a una temperatura dada.
representa la fracción de las moléculas presentes en un gas que tienen energía igual o superior a la energía de activación a una temperatura dada.Interpretación cinética de la ecuación de Arrhenius
Arrhenius argumentó que para que los reactivos se transformen en productos, deben primero adquirir una mínima cantidad de energía, llamada la "energía de activación" Ea. A una cierta temperatura absoluta T, la fracción de las moléculas que tiene una energía cinética mayor que Ea puede ser calculada a partir de la distribución de Maxwell-Boltzmann de la mecánica estadística, y resulta ser proporcional a 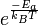 . El concepto de energía de activación explica la naturaleza exponencial de la relación, y de una forma u otra está presente en todas las teorías cinéticas.
. El concepto de energía de activación explica la naturaleza exponencial de la relación, y de una forma u otra está presente en todas las teorías cinéticas.
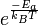 . El concepto de energía de activación explica la naturaleza exponencial de la relación, y de una forma u otra está presente en todas las teorías cinéticas.
. El concepto de energía de activación explica la naturaleza exponencial de la relación, y de una forma u otra está presente en todas las teorías cinéticas.Teoría de las colisiones
Un ejemplo viene de la "teoría de las colisiones" de las reacciones químicas, desarrollada por Max Trautz y William Lewis en los años 1916-1918. En esta teoría, se supone que las moléculas reaccionan si colisionan con una energía cinética relativa a lo largo de sus líneas de centro, que exceda Ea. Esto lleva a una expresión muy similar a la ecuación de Arrhenius.
Teoría del estado de transición
Otra expresión parecida a la ecuación de Arrhenius aparece en la "teoría del estado de transición" de las reacciones químicas, formulada por Eugene Wigner, Henry Eyring, Michael Polanyi y M. G. Evans en los años 1930s. Esto toma varias formas, pero una de las más comunes es
donde:
- ΔG‡ es la energía libre de Gibbs de activación,
- kB es la constante de Boltzmann, y
- h es la constante de Planck.
A primera vista esto luce como un exponencial multiplicado por un factor que es lineal en temperatura. Sin embargo, se debe recordar que la energía libre es por sí misma una cantidad dependiente de la temperatura. La energía libre de activación es la diferencia de un término de entalpía y un término de entropía multiplicada por la temperatura absoluta. Cuando todos los detalles son considerados, se termina con una expresión que nuevamente toma la forma de la ecuación exponencial de Arrhenius multiplicada por una función de T que varía lentamente. La forma precisa de la dependencia de temperatura depende de la reacción, y puede ser calculada usando fórmulas de la mecánica estadística, que envuelven las funciones de partición de los reactivos y del complejo activado.
Limitaciones de la idea de la energía de activación de Arrhenius
Tanto la energía de activación de Arrhenius como la constante de velocidad k son determinadas experimentalmente, y representan parámetros macroscópicos específicos de la reacción que no están relacionados de manera simple a las energías umbrales y al éxito de las colisiones individuales a nivel molecular. Considérese una colisión particular (una reacción elemental) entre las moléculas A y B. El ángulo de colisión, la energía traslacional relativa, la energía (particularmente la vibracional) interna, todos esos factores determinarán la oportunidad de que la colisión produzca una molécula AB. Las medidas macroscópicas de E y k son el resultado de muchas colisiones individuales con diferentes parámetros de colisión. Para probar las velocidades de reacción a nivel molecular, los experimentos tienen que ser realizados bajo condiciones casi colisionales y este tópico es llamado en ocasiones dinámica de reacciones moleculares.
Teoría de Arrhenius
Como ya hemos comentado en secciones anteriores en muchas reacciones, y en particular las reacciones elementales, la expresión de la velocidad puede escribirse como producto de un factor dependiente de la temperatura por otro dependiente de la composición.
| velocidad= f1(temperatura) f2(composición)velocidad= Kf2 (composición) |
Para la mayoría de estas reacciones químicas se ha encontrado que el factor dependiente de la temperatura se ajusta a la ecuación de Arrhenius
Ec. 3.1
|
donde K0 es el factor de frecuencia y Ea es la energía de activación de la reacción. Esta expresión se ajusta bien a los resultados experimentales en un amplio rango de temperaturas y se considera como una primera aproximación adecuada para el estudio del efecto de la temperatura sobre la ecuación cinética.
De la expresión anterior podemos ver que a temperatura constante cuanto mayor es la Ea, más pequeña será la constante de velocidad y por lo tanto más lenta será la velocidad de reacción. Por el contrario velocidades de reacción rápida tendrán una Ea pequeña.
La expresión de Arrhenius se obtuvo originariamente a partir de consideraciones termodinámicas. Para una reacción elemental cuyas velocidades sean lo suficientemente rápidas y así alcanzar un equilibrio dinámico, la ecuación de van´t Hoff enuncia que
Ec. 3.2
|
En el caso de la reacción
con K1 y K1´ siendo las constantes de velocidad directa e inversa respectivamente. Las constantes de velocidad se relacionan entre sí por medio de la expresión
Ec. 3.3
|
Sustituyendo la Ec. 3.3 en la Ec. 3.2 se obtiene
Ec. 3.4
|
El hecho de que la diferencia de derivadas sea igual a sugiere la posibilidad de que cada una de estas derivadas pueda igualarse a un término de la forma
Ec. 3.5
|
Ec. 3.6
|
donde
(Ei: nivel energético)
Integrando cualquiera de las ecuaciones anteriores (Ec. 3.5 o Ec. 3.6) y haciendo que la constante de integración sea ln K0, se obtiene un resultado en forma de la ecuación de Arrhenius
Ec. 3.7
|
Otra posible derivación de la expresión de Arrhenius está basada en el concepto de estado de transición o activado, que es uno de los postulados de la teoría del estado de transición que estudiaremos más adelante. Supongamos que el producto C de la reacción
sólo esté formado por la descomposición de una forma activada de los reactantes A y B, a la que denominaremos (AB)*. La reacción tiene lugar por medio de las reacciones elementales siguientes:
Si la primera etapa es comparativamente mucho más rápida que la segunda etapa la concentración de (AB)* la podremos expresar de la forma
Ec. 3.8
|
donde K* es la constante de equilibrio para la formación de (AB)*. Utilizando la Ec. 3.8, la velocidad de reacción (velocidad de formación de C) queda dada por la velocidad de la etapa de descomposición de primer orden
Ec. 3.9
|
Si integramos la ecuación de van´t Hoff (Ec. 3.2), reemplazando K por K*, el resultado será
Ec. 3.10
|
siendo I la constante de integración. Combinado las Ec. 3.9 y 3.10 se obtiene
Ec. 3.11
|
Si comparamos esta última expresión con la expresión de Arrhenius, Ec. 3.1 podemos escribir:
Ec.3.12
|
Puesto que es la energía requerida para formar el estado activado (AB*) a partir de A y B, es la expresión de Boltzmann para la fracción de moléculas que tienen una energía en exceso de la energía promedio. Esto le da un significado a la energía de activación E de la ecuación de Arrhenius. En la Fig. 3.1 se muestra que este valor es la barrera de energía que debe superarse para formar (AB)* y finalmente el producto C.
Fig 3.1
Si consideramos la reacción
es de segundo orden en ambas direcciones. Para que las moléculas de H2 y I2 reaccionen dando IH, es necesario que antes choquen. Una cierta fracción de estas moléculas adquirirá la energía de activación suficiente y formará moléculas activadas, que en este caso serán de la forma indicada por la Fig. 3.2. En la misma figura se indica la naturaleza indefinida de los enlaces del complejo activado por medio de lineas de puntos. En esta situación el complejo activado puede dar lugar a productos o bien se pueden formar de nuevo los reactivos de partida.
La teoría de Arrhenius es el primer paso para dar una interpretación molecular de los procesos que ocurren en una reacción química. Sin embargo, la teoría no conduce a resultados cuantitativos, por lo que se han desarrollado otras, que basándose en las ideas de Arrhenius, pueden predecir en casos sencillos los resultados experimentales.
![\sum_{p=0}^{N}y[n-p]\alpha_{p} = \sum_{q=0}^{M}x[n-q]\beta_{q}\](https://upload.wikimedia.org/math/d/c/5/dc56f77192c3d0d2dafc3bf76362f500.png)
![y[n] = \sum_{q=0}^{M}x[n-q]\beta_{q} - \sum_{p=1}^{N}y[n-p]\alpha_{p}\](https://upload.wikimedia.org/math/6/4/7/647e9803e9dbc3ac6e7b4b481b2ef995.png)




No hay comentarios:
Publicar un comentario