Ecuaciones
conjunto de soluciones es el conjunto de valores que satisfacen una ecuación, una inecuación, un sistema de ecuaciones, o uno de inecuaciones. Es un subconjunto de los valores «permitidos» a las incógnitas.1
El conjunto de soluciones puede tener un solo elemento, varios (incluso infinitos, por ejemplo en una identidad) o ninguno (el conjunto vacío).
Definición
Dada una aplicación  , la expresión
, la expresión 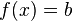 determina una ecuación, en tanto consideremos a x como una indeterminada que pertenece al conjunto A.
determina una ecuación, en tanto consideremos a x como una indeterminada que pertenece al conjunto A.
 , la expresión
, la expresión 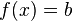 determina una ecuación, en tanto consideremos a x como una indeterminada que pertenece al conjunto A.
determina una ecuación, en tanto consideremos a x como una indeterminada que pertenece al conjunto A.
|
El conjunto solución está constituido por todos los 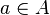 determinados que cumplen la ecuación, es decir, aquellos para los cuales
determinados que cumplen la ecuación, es decir, aquellos para los cuales 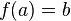 .
.
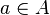 determinados que cumplen la ecuación, es decir, aquellos para los cuales
determinados que cumplen la ecuación, es decir, aquellos para los cuales 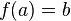 .
.
De modo análogo puede definirse el conjunto solución para las inecuaciones, pero sólo bajo ciertas condiciones. Si  denota al conjunto de soluciones de la ecuación
denota al conjunto de soluciones de la ecuación 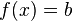 , la inecuación
, la inecuación  tiene como solución a
tiene como solución a  , es decir, el complemento de
, es decir, el complemento de  .
.
 denota al conjunto de soluciones de la ecuación
denota al conjunto de soluciones de la ecuación 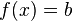 , la inecuación
, la inecuación  tiene como solución a
tiene como solución a  , es decir, el complemento de
, es decir, el complemento de  .
.
Para otros tipos de desigualdades, como las relaciones < o >, se requiere que A y B sean conjuntos parcialmente ordenados con una relación de orden equivalente. Así, si  representa una relación de este tipo, la solución de
representa una relación de este tipo, la solución de 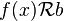 está constituida por los elementos de A que cumplen esa relación.
está constituida por los elementos de A que cumplen esa relación.
 representa una relación de este tipo, la solución de
representa una relación de este tipo, la solución de 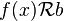 está constituida por los elementos de A que cumplen esa relación.
está constituida por los elementos de A que cumplen esa relación.Ejemplos
- Para
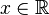 ,
,  tiene por conjunto de soluciones
tiene por conjunto de soluciones 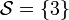 (tiene una solución).
(tiene una solución). - Para
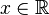 ,
,  tiene por conjunto de soluciones
tiene por conjunto de soluciones  (no tiene soluciones).
(no tiene soluciones). - Para
 ,
,  tiene por conjunto de soluciones
tiene por conjunto de soluciones 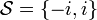 (tiene dos soluciones).
(tiene dos soluciones). - Para
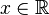 ,
,  tiene por conjunto de soluciones
tiene por conjunto de soluciones ![\mathcal{S}= [-3, 3]](https://upload.wikimedia.org/math/b/1/2/b1256ae8b08eaf78ace057350323b909.png) (un intervalo).
(un intervalo). - Para
 , la ecuación en dos variables
, la ecuación en dos variables  tiene como conjunto de soluciones
tiene como conjunto de soluciones  , que geométricamente puede representarse como una recta en el plano euclídeo,2 con un «agujero» en el punto
, que geométricamente puede representarse como una recta en el plano euclídeo,2 con un «agujero» en el punto  . Este problema aparece porque
. Este problema aparece porque  es una expresión que conduce a una división por cero en la ecuación.
es una expresión que conduce a una división por cero en la ecuación. - Para f una función real que cumple
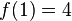 , la ecuación diferencial ordinaria
, la ecuación diferencial ordinaria 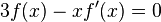 tiene como conjunto de soluciones
tiene como conjunto de soluciones  .
.
Conjuntos solución para ecuaciones
El conjunto que contiene todas las soluciones de una ecuación es llamado el conjunto solución para esa ecuación.
Si una ecuación no tiene soluciones, escribimos  para el conjunto solución.
para el conjunto solución.  significa el conjunto nulo (o conjunto vacío).
significa el conjunto nulo (o conjunto vacío).
Ecuación
|
Conjunto solución
|
3x + 5 = 11
|
{2}
|
x2 = x
|
{0, 1}
|
x + 1 = 1 + x
|
R (el conjunto de todos los números reales)
|
x + 1 = x
|
Conjuntos solución para desigualdades
Los conjuntos solución para desigualdades son a menudo conjuntos infinitos; no podemos enlistar todos los números. Así, usamos una notación especial.
Ejemplo:
Resuelva la desigualdad
x + 2  –3.
–3.
Restando 2 en ambos lados, obtenemos la desigualdad equivalente
x  –5.
–5.
Así, el conjunto solución es
{x | x  –5}.
–5}.
La desigualdad de Fisher (Fisher's inequality en inglés) es una condición necesaria por la existencia de un diseño de bloque incompleto balanceado lo cual satisface ciertas condiciones prescritas en la matemática combinatoria. Delineado por Ronald Fisher, un genetista de las poblaciones y estadístico, se preocupó por los diseños experimentales y estudiaba la diferencia entre variasvariedad de las plantas, cada una abajo de un número de diferentes condiciones de cultivo, que se llaman bloques.
Asume:
- v es el número de variedades de plantas;
- b es el número de bloques.
Se exigió que:
- k variedades distintas están en cada bloque, k < v; no hay variedad que ocurra dos veces en algún bloque;
- dos variedades ocurran juntas en exactamente λ bloques;
- cada variedad ocurra en exactamente r bloques.
La desigualdad de Fisher dice que:
-
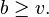
Prueba
Asume que la matriz de incidencia M sea una v×b matriz definida para que Mi,j es 1 si elemento i está en bloque j y 0 no. Luego B=MMT es una matriz v×v tal que Bi,i= r y Bi,j = λ por i ≠ j. Dad que r ≠ λ, det(B) ≠ 0, así rango(B) = v; por otra parte, rango(B) = rango(M) ≤ b, así v ≤ b.Generalidades
La desigualdad de Fisher es válido por clases más generalizadas de diseño. Un «diseño balanceado que ocurre en pares» es un grupo X junto con una familia de subconjuntos de X (lo cual no hace falta tener el mismo tamaño ni contener repeticiones) tal que cada par de elementos distintos de X se contiene exactamente en λ (un entero positivo) conjuntos. El grupo X se pueda hacer uno de los subconjuntos, y si todos los subconjuntos son de X, el «diseño balanceado que ocurre en pares» se llama trivial. El tamaño de X is v y el número de otros subconjuntos en la familia, contado con multiplicidad, es b.Teorema: Por cualquier «diseño balanceado que ocurre en pares» que no es trivial, v ≤ b.1Este resultado generaliza el teorema de Erdős-De Bruijn:Por un PBD con λ = 1 que no tenga bloques de tamaño 1 o tamaño v, v ≤ b, con igualdad si el «diseño balanceado que ocurre en pares» sea un plano proyectivo.- El modelo de KRUTILLA J. y FISHER A. (1985) tiene, como el de los EMS, visto en el apartado anterior, el objetivo de acotar un valor para los beneficios de la preservación, pero va mucho más allá.Parte de la inecuación Bd-Cd-Bp>0, vista anteriormente, y que ahora escribimos B-C-P>0 para que nos facilite el expresar esas variables en distintos periodos, pero extendida a un número indefinido de periodos y aplicando una tasa de descuento variable.Hipótesis del modelo:
- Los costes –distintos de los de preservación- se desembolsan en el período inicial y se toman como unidad
- Se supone que los benéficos de la preservación aumentarían con el paso del tiempo a una tasa σ, ya que:
- Se trata de bienes superiores Þ con elasticidad renta mayor que la unidad
- La oferta de esos bienes presumiblemente caerá en el futuro
- Se supone que los beneficios convencionales derivados del proyecto caen a una tasa μ, debido a la obsolescencia progresiva previsible por el cambio tecnológico.
Únicamente debe fijarse entonces el B del periodo inicial, esto es, 'Bo', y realizar el análisis de sensibilidad para la variable P en el momento inicial, esto es, 'Po'.Se tiene distintas expresiones del valor actual neto VAN que depende de la variable tasa de descuento 'i'. En el gráfico siguiente se han tomado dos valores para Po. (Ver simulación en Banco de prácticas sobre el modelo de Fisher-Krutilla de la sección 'Descarga')Vemos que para el Po más bajo existe un intervalo de 'i' para que que el VAN es positivo. Para el Po más alto el VAN es negativo cualquiera que sea 'i'. Existirá, entonces, un único valor para Po, digamos Po*, para el cual la curva VAN será tangente al eje de abscisas, es decir, únicamente par un 'i' el VAN es no negativo. Esa es la acotación de Po.La autoridad ambiental deberá demostrar que el valor de los beneficios ambientales actuales es inferior a Po*. caso contrario el proyecto de desarrollo no debe realizarse de ninguna manera, pues arrojaría un VAN negativo cualquiera que fuese la tasa de descuento que se aplicase.Además, si la autoridad ambiental demuestra que el valor de Po es inferior a Po*, todavía deberá demostrar que no existe otro proyecto en que destinar los fondos de mayor VAN para un 'i' dentro del intervalo factible.Puede verse el desarrollo matemático completo en: Formulación matemática de modelo de Krutilla-FisherSe llega a la desigualdad de Porter:a partir de la cual se puede calcular Po*, es decir aquél para que exista intervalo factible de 'i' está constituido por un único punto. - Resolución
No hay comentarios:
Publicar un comentario