domingo, 8 de noviembre de 2015

Álgebra

Ecuaciones

ecuación paramétrica permite representar una curva o superficie en el plano o en el espacio, mediante valores arbitrarios o mediante una constante, llamada parámetro, en lugar de mediante una variable independiente de cuyos valores se desprenden los de la variable dependiente. Un ejemplo simple de la cinemática, es cuando se usa un parámetro de tiempo (t) para determinar la posición y la velocidad de un móvil.

Puede describirse una hélice con la ecuación paramétrica f(t) = (5\cos(t), 5\sin(t), t/5). Al variar el valor de t, se obtienen los distintos puntos de la curva.

Descripción

En el uso estándar del sistema de coordenadas, una o dos variables (dependiendo de si se utilizan dos o tres dimensiones respectivamente) son consideradas comovariables independientes, mientras que la restante es la variable dependiente, con el valor de ésta siendo equivalente al de la imagen de la función cuando los restantes valores son sus parámetros. Así por ejemplo la expresión de un punto cualquiera (x, y) equivale a la expresión (x, f(x)).
Esta representación tiene la limitación de requerir que la curva sea una función de x en y, es decir que todos los valores x tengan un valor y sólo un valor correspondiente en y. No todas las curvas cumplen con dicha condición. Para poder trabajar con la misma como si se tratara de una función, lo que se hace es elegir un dominio y una imagen diferentes, en donde la misma sí sea función. Para hacer esto, tanto x como y son considerados variables dependientes, cuyo resultado surge de una tercera variable (sin representación gráfica) conocida como «parámetro».

Ejemplo

Sea 3x - 2y - 5 = 0 la ecuación general de una recta, entonces caben la ecuaciones paramétricas:1
\begin{cases} x=& 2t +5 \\ y= & 3t+5 \end{cases}

Otro ejemplo para aclarar

Cuando se toma un intervalo en el ejet, los puntos c(t) = (t, t2) describen una parábola.
Dada la ecuación y = x^2, una parametrización tendrá la forma \begin{cases} x = u (t) \\ y = v (t) \end{cases}
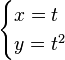
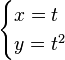
Una parametrización posible sería \begin{cases} x = t \\ y = t^2 \end{cases}
Se debe destacar que para cada curva existen infinitas parametrizaciones posibles. Una en donde x e y equivaliesen a 2U y 4U^2sería igualmente válida. La diferencia sería que, para encontrar un punto determinado (a, b) de la curva, el valor del parámetro sería diferente en cada caso. Con el ejemplo dado, el punto (2, 4) de la curva aparecería en la primera parametrización cuando t = 2, y en el segundo cuando U = 1.

Curvas notables

Circunferencia

Ecuación paramétrica de la circunferencia goniométrica. La variable t es el ángulo y sus puntos son: (x, y) = (cost, sint).
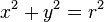
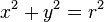
Una circunferencia con centro en el origen de coordenadas y radio r verifica que x^2 + y^2 =r^2
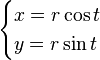
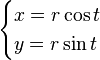
Una expresión paramétrica es \begin{cases} x = r \cos t \\ y = r \sin t \end{cases}

Elipse

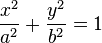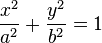Una elipse con centro en el origen de coordenadas y que se interseque con el eje x en a y -a, y con el eje y en b y -b, verifica que \frac{x^2}{a^2} + \frac{y^2}{b^2} =1.
Una expresión paramétrica es \begin{cases} x = a \cos t \\ y = b \sin t \end{cases}.

Otras curvas

Diferentes figuras variando k
La expresión paramétrica de una función permite la construcción de una gran variedad de formas, simplemente variando alguna constante. A continuación se describe la función paramétrica:
x = (a - b) \cos(t)\ + b \cos(t ((a / b) - 1))
y = (a - b) \sin(t)\ - b \sin(t ((a / b) - 1))
Dependiendo del ratio k = a/b pueden obtenerse formas muy diversas.
En esta otra función se puede ver una gran variedad de formas en función de los exponentes j y k, variando los paràmetrosa,b,c y d.
x = \cos(a t) - \cos(b t)^j
y = \sin(c t) - \sin(d t)^k
A continuación ejemplos para j=3 k=3 y j=3 k=4.
  • j=3 k=3
    •  
  • j=3 k=3
    •  
  • j=3 k=4
    •  
  • j=3 k=4
    •  
  • j=3 k=4

A continuación se describe otra función donde puede obtenerse una gran diversidad de formas, variando el valor de las constantes: i,j,a,b,c,d,e.
x = i \cos(a t) - \cos(b t) \sin(c t)
y = j \sin(d t) - \sin(e t)
  • i=1 j=2
Las ecuaciones paramétricas a menudo describen bellas figuras.
  • Representación gráfica de tres funciones paramétricas.
    •  
  • Representación gráfica de dos funciones paramétricas.
    •  
  • Representación gráfica de dos funciones paramétricas.

Representación paramétrica de una curva

La representación paramétrica de una curva en un espacio n-dimensional consiste en n funciones de una variable t que en este caso es la variable independiente oparámetro (habitualmente se considera que t es un número real y que los puntos del espacio n-dimensional están representados por n coordenadas reales), de la forma e_i=f_i(t),\,f_i:[a,b] \rightarrow {\mathbb R}, donde ei representa la i-ésima coordenada del punto generado al asignar valores del intervalo [a, b] a t. Por ejemplo, para representar una curva en el espacio se usan 3 funciones x = x(t), y = y(t), z = z(t)
Es común que se exija que el intervalo [a, b] sea tal que a cada punto a \leq t < b le corresponda un punto distinto de la curva; si las coordenadas del punto obtenido al hacer t = a son las mismas del punto correspondiente a t = b la curva se denomina cerrada.
Se dice que un punto de la curva correspondiente a un valor t del intervalo es un punto ordinario si las derivadas de las funciones paramétricas existen en y son continuas en ese punto y al menos una es distinta de 0. Si un arco de curva está compuesto solamente de puntos ordinarios se denomina suave.
Es común resumir las ecuaciones paramétricas de una curva en una sola ecuación vectorial
\vec{r}(t) = \sum_{i=1}^n f_i(t)\hat{e}_i = f_1(t)\hat{e}_1 + f_2(t)\hat{e}_2 + \dots + f_n(t)\hat{e}_n,
donde êi representa al vector unitario correspondiente a la coordenada i-ésima. Por ejemplo, las funciones paramétricas de un círculo unitario con centro en el origen son x = cos t, y = sen t. Podemos reunir estas ecuaciones como una sola ecuación de la forma
\vec{r}(t) = \cos(t)\hat{i} + \sin(t)\hat{j}.


Ecuacion Parametrica De La Linea Recta

Ecuación paramétrica de la línea recta
La recta constituye una parte fundamental de las matemáticas. Existen numerosas formas de representar una recta, lo que incluye tanto laforma paramétrica como la vectorial. Un espacio tridimensional puede ser utilizado para determinar una ecuación vectorial que denote una línea recta. El parámetro es sencillamente una variable cuyo objetivo principal es describir una relación particular con la ayuda de los parámetros. Por tanto, una ecuación paramétrica es una ecuación que está basada en una variable en particular. Una ecuación paramétrica, en términos generales, se conoce también como representación paramétrica. Ejemplo: Considere la ecuación x = 2 + 3t. En esta ecuación, t denota el parámetro y la ecuación se conoce como ecuación paramétrica en términos de t.
Si así consta, por lo general, las ecuaciones de la forma x = x0 + ta; y = y0 + tb; z = z0 + tc representan las ecuaciones paramétricas delínea recta. Para conseguir un punto particular en la recta, todo lo que tenemos que hacer es tomar el valor de t de cualquiera de las ecuaciones e insertarlo en otra ecuación. Como resultado, obtenemos las coordenadas reales de un punto determinado en la recta.
Consideremos un ejemplo con el fin de encontrar una ecuación paramétrica para una recta entre los puntos (−1, 3) y (1, 1).
Paso 1: De los puntos dados en el enunciado, elija uno como punto inicial. Consideremos a (−1, 3) como punto inicial.
Paso 2: Ahora, tomemos las coordenadas x para los rangos indicados. Es posible observar que −1 está a 2 unidades de distancia del 1. Por tanto, x = −1 + 2t
Paso 3: Del mismo modo, teniendo en cuenta las coordenadas y para los rangos indicados, es posible ver que el 3 está a −2 unidades de distancia del1. Por tanto, y = 3 - 2t.
Por consiguiente, las ecuaciones paramétricas para la recta entre los puntos (−1, 3) y (1, 1) son x = −1 + 2t e y = 3 - 2t. Otra forma de ecuación paramétrica en el campo del cálculo vectorial se denomina ecuación vectorial. El cálculo de la ecuación vectorial se basa en el concepto del cálculo de la ecuación paramétrica.
Por ejemplo: Suponga que queremos encontrar una ecuación vectorial para una línea entre los puntos (−1, 3) y (1, 1).
Se procede de la siguiente manera:
Paso 1: De los puntos dados en el enunciado, elija uno como punto inicial. Consideremos a (−1, 3) como punto inicial.
Paso 2: Un vector de dirección es calculado. Es el vector que muestra movimiento desde el punto inicial hasta el punto final. Ahora, con el fin de alcanzar al punto (1, 1), debemos mover a x e y a 2 y −2 unidades, respectivamente. Por tanto, el vector de dirección viene a ser (2, −2).
Paso 3: Por consiguiente, la ecuación vectorial toma la forma de: (−1, 3) + (2, −2) t.
La principal diferencia entre la ecuación paramétrica y la vectorial de la recta es el hecho de que con la ayuda de la ecuación vectorial de la recta, la forma del vector es conocida, mientras que la forma paramétrica ayuda a conocer las coordenadas reales del punto.

Publicado por en

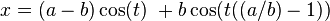
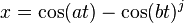
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)