Electrodinámica
La corriente de Foucault (corriente parásita también conocida como "corrientes torbellino", o eddy current en inglés) es un fenómeno eléctrico descubierto por el físico francés Léon Foucault en 1851. Se produce cuando un conductor atraviesa un campo magnético variable, o viceversa. El movimiento relativo causa una circulación deelectrones, o corriente inducida dentro del conductor. Estas corrientes circulares de Foucault crean electroimanescon campos magnéticos que se oponen al efecto del campo magnético aplicado (ver Ley de Lenz). Cuanto más fuerte sea el campo magnético aplicado, o mayor la conductividad del conductor, o mayor la velocidad relativa de movimiento, mayores serán las corrientes de Foucault y los campos opositores generados.
En los núcleos de bobinas y transformadores se generan tensiones inducidas debido a las variaciones de flujo magnético a que se someten aquellos núcleos. Estas tensiones inducidas son causa de que se produzcan corrientes parásitas en el núcleo (llamadas corrientes de Foucault), que no son óptimas para la buena eficiencia eléctrica de éste.
Las corrientes de Foucault crean pérdidas de energía a través del efecto Joule. Más concretamente, dichas corrientes transforman formas útiles de energía, como la cinética, en calor no deseado, por lo que generalmente es un efecto inútil, cuando no perjudicial. A su vez disminuyen la eficiencia de muchos dispositivos que usan campos magnéticos variables, como los transformadores de núcleo de hierro y los motores eléctricos. Estas pérdidas son minimizadas utilizando núcleos con materiales magnéticos que tengan baja conductividad eléctrica (como por ejemplo ferrita) o utilizando delgadas hojas de acero eléctrico, apiladas pero separadas entre sí mediante un barnizaislante u oxidadas tal que queden mutuamente aisladas eléctricamente. Los electrones no pueden atravesar la capa aislante entre los laminados y, por lo tanto, no pueden circular en arcos abiertos. Se acumulan cargas en los extremos del laminado, en un proceso análogo al efecto Hall, produciendo campos eléctricos que se oponen a una mayor acumulación de cargas y a su vez eliminando las corrientes de Foucault. Cuanto más corta sea la distancia entre laminados adyacentes (por ejemplo, cuanto mayor sea el número de laminados por unidad de área, perpendicular al campo aplicado), mayor será la eliminación de las corrientes de Foucault y, por lo tanto, menor el calentamiento del núcleo.
A medida que la placa metálica circular se mueve a través de una pequeña región de campo magnéticoconstante entrante a la imagen, las corrientes de Foucault son inducidas en ésta. La dirección de esas corrientes está determinada por la Ley de Lenz.
Orígenes de las corrientes de Foucault
Si hacemos oscilar un péndulo constituido por una placa de cobre entre los polos de un electroimán, se observará que se va frenando hasta pararse por completo, produciéndose este efecto más rápidamente cuanto mayor sea la intensidad del campo. Al tratarse de una placa de cobre, material no magnético, el frenado del péndulo no es debido a la atracción de los polos del imán.
Lo que sucede es que en la placa, al cortar el flujo entre las piezas polares, se induce una fuerza electromotriz, según predice la ley de Lenz. Como el cobre es un buen conductor y la placa ofrece una gran sección al paso de la corriente, su resistencia óhmica es pequeña y las corrientes inducidas intensas. Estas corrientes se oponen a la acción del origen que las produce, esto es, la propia oscilación del péndulo, por tanto, actúan de freno.
La energía cinética del péndulo en movimiento, por el principio conservación, se transforma en calor por el efecto Joule.
Otros ejemplos claros donde aparecen este tipo de corrientes inductoras lo podemos observar en la mayoría de maquinaria eléctrica, dinamos, motores de corriente continua, alternadores, transformadores y en cualquier máquina donde exista un flujo de inducción.
En general, las corrientes de Foucault son indeseadas, ya que representan una inútil disipación de energía en forma de calor.
Aplicaciones
Eléctricas
Las corrientes de Foucault son usadas para aumentar el efecto en convertidores de movimiento a electricidad como en los generadores eléctricos y los micrófonos dinámicos. También pueden ser usados para inducir un campo magnético en latas de aluminio, lo que permiten que éstas sean fácilmente separables de otros elementos reciclables. Los superconductores permiten una conducción perfecta, sin pérdidas, que crean corrientes de Foucault iguales y opuestas al campo magnético externo, permitiendo de esta manera la levitación magnética. Por la misma razón, los campos magnéticos dentro de un medio superconductor serán exactamente cero, independientemente del campo externo aplicado.
Una de las aplicaciones prácticas de las corrientes de Foucault es la utilizada en los medidores de consumo eléctrico, donde el disco corta líneas de fuerza, al girar, accionado por el campo de un imán. Las corrientes, que se producen en el disco, generan una fuerza opuesta a la que acciona. Este frenado de corrientes de Foucault permite calibrar los contadores, modificando la posición del imán. Este mismo dispositivo sirve para el ajuste de fin de velocidad de los gira discos y el amortiguamiento de los instrumentos de medida.
Algunos tacómetros tienen un imán que gira a la velocidad que se trate de medir frente a un disco metálico móvil. Las acciones electromagnéticas, debidas a las corrientes de Foucault, lo accionan en sentido de rotación del imán. Gracias a un muelle de retorno, se consigue inmovilizar el disco en una posición de equilibrio, que es función de la velocidad del imán.
Las corrientes de Foucault se emplean aún en ensayos no destructivos para detectar discontinuidades superficiales y medirconductividad eléctrica en metales no magnéticos.
Mecánicas
Las corrientes de Foucault son usadas para frenar al final de algunas montañas rusas. Este mecanismo no tiene ningún desgaste mecánico y produce una precisa fuerza de frenado. Típicamente, pesadas placas de cobre extendiéndose desde el carro son movidas entre pares de imanes permanentes muy potentes. La resistencia eléctricaentre las placas genera un efecto de arrastre análogo a la fricción, que disipa la energía cinética del carro.
Efecto de frenado
Aunque la pérdida de energía útil resulta casi siempre indeseable, a veces tiene algunas aplicaciones prácticas. Una de ellas es en algunos trenes y vehículos pesados, como autocares y camiones, cuyos frenos se actúan a base de inducir corrientes de Foucault (eddy current brake). Durante el frenado, las llantas de metal en las ruedas están expuestas al campo magnético de un electroimán, que genera corrientes de Foucault en los núcleos y llantas de las ruedas. Las corrientes de Foucault encuentran resistencia mientras circulan a través del metal, y disipan energía en forma de calor, haciendo que las ruedas disminuyan su velocidad. Cuanto más rápido giren las ruedas, más fuerte será el efecto, resultando que a medida que el tren disminuye su velocidad, también lo hará la fuerza de frenado, consiguiéndose un frenado suave proporcional a la velocidad de las ruedas.
Si colocamos un disco de aluminio, que gira de forma libre, frente a un imán, el campo magnético producido por el imán reduce sensiblemente la velocidad de rotación del disco, es decir, produce un par de frenado proporcional a la velocidad del disco. Este efecto de frenado es también debido a las corrientes de Foucault, y se aplica en numerosos aparatos de medida, como por ejemplo, en los vatihorímetros o contadores de energía eléctrica. Hay que puntualizar que esta acción de frenado sólo se manifiesta en planos perpendiculares a las líneas de inducción, ya que los circuitos abrazan la mayor parte del flujo, experimentando el máximo efecto de las variaciones cuando está de forma perpendicular.
Efectos colaterales
Las corrientes de Foucault son la causa principal del efecto pelicular en conductores que transportan corriente alterna.
Pérdidas de energía
Las corrientes de Foucault, como ya se ha comentado, tienen por efecto transformar parte de la energía en calor. Dicho calor producido en la masa metálica sólo se utiliza en los hornos eléctricos de alta frecuencia, por lo que, en general, supone una pérdida de energía. Para el estudio de estas pérdidas, consideraremos a una chapa de longitud  , anchura
, anchura  y grosor
y grosor  , sometida un campo variable de valor:
, sometida un campo variable de valor:
 , anchura
, anchura  y grosor
y grosor  , sometida un campo variable de valor:
, sometida un campo variable de valor:
donde ω es la pulsación y Bm la inducción máxima.
En esta circunstancia el flujo a través de la superficie de dicha espira es:
Donde S es la superficie que atraviesa el flujo, cuyo valor es
Por lo tanto es posible escribir la ecuación anterior en la forma:
Por otra parte, sabemos que la fem inducida en la espira es:
Derivando se tiene:
Si tomamos en la chapa una espira diferencial, su resistencia será
y despreciando 2x frente a 2b, escribiremos:
La potencia en la espira será,
siendo Eef la tensión eficaz, cuyo valor en función del máximo, Em, es
Por lo tanto la potencia perdida será:
Y la potencia total perdida a consecuencia de las corrientes de Foucault:
< Si reemplazamos ahora ω por  , se obtiene
, se obtiene
 , se obtiene
, se obtiene
o, lo que es lo mismo
en donde 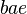 , es el volumen de la carga.
, es el volumen de la carga.
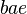 , es el volumen de la carga.
, es el volumen de la carga.
De todo lo expuesto se deduce que las pérdidas en vatios por metro cúbico debidas a las corrientes de Foucault serán:
Dado el carácter perjudicial de las corrientes de Foucault, por los motivos ya apuntados, es necesario tomar las siguientes precauciones:
-
- a) Todas las masas metálicas sometidas a variaciones de inducción deben ser laminadas y colocadas en paquetes paralelos. De esta forma se evita el recorrido de las corrientes de Foucault engendradas en planos perpendiculares a los flujos.
-
- b) Los remaches y tornillos que unen las chapas no deben cerrar circuitos conductores que abracen flujo variable.
-
- c) Los soportes metálicos de las bobinas han de ser cortados por medio de una incisión paralela a las líneas de inducción, o bien utilizar sustancias no conductoras.
Reducción de las corrientes
Si el ejemplo del péndulo lo repetimos, modificando la estructura de las placas de cobre, es decir, hendimos la pieza de forma vertical con numerosos cortes, podremos comprobar que el frenado del péndulo ha disminuido significativamente. Esto no quiere decir que las corrientes hayan desaparecido, sino que debido a la limitación de la banda donde actúa, limitado por los cortes realizados, éstas se ven muy mermadas.
Para disminuir el desarrollo de las corrientes de Foucault se emplea el sistema de construir los núcleos de hierro en lugar de macizos, mediante chapas o láminas superpuestas con un espesor de 0.2 a 0.6 mm, aisladas unas de las otras con barniz o papel. Las chapas se hacen con un acero al silicio de alta resistividad, de modo que la intensidad de la corriente inducida disminuye y las pérdidas alcanzan así un valor admisible. Esta construcción no produce la disminución del flujo magnético, pues se dispone siempre según el plano que recorren las líneas de fuerza.
La calidad de estas láminas en cuanto a las pérdidas por histéresis y corrientes de Foucault se caracteriza por la potencia en vatios(W), disipada por kilo de plancha sometido a una inducción alternativa de una tesla, a razón de 50 ciclos de imantación por segundo.
La siguiente tabla da los valores de las pérdidas específicas en W/kg, para diversas calidades de planchas magnéticas que existen en el mercado.
-
-
-
-
Pérdida específica (W/kg) Espesor (mm) Pérdida específica (W/kg) Espesor (mm) 3.0 0.5 1.3 0.35 2.6 0.5 1.1 0.35 2.3 0.5 1.0 0.35 2.0 0.5 0.9 0.35 1.7 0.5 0.5 0.35 1.5 0.5
-
-
-
En los núcleos de hierro utilizados en las bobinas de alta frecuencia, la disposición clásica en láminas, que hemos visto antes, ya no es suficiente, por lo que, estos núcleos están construidos con hierro especial, de polvo comprimido y aglomerado con barniz aislante, de tal manera que cada grano de hierro se encuentra aislado de sus más próximos, siendo ésta la única forma de reducir las pérdidas en el hierro, hasta conseguir un valor aceptable.
| Movimiento de una pieza conductora hacia y desde un campo magnético uniformeModelo simple que calcula la fuerza de frenado. Disco que se mueve en un campo magnético uniforme Corrientes de Foucault en una pieza metálica de forma cilíndrica Referencias | ||||||||||||||||
| Hasta ahora hemos considerado ejemplos en los cuales las corriente inducidas están obligadas a seguir trayectorias bien definidas a través de hilos hechos de material conductor. Los equipos eléctricos están formados por piezas, trozos de conductor que se mueven en un campo magnético o están situadas en un campo magnético variable, dando lugar a corrientes inducidas que circulan por el volumen del conductor. Estas corrientes se denominan de Foucault.
Cuando se coloca una pieza de metal en un campo magnético variable con el tiempo B(t), se genera un campo eléctrico que produce un movimiento de las cargas libres en el conductor metálico, generando corrientes.
Estas corrientes disipan energía en el metal en forma de calor. Daremos un ejemplo, en la siguiente página dedicada a las corrientes de Foucault.
Cuando una pieza de metal se mueve en una región en la que existe un campo magnético no uniforme pero constante en el tiempo B(r) se generan corrientes y la energía se disipa en el conductor metálico. Este fenómeno se puede explicar por medio de la fuerza de Lorentz. A causa de la disipación de la energía se produce una fuerza de frenado que disminuye la velocidad de la pieza metálica.
En esta página, daremos una descripción cualitativa de las corrientes de Foucault, teniendo presente el comportamiento de una espira que atraviesa una región en la que existe un campo magnético uniforme con velocidad constante. A continuación, mediante un modelo simple se demostrará que la fuerza de frenado es proporcional a la velocidad de la pieza metálica, concluyendo con un programa interactivo, que muestra los efectos de la fuerza de frenado en un disco en rotación como el que se muestra en la figura..
Movimiento de una pieza conductora hacia y desde un campo magnético uniformeEl efecto de las corrientes de Foucault es una disipación de la energía por efecto Joule. Estas pérdidas se intentarán reducir al máximo posible en los núcleos de un transformador, pero puede ser interesante aumentarlas para realizar un frenado electromagnético (amortiguamiento, freno eléctrico) o en la producción del calor (horno de inducción).El comportamiento de una pieza metálica rectangular que se mueve hacia o sale de una región donde existe un campo magnético uniforme es esencialmente el mismo que el de una espira que se mueve hacia o sale de una región donde existe un campo magnético uniforme perpendicular a la espira.
Modelo simple que calcula la fuerza de frenado.
Sea una pieza metálica larga y ancha y de pequeño espesor que se mueve con velocidad constante v. Un campo magnético B uniforme perpendicular al plano de la hoja metálica se aplica a una pequeña porción rectangular de dimensiones a y b.
Se supondrá que el campo magnético producido por las corrientes inducidas es suficientemente pequeño, para considerar que la fuerza de frenado proviene únicamente de la acción del campo magnético externo sobre las corrientes inducidas. Esto se produce si la velocidad v de la pieza metálica es inferior a una velocidad característica vc, que depende de la conductividad del metal y del espesor de la pieza.
Supongamos que el campo magnético B es perpendicular al plano de la hoja metálica, al moverse la pieza metálica con velocidad v, los portadores de carga q existentes en la pequeña región rectangular de dimensiones a y b experimentan una fuerza fm=q(v×B), tal como se muestra en la figura. Los portadores de carga son impulsados por la fuerza magnética hacia la derecha.
La separación de cargas produce un campo eléctrico E=-v×B, dirigido hacia la izquierda. Tenemos el equivalente a una batería cuya fem es igual a la diferencia de potencialVε =vBa medida en circuito abierto.
La pequeña región rectangular no está aislada del resto de la hoja metálica, que proporciona la conexión entre los dos terminales de la imaginaria batería por el que circula una corriente de intensidad i. El resto de la pieza metálica opone una resistencia R al paso de la corriente eléctrica. Mientras que la pequeña región rectangular presenta una resistencia interna r que podemos calcular aplicando la ley de Ohm.
siendo δ el espesor de la pieza metálica y σ la conductividad del metal. La ecuación del circuito se escribe i(r+R)=Vε
El cálculo de la resistencia R de la pieza metálica excepto la región rectangular es muy complicado.
La fuerza Fm se opone a la velocidad v de la pieza metálica y es proporcional a su velocidad, y al cuadrado del campo magnético B. El producto δab es el volumen de la porción de la pieza metálica que está bajo la influencia del campo magnético uniforme B.
La energía disipada en la unidad de tiempo, es el producto de la fuerza por la velocidad, Fm·v, es proporcional al cuadrado del producto de la intensidad del campo magnético por la velocidad.
Deducción alternativa
De la ley de Ohm y de la fuerza de Lorentz, calculamos la densidad de corriente J
J=σ(E+v×B)
Si J es uniforme en la sección bδ, la intensidad i de la corriente que fluye por la región rectangular es J=i/(bδ)i
El primer término es la fem inducida Vε=vBa, el término que multiplica la intensidad es la resistencia r que presenta la región rectangular al paso de la corriente.
V es la diferencia de potencial en los terminales de la batería, y es también la diferencia de potencial entre los extremos de la resistencia R, por lo que V=iR. Llegamos a la ecuación del circuito vBa=i(r+R)
El elemento de volumen dV=bδ·dx, señalado en color amarillo en la figura
Obtenemos el mismo resultado
Disco que se mueve en un campo magnético uniformeConsideremos un disco que se mueve en un campo magnético uniforme perpendicular al plano del disco, pero limitado a una porción de su superficie. Tenemos ahora una doble corriente en forma de torbellino, que circula en sentidos contrarios, en el borde anterior y posterior del campo magnético.
Donde k es una constante que depende de la conductividad del material del que está hecho el disco, la intensidad del campo magnético y la posición y tamaño de la porción de la superficie del disco sobre la que actúa el campo magnético. Una situación análoga al movimiento vertical de una varilla en un seno de un campo magnético uniforme. Ecuación de la dinámica de rotaciónSupongamos un disco de momento de inercia I0 que se le proporciona una velocidad angular w0 en el instante inicial. La velocidad angular del disco en el instante t se obtiene a partir de la ecuación de la dinámica de rotaciónLa velocidad angular disminuye exponencialmente con el tiempo. El péndulo de Pohl es un disco que puede oscilar angularmente gracias al momento que ejerce sobre el mismo un muelle helicoidal. Un dispositivo de este tipo describe oscilaciones libres. Si al disco se le acopla un anillo de metal (normalmente cobre) y se le hace girar entre los polos un electroimán tenemos un modelo de oscilador amortiguado. Dependiendo de la intensidad de la corriente en el electroimán, el campo puede ser mayor o menor. El momento de la fuerza de frenado magnético puede hacerse suficientemente grande de modo que el sistema deje de oscilar, estamos en el caso de las oscilaciones críticas y sobreamortiguadas. ActividadesSe introduce
Se observa el movimiento de rotación del disco, como va disminuyendo su velocidad angular. Las corriente inducidas se visualizan mediante el movimiento de puntos de color rojo que representan a portadores de carga positivos. Las corrientes inducidas se originan en la región en la que existe campo magnético y se cierran por fuera de dicha región tal como vimos en el movimiento de una espira en el seno de un campo magnético uniforme. Si activamos la casilla titulada Fuerza sobre las cargas, se representan los vectores
|
Corrientes de Foucault en una pieza metálica de forma cilíndricaYa hemos estudiado el problema de la corriente inducida que se genera cuando una espira está en una región en la que el campo magnético varía con el tiempo.
F =Bx·p r2 La fem inducida en la línea de corriente de radio r es Esta fem es la que pone en movimiento a los portadores de carga contenidos el volumen de la capa cilíndrica de longitud L comprendida entre r y r+dr. Originando una intensidad i=Vε/ReSiendo Re la resistencia del tubo (no confundirla con el radio R del cilindro) de longitud 2p r y de sección Ldr por el que circulan las cargas. La fórmula de la resistencia (resistividad por longitud del conductor y dividido por su sección) se expresa donde r es la resistividad del material. Por tanto, la intensidad es La energía por unidad de tiempo (potencia) disipada es Vε·di, y para calcular la potencia total se integra entre 0 y R (radio del cilindro) Teniendo en cuenta que el valor medio durante un periodo 2p /w de la función periódica coseno cuadrado es1/2. La potencia disipada es proporcional al cuadrado de la frecuencia ω del campo magnético variable. Esta es la razón por la que los hornos de inducción utilizan frecuencias elevadas. En esta deducción se ha despreciando el campo magnético creado por las propias corrientes de Foucault. Esta aproximación no es válida para materiales de resistividad nula (materiales superconductores). En los transformadores no podemos cambiar la frecuencia, ni la resistividad del material empleado como núcleo (se emplea un determinado tipo de material). Para reducir la pérdidas se actúa sobre la geometría de las líneas de corriente, se tratará de reducir sus dimensiones (fijarse que la potencia disipada <P> es proporcional a la cuarta potencia del radio del cilindro).
|








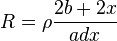
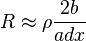
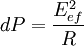
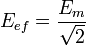


![dP={1 \over \rho}B^2_m.w^2 b.a\left [ \frac{x^3}{3} \right ]^{e\over 2}](https://upload.wikimedia.org/math/f/e/1/fe17e1e654c336099f91e835174fc2fb.png)

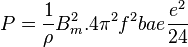

No hay comentarios:
Publicar un comentario