La función escalón unitario
Observaciones:
- t-t0 recibe el nombre de ARGUMENTO,
- to se llama DISCONTINUIDAD.
- Normalmente t0= 0.
- Cuando t0 es diferente de cero, se dice que la función está DESFASADA, o que el argumento está desfasado.
- En circuitos se lleva a cabo una CONMUTACIÓN en t=0 o en t=t0.
- La funcion escalón unitario es solo un modelo matemático de una operación real de conmutación.
- Aunque la subida o bajada no es estrictamente parte de la definición del escalón unitario, generalmente se incluye en todas las gráficas.
- u(t) es ADIMENSIONAL. Si queremos que u(t) represente un voltaje o una corriente es necesario multiplicar a u(t) por algún voltaje o corriente, así:
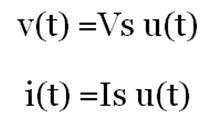
- La funcion escalón unitario no tiene que ser necesariamente una función del tiempo.
Funciones singulares
Son funciones que son discontinuas o que tienen derivadas discontinuas.
La función escalón unitario y la función impulso unitario son funciones discontinuas y pueden ser una función de la frecuencia, como se verá mucho más adelante en este curso.
Posibilidades de la función escalón unitario
Los números identificadores a la izquierda de las siguientes funciones indican el cuadrante donde alcanzan el valor 0, 1 ó -1. Los dos primeros números están a la izquierda del eje vertical.
Un cambio instantáneo en otro momento que no sea t=0 puede representarse por medio de una función escalón que tiene:
- Un argumento desfasado
- Una inversión de signo
- Ambas cosas: un argumento desfasado y un cambio de signo
Sumas de funciones escalón
Funciones equivalentes
Son aquellas cuyas características de voltaje-corriente son idénticas.
Analizaremos qué fuentes físicas son equivalentes a las fuentes de voltaje y corriente escalón.
Fuente ideal de voltaje escalón
La corriente puede tomar cualquier valor en cualquiera de los dos intervalos, tt0.
Fuente real de voltaje escalón
El EQUIVALENTE FÍSICO aproximado de una función de excitación escalón es un interruptor o suiche en serie con una batería.
La función de excitación o fuente vale cero hasta que se cierra el suiche, y después es igual al voltaje Vs de la batería. La fuente tiene una discontinuidad en el instante en que se cierra el interruptor en t=t0.
La aplicación SÚBITA de una fuente es su aplicación en el tiempo cero o en t0.
Equivalente 1
No es equivalente para t
Además, antes del cierre v (t) tiene un valor determinado por los elementos activos de la red general. Aún si la red general es pasiva existen cargas estáticas que pueden resultar en un valor diferente de cero para v (t).
Este modelo solo es equivalente para t>t0 si las corrientes que fluyen de las dos redes son idénticas en t=t0.
Ningún arreglo de funciones de excitación escalón de voltaje pueden dar el equivalente exacto si no se conoce el voltaje en t
Equivalente 2
Este equivalente asegura que v(t) es cero en tt0.
Pero no es equivalente en t=to ya que la fuente Vs está momentáneamente en corto, es decir, Vs =0. En el modelo real la fuente Vs debería poder soportar la corriente de cortocircuito.
Fuente ideal de corriente escalón
Fuente real de corriente escalón
Equivalente
No es equivalente en t
Función resistencia escalón
Un interruptor es una resistencia que cambia instantáneamente de infinito a cero ohmios y viceversa. Sin embargo, no puede llevarse a cabo una operación de conmutación en un tiempo cero. Es decir, un interruptor es una resistencia dependiente del tiempo, y recibe el nombre de función escalón resistencia.
Un interruptor normalmente abierto (N.A.) es una resistencia que cambia instantáneamente desde infinito hasta cero ohmios.

Un interruptor normalmente cerrado (N.C.) es una resistencia que cambia instantáneamente desde cero ohmios hasta infinito.
En muchos circuitos los tiempos de conmutación son menores a 1 nanosegundo, que es mucho menor que las constantes de tiempo del circuito. Hablaremos de constantes de tiempo más adelante, cuando veamos circuitos RL y RC.
Una conmutación presenta problemas como:
- Arqueo
- Resistencia
- Rebote de contactos
- Capacitancia de contactos.
Pulso rectangular de voltaje
Fuente pulso senoidal
Ejemplo 1 Funciones Escalón
Evalúe la siguiente función en t= 1,5 segundos
Solución
Como t=1,5
Sumando,
Ejemplo 2 Funciones Escalón
Evalúe la siguiente función en t= 1,5 segundos
Solución
Como t=1,5
Ejemplo 3 Funciones Escalón
Evalúe la siguiente función en t= 1,5 segundos
Solución
Como t=1,5
Ejemplo 4 Funciones Escalón
Calcular V3 en t=1 segundo
Ejemplo 5 Funciones Escalón
Calcular V3 en t=3 segundos
Ejemplo 6 Funciones Escalón
Calcular V3 en t=5 segundos
analisisdecircuitos1.wordpress.com


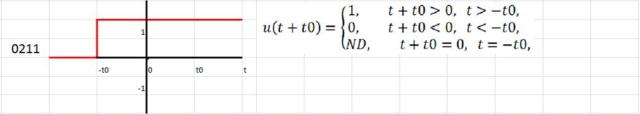
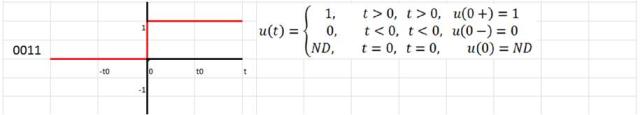

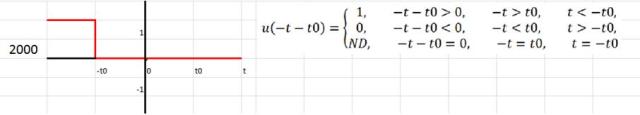
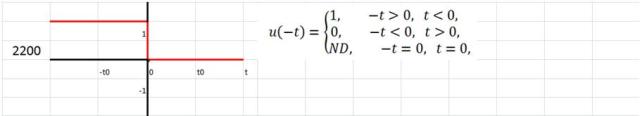

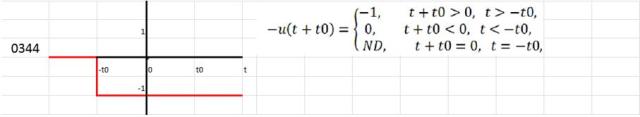
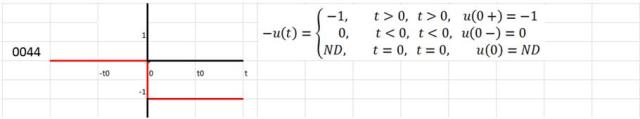
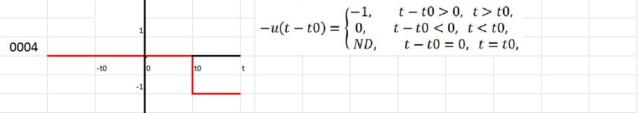
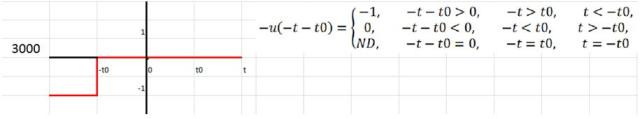
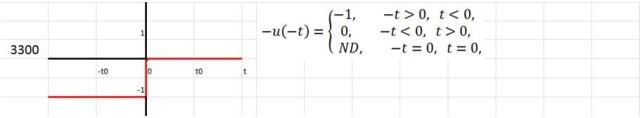
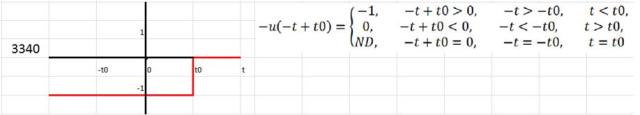


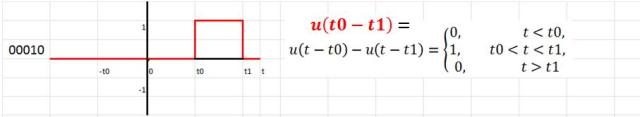

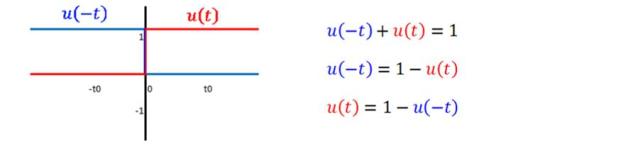
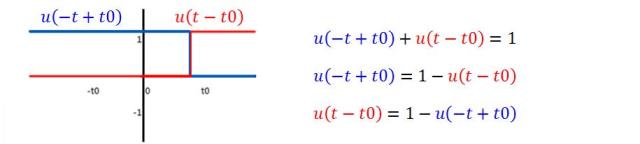

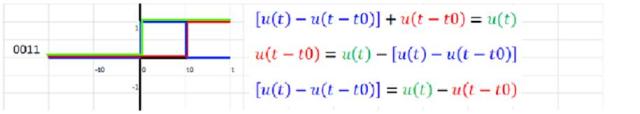
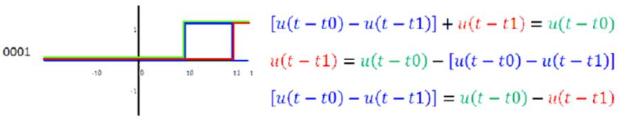










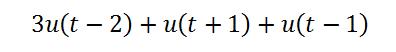




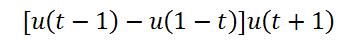



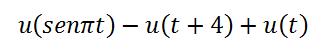













No hay comentarios:
Publicar un comentario