Cálculo diferencial
función diferenciable es una generalización para el cálculo en varias variables del concepto más simple de función derivable. En esencia una función diferenciable admite derivadas en cualquier dirección y puede aproximarse al menos hasta primer orden por una aplicación afín.
La formulación rigurosa de esta idea intuitiva sin embargo es algo más complicada y requiere de conocimientos de álgebra lineal. Debe notarse que aunque una función de varias variables admita derivadas parciales según cada una de sus variables no necesariamente eso implica que sea una función diferenciable.
Definición
Una función de múltiples variables  se dirá diferenciable en
se dirá diferenciable en  si, siendo
si, siendo  un conjunto abierto en
un conjunto abierto en 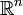 , existe una transformación lineal
, existe una transformación lineal 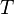 que cumpla:
que cumpla:
 se dirá diferenciable en
se dirá diferenciable en  si, siendo
si, siendo  un conjunto abierto en
un conjunto abierto en 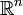 , existe una transformación lineal
, existe una transformación lineal 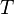 que cumpla:
que cumpla:
Donde  cumple que:
cumple que:
 cumple que:
cumple que:
o sea  tiende a cero "más rápido" que función lineal, cuando h tiende a 0. Necesariamente la transformación lineal
tiende a cero "más rápido" que función lineal, cuando h tiende a 0. Necesariamente la transformación lineal  es la única cosa que se ve más claramente si adoptamos como definición de función derivable aquella para la cual se cumple que exista una aplicación lineal tal que:
es la única cosa que se ve más claramente si adoptamos como definición de función derivable aquella para la cual se cumple que exista una aplicación lineal tal que:
 tiende a cero "más rápido" que función lineal, cuando h tiende a 0. Necesariamente la transformación lineal
tiende a cero "más rápido" que función lineal, cuando h tiende a 0. Necesariamente la transformación lineal  es la única cosa que se ve más claramente si adoptamos como definición de función derivable aquella para la cual se cumple que exista una aplicación lineal tal que:
es la única cosa que se ve más claramente si adoptamos como definición de función derivable aquella para la cual se cumple que exista una aplicación lineal tal que:Visualización Geométrica
Para fijar ideas, usando una función  cuyo gráfico sería una "sábana". La función es diferenciable si la "sábana" no está "quebrada" en los puntos donde es diferenciable, o sea la función es "suave" en todos los puntos de su dominio, existiendo la matriz jacobiana o derivada en esos puntos.
cuyo gráfico sería una "sábana". La función es diferenciable si la "sábana" no está "quebrada" en los puntos donde es diferenciable, o sea la función es "suave" en todos los puntos de su dominio, existiendo la matriz jacobiana o derivada en esos puntos.
 cuyo gráfico sería una "sábana". La función es diferenciable si la "sábana" no está "quebrada" en los puntos donde es diferenciable, o sea la función es "suave" en todos los puntos de su dominio, existiendo la matriz jacobiana o derivada en esos puntos.
cuyo gráfico sería una "sábana". La función es diferenciable si la "sábana" no está "quebrada" en los puntos donde es diferenciable, o sea la función es "suave" en todos los puntos de su dominio, existiendo la matriz jacobiana o derivada en esos puntos.Funciones reales de una variable
Una función real de una variable que admite derivada en todos sus puntos y tal que dicha derivada sea continua es trivialmente una función diferenciable. Por esa razón para funciones reales de una variable el concepto de función derivable y función diferenciable son básicamente equivalentes.
Sin embargo, para funciones de más de una variable la situación es más complicada. Ya que la existencia de derivadas no comporta que una función sea automáticamente diferenciable.
Ejemplos para funciones de dos variables
De función diferenciable
La función f(x,y) es diferenciable si x, y son diferentes de 0, puesto que existen las derivadas parciales en un entorno de cualquier punto y son continuas en él:
De función derivable no-diferenciable
En cambio la función g(x,y) es continua, admite derivadas según las variables x e y, e incluso derivadas direccionales, sin embargo no es diferenciable en (0,0):
De función no-continua y no-diferenciable
La función  no es diferenciable en (0,0) puesto que no es continua en ese punto ni existen derivadas parciales de cualquier orden en el punto (0,0):
no es diferenciable en (0,0) puesto que no es continua en ese punto ni existen derivadas parciales de cualquier orden en el punto (0,0):
 no es diferenciable en (0,0) puesto que no es continua en ese punto ni existen derivadas parciales de cualquier orden en el punto (0,0):
no es diferenciable en (0,0) puesto que no es continua en ese punto ni existen derivadas parciales de cualquier orden en el punto (0,0):Función diferenciable de varias variables
Una aplicación vectorial entre varias variables de la forma  se dice diferenciable en un punto
se dice diferenciable en un punto  si puede encontrarse una matriz
si puede encontrarse una matriz 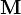 , llamada matriz jacobiana, que representa una aplicación lineal
, llamada matriz jacobiana, que representa una aplicación lineal  tal que:
tal que:
 se dice diferenciable en un punto
se dice diferenciable en un punto  si puede encontrarse una matriz
si puede encontrarse una matriz 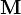 , llamada matriz jacobiana, que representa una aplicación lineal
, llamada matriz jacobiana, que representa una aplicación lineal  tal que:
tal que:
O de forma equivalente:
donde  es un punto de
es un punto de 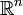 ,es decir
,es decir  y
y 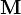 , la transformación lineal, que viene dada por la matriz jacobianade
, la transformación lineal, que viene dada por la matriz jacobianade  en el punto
en el punto 
 es un punto de
es un punto de 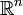 ,es decir
,es decir  y
y 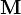 , la transformación lineal, que viene dada por la matriz jacobianade
, la transformación lineal, que viene dada por la matriz jacobianade  en el punto
en el punto 
En esas condiciones se puede ver la función  admite derivadas parciales de todas las variables y además resulta:
admite derivadas parciales de todas las variables y además resulta:
 admite derivadas parciales de todas las variables y además resulta:
admite derivadas parciales de todas las variables y además resulta:Diferenciabilidad de funciones vectoriales
Los conceptos de derivable y diferenciable coinciden en funciones vectoriales. Basicamente lo que hacemos aquí es derivar componente a componente.SeaPor ejemplo si
La diferencial de
Diferenciabilidad de campos escalares
Un campo escalaren este caso la aplicación lineal
Así pues si
donde
Propiedades de la diferencial
- Si un campo escalar
es diferenciable en
, entonces
es continuo en
. Por tanto si no es continuo no puede ser diferenciable.
- Si
es constante, entonces para cada
,
es la aplicación lineal nula.
- Si
es lineal, entonces para cada
,
.
. En términos matriciales esta propiedad es
.
Derivadas parciales
Sea- Cuando el vector es unitario,
, se habla de derivada direccional según el vector
.
- Cuando
es el
-ésimo vector de la base canónica, se habla de derivada parcial
-ésima. En este caso se usan también otras notaciones









No hay comentarios:
Publicar un comentario