Función implícita
Una función y(x) se llama implícita cuando está definida de la forma F(x, y) = 0 en lugar de la habitual.
Por ejemplo, puede probarse que la siguiente ecuación define una función implícita en cierta región de  entre las variables x e y:
entre las variables x e y:
 entre las variables x e y:
entre las variables x e y:
Diferenciación
Para poder derivar una función implícita se usa la regla de la cadena, en el caso de la variable independiente no hay problema ya que se deriva directamente, para la variable dependiente se considera como una función que a su vez está en función de la variable independiente:Dada una función , implícita, si queremos calcular la derivada de y respecto de x:
, implícita, si queremos calcular la derivada de y respecto de x:  .Si consideramos
.Si consideramos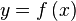 es una función en términos de la variable independiente x y
es una función en términos de la variable independiente x y  es una función en términos de la variable dependiente y, dado que
es una función en términos de la variable dependiente y, dado que 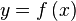 , entonces para obtener la derivada:
, entonces para obtener la derivada:Ejemplo
Obtener la derivada de:El término se puede considerar que son dos funciones,
se puede considerar que son dos funciones,  y
y  por lo que se derivará como un producto:El término
por lo que se derivará como un producto:El término se deriva como:El término
se deriva como:El término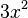 se deriva de forma normal como:El valor constante 12, que no depende ni de x ni de y, tiene por derivada 0, como corresponde a un valor constante.El término
se deriva de forma normal como:El valor constante 12, que no depende ni de x ni de y, tiene por derivada 0, como corresponde a un valor constante.El término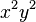 se puede considerar como un producto y se deriva como:Al unir todos los términos se obtiene:Ordenando:Factorizando respecto a (
se puede considerar como un producto y se deriva como:Al unir todos los términos se obtiene:Ordenando:Factorizando respecto a (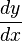 ) los valores son:Finalmente despejando
) los valores son:Finalmente despejando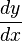 se obtiene la derivada de la función implícita:
se obtiene la derivada de la función implícita: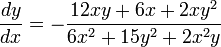
- Derivada de funciones implícitas. La derivada de la función implícita
definida mediante la ecuación
puede calcularse: o bien despejando la y , o bien, mediante la siguiente fórmula:
, siempre que
Las derivadas de orden superior de una función implícita se pueden calcular mediante la derivación sucesiva de la fórmula anterior, considerando y como función de x.Las derivadas parciales de una función implícita de dos variablesdefinida mediante la ecuación
puede calcularse mediante las fórmulas:
;
, siempre que
Dada la ecuaciónSi el punto
cumple la ecuación
, la función F tiene derivadas parciales continuas en un entorno de
y
entonces la ecuación
define una función explícita
en un entorno de
con
Dada la ecuaciónSi el punto
cumple la ecuación
, la función F tiene derivadas parciales continuas en un entorno de
y
entonces la ecuación
define una función explícita
en un entorno de dicho punto.
Volver al comienzo de la Página
—————————————————————————————————22. Calcula y', siendo
Solución:Tenemos:hallamos las derivadas parciales:;
Por lo tanto:Volver al comienzo de la Página
—————————————————————————————————23. Calculay
, siendo
Solución:Tenemos:hallamos las derivadas parciales:;
;
Por lo tanto::
Volver al comienzo de la Página
—————————————————————————————————24. Demuestra que la ecuacióndefine en un entorno del punto (1, 1) una función
Calcula y'(1) e y''(1)
Solución:a) Existencia de la función explícita:Consideramos la función:tenemos:
F es diferenciable con continuidad eny por lo tanto en un entorno de (1, 1)
Luego, de acuerdo con el teorema de existencia de funciones implícitas existeen un entorno de 1 con
b) Cálculo de y'(1)Derivamos la ecuaciónteniendo en cuenta que y es función de x
sustituyendo
c) Cálculo de y''(1)Derivando la ecuaciónse tiene.
Este caso particular también se podía haber resuelto despejandoy eligiendo el signo + ya que
Volver al comienzo de la Página
—————————————————————————————————25. Calcula dz en la ecuación
Solución:Consideramos la función:Hallamos las derivadas parcialesCon lo cualCon lo que resulta: - La fórmula de Faà di Bruno es una identidad que generaliza la regla de la cadena a derivadas de orden superior, llamada así en honor al matemático italiano Francesco Faà di Bruno (1825-1888) , aunque él no fue el primero en afirmar o demostrar la fórmula. En 1800, más de 50 años antes de Faà di Bruno, el matemático francés Louis François Antoine Arbogast (1759-1803) declaró la fórmula en un libro de cálculo,1 considerada la primera referencia publicada al respecto sobre el tema.2Quizás, la forma más conocida de la fórmula Faa di Bruno dice que:
 ,donde la suma es sobre todas las n-tuplas de enteros no negativos (m1, …, mn) que satisfacen la restricción:
,donde la suma es sobre todas las n-tuplas de enteros no negativos (m1, …, mn) que satisfacen la restricción: .A veces, para darle un patrón memorable, esta está escrita en una forma en la que los coeficientes que tienen la interpretación combinatoria que se discuten a continuación son menos explícitos:
.A veces, para darle un patrón memorable, esta está escrita en una forma en la que los coeficientes que tienen la interpretación combinatoria que se discuten a continuación son menos explícitos: .Combinando los términos con el mismo valor de m1 + m2 + ... + mn = k y notando que m j tiene que ser cero para j > n − k + 1 proporciona una fórmula algo más sencilla en términos de polinomios de Bell Bn,k(x1,...,xn−k+1):
.Combinando los términos con el mismo valor de m1 + m2 + ... + mn = k y notando que m j tiene que ser cero para j > n − k + 1 proporciona una fórmula algo más sencilla en términos de polinomios de Bell Bn,k(x1,...,xn−k+1): .La fórmula de Faà di Bruno da una ecuación explícita para la
.La fórmula de Faà di Bruno da una ecuación explícita para laTH derivado de la composición
.Si
y
son funciones para las que se definen todos los derivados necesarios, a continuación,
(1)(2)(Roman 1980).(3)(M. Alekseyev, com. Pers., Nov. 3, 2006).La fórmula de Faà di Bruno se puede convertir en un marco que es un caso especial de un álgebra de Hopf (Figueroa y Gracia-Bondía 2005).Las primeras derivados para simbólicay
están dadas por
(4)(5)

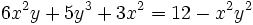
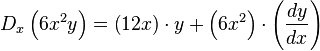




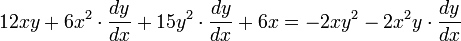
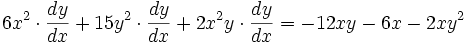

No hay comentarios:
Publicar un comentario