Algoritmo de avance-retroceso
Introducción
Uno de los problemas básicos de los Modelos Ocultos de Márkov es el cálculo de la probabilidad de una secuencia de observables dado un modelo . El objetivo es por tanto calcular eficientemente .
Probabilidad de una secuencia de estados
Supongamos una secuencia de estados . La probabildad de esta secuencia es:
Probabilidad de una secuencia de observables dada una secuencia de estados
La probabilidad de observar cuando se da precisamente esta secuencia de estados es:
Cada corresponde con el valor de
Probabilidad de una secuencia de observables dado un modelo
Por tanto, para obtener la probabilidad de una secuencia de observables dado un modelo , deberíamos calcular la probabilidad de para cada una de las secuencias posibles .
El cálculo de tal y como se muestra es impracticable; sólo para estados y observaciones sería necesario realizar del orden de operaciones. Para reducir esta complejidad se emplean estrategias de programación dinámica como los algoritmos forward y backward.
Se recomienda revisar la formalización habitual de un Modelo Oculto de Márkov para comprender cada uno de los elementos en la formulación de estos dos procedimientos.
Procedimiento hacia adelante
Cálculo de
Consideramos la variable como:
Dado el modelo , es la probabilidad de observar y estar en el instante de tiempo en el estado .
Cálculo hacia adelante de la probabilidad de una secuencia de observaciones.
Inicialización
Recurrencia
,
Terminación
Ejemplo de cálculo de
El esquema muestra los estados y probabilidades necesarias para el cálculo de :
Cálculo hacia atrás
Cálculo de
Consideramos la variable .
Dado el modelo , es la probabilidad de la secuencia de observación desde el instante de tiempo hasta el final, cuando el estado en el instante de tiempo es.
Inicialización
,
Recurrencia
,
,
Terminación
Ejemplo de cálculo de
El esquema muestra los estados y probabilidades necesarios para el cálculo de para un modelo de 5 estados y una secuencia de observaciones de longitud 5.
Complejidad computacional
Tanto el procedimiento hacia adelante como el algoritmo backward, requieren del orden de operaciones; muy inferior a operaciones ( es el número de estados y es la longitud de la secuencia de observaciones) que son necesarias si se calcula para todas las posibles secuencias del modelo.
El cálculo de los servirán - junto a los - para contestar las otras dos preguntas fundamentales de los Modelos Ocultos de Márkov:
- ¿Cuál es la secuencia óptima de estados dado una secuencia de observaciones ? (algoritmo de Viterbi)
- Dada una secuencia de observaciones , ¿cómo podemos estimar los parámetros del modelo para maximizar . En este caso el objetivo es encontrar el modelo que mejor explica la secuencia observada (algoritmo de Baum-Welch).
Algoritmo de Baum-Welch
Introducción
Uno de los problemas relacionados con los Modelos Ocultos de Márkov (MOM) es el de encontrar un modelo que maximice la probabilidad de una secuencia de observaciones , es decir, determinar el modelo que mejor explica tal secuencia. El problema es que no es posible encontrar tal modelo analíticamente y por ello es necesario un algoritmo iterativo como el de Baum y Welch, que permite estimar los parámetros de un modelo que hacen máxima la probabilidad de una secuencia de observables.
El algoritmo de Baum y Welch
Dada una secuencia de observaciones , el algoritmo de Baum y Welch permite estimar los parámetros de un Modelo oculto de Márkov (MOM) que maximizan la probabilidad de dicha secuencia, es decir, .
Valores esperados
Antes de describir el proceso de estimación, necesitamos conocer:
- el número esperado de transiciones desde el estado en y
- el número esperado de transiciones desde el estado al estado en
Para ello definimos previamente como la probabilidad de estar en el estado en el instante y en el estado en el instante , dado una observación y el modelo .
donde los valores y se pueden calcular eficientemente con el algoritmo de avance-retroceso.
La figura muestra un esquema parcial de los elementos necesarios para el cálculo de .
Definimos también como la probabilidad de estar en el estado en el instante ,
Sumando cada en cada instante de tiempo, obtenemos:
- el número esperado de transiciones desde el estado en la observación
y haciendo lo mismo con cada , obtenemos:
- el número esperado de transiciones desde el estado al estado en la observación
Reestimación
El funcionamiento del procedimiento iterativo es básicamente el siguiente:
- Se parte de un modelo inicial que se puede seleccionar aleatoriamente.
- Se realiza el cálculo de las transiciones y símbolos de emisión que son más probables según el modelo inicial escogido.
- Se construye un nuevo modelo en el que se incrementa la probabilidad de las transiciones y símbolos determinados en el paso anterior. Para la secuencia de observables en cuestión, el modelo tendrá ahora una probabilidad mayor que el modelo anterior.
Este proceso de entrenamiento se repite varias veces hasta que no exista mejora entre un modelo y el siguiente revisado.
Probabilidad de estar en el estado en el instante de tiempo :
Reestimación de las probabilidades de transición. El numerador representa el número esperado de transiciones de a , y el denominador representa el número esperado de transiciones desde :
,
Reestimación de las probabilidades de emisión. El numerador representa el número esperado de veces que se pasa por el estado y se observa , y el denominador representa el número esperado de veces que se pasa por el estado :
,
Otras preguntas fundamentales
Otros dos problemas que es importante saber resolver para utilizar los MOM son:
- ¿Cuál es la secuencia óptima de estados, dada una secuencia de observaciones ? (algoritmo de Viterbi)
- ¿Cuál es la probabilidad de una secuencia de observaciones dado un modelo ? Es decir, ¿cómo podemos calcular de forma eficiente ? (cálculo hacia adelante y hacia atrás).
El algoritmo de Baum-Welch y el Modelo oculto de Markov
Leonard Baum y Welch Lloyd diseñaron un algoritmo de modelado probabilístico para detectar patrones en elmodelo oculto de Markov. Se basan en la teoría de funciones de probabilidad de una Cadena de Markov y elalgoritmo esperanza-maximización (algortimo EM) – un método iterativo para encontrar la máxima verosimilitud de los parámetros en los modelos estadísticos, en los que el modelo depende de variables latentes no observables.

Fuente Data Science Central
El algoritmo de Baum-Welch demostró inicialmente ser una herramienta de notable reconocimiento a la hora de descifrar códigos y el lenguaje, pero también tiene aplicaciones para negocios, finanzas, ciencias y otros. El algoritmo encuentra parámetros desconocidos de un modelo oculto de Markov.
El algoritmo consta de dos fases:
1 . Calcular las probabilidades a posteriori para un determinado modelo , y
2 . volver a estimar los parámetros del modelo .
2 . volver a estimar los parámetros del modelo .
El modelo de un proceso de Markov es una secuencia de eventos que no tienen una relación directa. Un modelo oculto de Markov es un modelo probabilístico de una colección de variables aleatorias y el cual proporciona un marco sencillo y eficaz para el modelado de las secuencias del vector espectral para variables del tiempo .
El algoritmo de Baum- Welch y el modelo oculto de Markov se utilizan con éxito para los sistemas de comercio financiero, predicción de las tendencias del mercado, la detección de fraudes, optimización de cadenas, previsión de la oferta y la demanda, predicción de series de tiempo financieras y la detección de anomalías en la actividad de tráfico de red.
Con suficientes datos y potencia de computación, los modelos de algoritmo de Baum- Welch y el modelo oculto de Markov pueden calcular las probabilidades de que un proceso ocurra y predecir eventos futuros.
 dado un modelo
dado un modelo  . El objetivo es por tanto calcular eficientemente
. El objetivo es por tanto calcular eficientemente  .
. de estados
de estados . La probabildad de esta secuencia es:
. La probabildad de esta secuencia es:
 dada una secuencia de estados
dada una secuencia de estados  cuando se da precisamente esta secuencia de estados
cuando se da precisamente esta secuencia de estados 
 corresponde con el valor de
corresponde con el valor de 


 estados y
estados y  operaciones. Para reducir esta
operaciones. Para reducir esta 

 y estar en el instante de tiempo
y estar en el instante de tiempo  en el estado
en el estado  .
.

![{\displaystyle \alpha _{t+1}(j)={\biggl [}\displaystyle \sum _{i=1}^{N}{\alpha _{t}(i)a_{ij}}{\biggr ]}b_{j}(o_{t+1})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3226e1dc082e9c82be9f84a2e92b2f2ef5e8751a)
 ,
, 


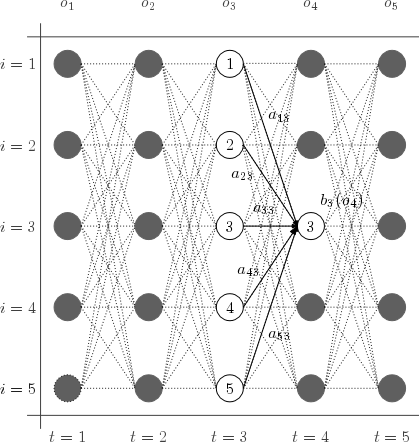
![{\displaystyle \alpha _{4}(3)={\biggl [}\displaystyle \sum _{i=1}^{5}{\alpha _{3}(i)a_{i3}}{\biggr ]}b_{3}(o_{4})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71b549caf1e5df14e80d713015e781ee2841ff92)


 hasta el final, cuando el estado en el instante de tiempo
hasta el final, cuando el estado en el instante de tiempo  ,
, ,
, ,
, 



 operaciones; muy inferior a
operaciones; muy inferior a  operaciones (
operaciones ( es el número de estados y
es el número de estados y  es la longitud de la secuencia de observaciones) que son necesarias si se calcula
es la longitud de la secuencia de observaciones) que son necesarias si se calcula  para todas las posibles secuencias
para todas las posibles secuencias  en
en  como la probabilidad de estar en el estado
como la probabilidad de estar en el estado 



 .
.
 como la probabilidad de estar en el estado
como la probabilidad de estar en el estado 

 , obtenemos:
, obtenemos:
 :
:

 , y el denominador representa el número esperado de veces que se pasa por el estado
, y el denominador representa el número esperado de veces que se pasa por el estado 

No hay comentarios:
Publicar un comentario