CONCEPTOS FÍSICOS

CONCEPTOS FUNDAMENTALES

energía de unión (también llamada energía de separación) es la energía mínima requerida para desmontar un sistema de partículas en partes separadas. Esta energía es igual al defecto de masa: la cantidad de energía, o masa, que se libera cuando se crea un sistema vinculado (que normalmente tiene una energía potencial menor que la suma de sus partes constituyentes), y es lo que mantiene unido al sistema . Si la energía suministrada es más que la energía de enlace, entonces los constituyentes desmontados poseen energía cinética no nula.

Idea general[editar]

En general, la energía de enlace representa el trabajo mecánico que debe realizarse contra las fuerzas que mantienen unido un objeto, desensamblando el objeto en sus partes componentes con una distancia suficiente entre ellas, de modo que una mayor separación requiere un trabajo adicional insignificante.

En los sistemas ligados, si la energía de enlace se elimina del sistema, debe restarse de la masa del sistema independiente, porque esta energía tiene masa. Por lo tanto, si la energía es eliminada (o emitida) del sistema en el momento en que está limitada, esta pérdida de energía también dará como resultado la pérdida de la masa de la energía. ¹​ La masa del sistema no se conserva en este proceso porque el sistema está "abierto" (es decir, no es un sistema aislado de entrada o pérdida de masa o energía) durante el proceso de enlace.

Hay varios tipos de energía de enlace, cada uno operando en una distancia y escala de energía diferentes. Cuanto menor es el tamaño de un sistema encuadernado, mayor es su energía de enlace asociada.

energía negativa es un concepto que se utiliza en física para explicar la naturaleza de ciertos campos, incluyendo el campo gravitatorio y un número de efectos en el campo cuántico.

En algunas teorías hipotéticas, la energía negativa está involucrada en los agujeros de gusano, los cuales permiten el viaje en el tiempo y el impulso de deformación para curvar o distorsionar el espacio tiempo, permitiendo un viaje en el espacio más rápido que la luz.

Energía gravitatoria[editar]

Artículo principal: Energía gravitatoria

La fuerza de atracción gravitatoria entre dos objetos representa la magnitud de energía gravitatoria que atrae a los objetos entre ellos. Cuando están indefinidamente lejos, la atracción gravitatoria que los atrae se acerca a cero. Mientras dos objetos se muevan hacia sí mismos, el movimiento se acelera bajo la acción de la gravedadcausando un aumento en la energía positiva cinética de un sistema. Al mismo tiempo, la atracción gravitatoria - y por tanto energía - también aumenta su amplitud. Pero la ley de la conservación de energía requiere que la energía neta del sistema no cambie. Esto solo puede resolverse si el cambio en energía gravitatoria es negativo, anulando el cambio positivo en la energía cinética. Debido a que la energía gravitatoria se hace más fuerte, la disminución solo puede significar que es negativa.¹​

Un universo en el que la energía positiva dominara, colapsaría eventualmente en un Big Crunch (gran aplastamiento), mientras que en un universo donde la energía negativa dominara se expandiría indefinidamente y eventualmente se desintegraría en un Big Rip (gran desgarro). En el modelo del universo de energía cero, el total de energía en el universo es exactamente cero: la cantidad de energía positiva en forma de materia es cancelada totalmente por su energía negativa en forma de gravedad.²​ Las observaciones actuales apoyan el escenario en el cual el universo se expandirá a un ritmo mayor y, por lo tanto está dominado por la energía negativa. Sin embargo, la naturaleza gravitatoria de esta energía es menos soportada y comúnmente atribuida al misterio de la "energía oscura".³​

Efectos en el campo cuántico[editar]

Las energías negativas y la densidad de la energía negativa son consistentes con la teoría cuántica de campos.⁴​

Efecto Casimir[editar]

Artículo principal: Efecto Casimir

En el efecto Casimir, dos placas planas puestas a una distancia muy corta restringen la longitud de las ondas cuánticas que puedan existir entre ellas. En respuesta, esto restringe los tipos y por ende el número y la densidad de los pares de la partícula virtual que pueden formar en la interferencia en el vacío y puede resultar en una densidad de energía negativa. Esto causa una fuerza atractiva entre las placas, que ya ha sido medida.⁵​

Soluciones negativas de Dirac[editar]

Cuando Paul Dirac formuló en 1928 una ecuación cuántica relativista para describir adecuadamente a los electrones, encontró que junto con soluciones ordinarias que describían electrones (de un modo similar a la ecuación de Schrödinger) aparecían soluciones válidas de dicha ecuación que tenían energía negativa y que no parecían tener una contrapartida en la mecánica cuántica anterior. Con el tiempo, estas soluciones fueron interpretadas como las antipartículas de los electrones, es decir, como positrones.

La existencia de estas soluciones implicaba algunas dificultades teóricas, como que la energía de un sistema de electrones podía no estar acotada inferiormente, y las dificultades que eso ocasiona a la hora de definir un estado fundamental para los electrones de cualquier átomo. Originalmente, Dirac recurrió a la interpretación llamada "teoría de huecos" para resolver esta dificultad. Esta interpretación no resolvía otros problemas como una energía del vacío infinita. Con el tiempo apareció una interpretación diferente que consideraba estas soluciones como antipartículas, asunto que resolvía el problema de la energía infinita del vacío.

Luz Comprimida[editar]

Artículo principal: Luz comprimida

Es posible ordenar múltiples haces de luz láser, tantas que la interferencia cuántica destructiva suprimiera las fluctuaciones del vacío. Tal estado de vacío comprimido involucra a la energía negativa. La forma repetitiva de onda de luz nos lleva a una región alternativa de energía positiva y negativa.⁵​

Radiación de Hawking[editar]

Artículo principal: Radiación de Hawking

Las partículas virtuales con energía negativa pueden existir por un periodo corto de tiempo. Este fenómeno es parte del mecanismo involucrado en la radiación de Hawking, que explica por qué los agujeros negros se evaporan.⁶​

Otras sugerencias[editar]

Física fractal[editar]

La teoría de la física fractal está basada en la idea de escala invariable, que nos dice que un fenómeno puede ser funtamentalmente el mismo, así sea visto desde una escala cósmica o una subatómica. Específicamente, se extiende a las dos Relatividades Especiales postuladas a escala. La primera postulación, asume que la escala uniforme absoluta no puede ser detectada, la segunda que la rapidez c de los fotones de radiación electromagnéticos en el vacío son independientes de la escala.⁷​

La teoría de la física fractal requiere la presencia de ambas energías, la negativa y positiva.⁸​

Agujeros de gusano[editar]

Artículo principal: Agujeros de gusano

La energía negativa aparece en la teoría hipotética sobre los agujeros de gusano. Un agujero de gusano conecta directamente dos lugares que podrían estar separados arbitrariamente lejos, tanto en espacio como en tiempo, y en principio permite un viaje cercano e instantáneo entre ellos.⁹​

Curvatura (desplazamiento)[editar]

Artículo principal: Curvatura (desplazamiento)

Un principio teórico para un desplazamiento por curvatura o impulso de deformación para una astronave ha sido sugerido, involucrando la energía negativa. Comprometía una solución para la equación de Einstein sobre la relatividad general, en la cual una burbuja de espacio tiempo es movida rápidamente al expandir el espacio que hay detrás y al reducir el espacio delante de él.

energía potencial es la energía mecánica asociada a la localización de un cuerpo dentro de un campo de fuerzas (gravitatoria, electrostática, etc.) o a la existencia de un campo de fuerzas en el interior de un cuerpo (energía elástica). La energía potencial de un cuerpo es una consecuencia de que el sistema de fuerzas que actúa sobre el mismo sea conservativo.

Independientemente de la fuerza que la origine, la energía potencial que posee el sistema físico representa la energía "almacenada" en virtud de su posición y/o configuración, por contraposición con la energía cinética que tiene y que representa su energía debida al movimiento. Para un sistema conservativo, la suma de energía cinética y potencial es constante, eso justifica el nombre de fuerzas conservativas, es decir, aquellas que hacen que la energía "se conserve". El concepto de energía potencial también puede usarse para sistemas físicos en los que intervienen fuerzas disipativas, y que por tanto no conservan la energía, sólo que en ese caso la energía mecánica total no será constante, y para aplicar el principio de conservación de la energía es necesario contabilizar la disipación de energía.¹​

El valor de la energía potencial depende siempre del punto o configuración de referencia escogido para medirla, por esa razón se dice a veces que físicamente sólo importa la variación de energía potencial entre dos configuraciones.²​.

La energía potencial interviene como se ha mencionado en el principio de conservación de la energía y su campo de aplicación es muy general. Está presente no solo en la física clásica, sino también de la física relativista y física cuántica. El concepto se ha generalizado también a la física de partículas, donde se han llegado a utilizar potenciales complejos con el objeto de incluir también la energía disipada por el sistema.

Si bien la energía cinética (${\displaystyle E_{c}}$) de un cuerpo es una propiedad física que depende de su movimiento, la energía potencial (${\displaystyle E_{p}}$), en cambio, es un concepto de energía que va a depender del tipo de interacción que se ejerce sobre el cuerpo, de su posición y de la configuración en el espacio del citado cuerpo o cuerpos sobre los que se aplica. Así en una situación ideal en la que los objetos que constituyen el sistema físico en estudio estén ausentes de fricción, entonces la suma de ambas energías, cinética y potencial, va a representar la energía total del sistema, ${\displaystyle E}$, y se va a conservar, independientemente de la posición o posiciones que vaya ocupando el sistema en el tiempo.⁴​

La noción de energía potencial se relaciona con el trabajo realizado por las fuerzas sobre el sistema físico para trasladarlo de una posición a otra del espacio. La función energía potencial dependerá de forma importante del tipo de campo de fuerzas o interacción que actúe sobre el sistema. Por ejemplo, la fuerza de gravitación, la electromagnética, responsable de las interacciones eléctrica y magnética, o la elástica (derivada de la electromagnética). Si el trabajo no depende del camino seguido, entonces a la fuerza ${\displaystyle {\overrightarrow {F}}}$ se le llama conservativay el trabajo ${\displaystyle W}$ expresa la diferencia de energía potencial ${\displaystyle E_{p_{A}}-E_{p_{B}}}$ del sistema entre la posición de partida (A) y la posición de llegada (B).⁵​

${\displaystyle W_{AB}=\int _{B}^{A}{\overrightarrow {F}}\cdot \,{\overrightarrow {dl}}=E_{p_{A}}-E_{p_{B}}\qquad \qquad }$

También se utiliza la función potencial ${\displaystyle V}$ en lugar de la energía potencial ${\displaystyle E_{p}}$ para representar el trabajo realizado por la unidad básica de la interacción. Si, por ejemplo, la interacción es la gravitatoria, sería la unidad de masa y en el caso de la interacción eléctrica, la unidad de carga.

La función energía potencial y, en especial, la función potencial, tienen gran interés en la física no solo cuando se aplican a las interacciones que son importantes a nuestra escala, como son la gravitatoria, la electromagnética y la elástica (derivada de la electromagnética), sino también cuando se estudia cualquier tipo de fuerza o interacción, incluso en la física cuántica al tratar de resolver la dinámica de un sistema físico mediante la ecuación de Schrödinger.⁶​ Se aplica, por ejemplo, a la física atómica en la obtención de los estados electrónicos del átomo o en la física molecular, para la obtención de los estados electrónicos, de vibración, de vibración-rotación y de rotación de la molécula, así como en la física del estado sólido. También se aplica en la física nuclear.⁷​

En otras formulaciones más generales de la física, la función potencial juega, así mismo, un papel importante. Entre ellas, las formulaciones lagrangiana y hamiltoniana de la mecánica.⁸​

Energía potencial gravitatoria[editar]

Los coches de una montaña rusa alcanzan su máxima energía potencial gravitacional en la parte más alta del recorrido. Al descender, esta se convierte en energía cinética, llegando a ser máxima al alcanzar el punto más bajo de su trayectoria (y la energía potencial mínima). Luego, al volver a elevarse debido a la inercia del movimiento, el traspaso de energías se invierte. Si se asume una fricción insignificante, la energía total del sistema permanece constante

Artículo principal: Energía potencial gravitatoria

La energía potencial gravitatoria se define como la energíaque poseen los cuerpos por el hecho de poseer masa y estar situados a una determinada distancia mutua. Entre las masas de grandes magnitudes se ejercen fuerzas de atracción, de mayor intensidad cuanto mayores son estas. Aplicado, por ejemplo, al movimiento planetario, la masa mayor es la del sol que crea un campo de fuerzas gravitatorio que actúa sobre las masas menores de los planetas. A su vez, cada planeta crea un campo de fuerzas gravitatorio que actúa sobre las masas menores que estén próximas al planeta, los satélites.⁹​

El trabajo realizado para llevar una masa de prueba m en presencia de otra masa M, fuente del campo gravitatorio, desde un punto A a otro B, es la diferencia de la energía potencial de la masa m en el punto de partida A menos la energía potencial en el punto de llegada B. El citado trabajo no depende del camino seguido sino tan solo de los puntos inicial y final. Al gozar de esta propiedad la fuerza gravitatoria y el campo gravitatorio (la fuerza gravitatoriasobre la unidad de masa), al campo se le llama campo conservativo y tiene pleno sentido obtener el potencial gravitatorio, derivado del campo creado por la masa M, así como la energía potencial gravitatoria derivada de la fuerza gravitatoria entre las masas m y M.

Si se considera una masa M en el origen del sistema de coordenadas como fuente del campo gravitatorio y se elige como referencia el infinito, punto en el que cualquier masa m tiene una energía potencial nula, la energía potencial es el trabajo necesario para llevar la masa m desde el infinito hasta un determinado punto A definido por la coordenada ${\displaystyle r}$ (la distancia del punto A al origen de coordenadas).⁹​

${\displaystyle W=E_{p_{A}}-E_{p_{\infty }}=}$ ${\displaystyle \Delta E_{p}=-\int _{\infty }^{A}F_{g}\cdot \,dr=-\int _{\infty }^{A}{\frac {G\cdot M\cdot m}{r^{2}}}\cdot \,dr=G\cdot M\cdot m\cdot \left\lbrack {\frac {1}{r}}\right\rbrack _{\infty }^{A}={\frac {G\cdot M\cdot m}{r_{A}}}=E_{p_{A}}\qquad \qquad [1]}$

Donde: ${\displaystyle E_{p}}$ es la energía potencial gravitatoria de la masa ${\displaystyle m}$, cuyo valor depende de la distancia ${\displaystyle r}$ entre la masa de prueba ${\displaystyle m}$ y la masa ${\displaystyle M}$ que genera el campo gravitatorio, y se mide en julios (${\displaystyle J}$). Por otro lado, ${\displaystyle F_{g}={\frac {G\cdot M\cdot m}{r^{2}}}}$ es la fuerza gravitatoria sobre la masa de prueba ${\displaystyle m}$ situada a una distancia ${\displaystyle r}$ de la masa ${\displaystyle M}$que crea el campo gravitatorio y se mide en newtons (${\displaystyle N}$). Además, ${\displaystyle G}$ es la constante de gravitación universal, cuyo valor es ${\displaystyle G=6.673\times 10^{-11}\;\left({\cfrac {{\text{N}}\cdot {\text{m}}^{2}}{{\text{kg}}^{2}}}\right)}$. Finalmente, ${\displaystyle M}$ y ${\displaystyle m}$ se miden en kilogramos (${\displaystyle kg}$) ${\displaystyle R}$ es la distancia que separa las dos masas, medida en metros (${\displaystyle m}$)

La ecuación [1] que representa la energía potencial ${\displaystyle E_{p_{A}}}$ de las masas m y M cuando están separadas una distancia ${\displaystyle r_{A}}$, es aplicable tanto a masas puntuales como a masas con simetría esférica, siendo la distancia entre ellas, la que hay entre los centros de dichas esferas.

La energía potencial cerca de la superficie de la Tierra[editar]

La energía potencial que posee una masa ${\displaystyle m}$ situada a una altura ${\displaystyle h}$ sobre la superficie terrestre vale:

${\displaystyle \Delta E_{p}=m\cdot g\cdot h\qquad \qquad [2]}$

Esta expresión es un caso particular de la ecuación anterior [1]. Dicho caso se presenta cuando la masa se encuentra a una altura pequeña sobre la superficie de la tierra. Para demostrarlo, basta con aplicar la expresión [1] y considerar la variación de energía potencial entre las alturas sobre la superficie de la tierra, ${\displaystyle h_{1}}$ y ${\displaystyle h_{2},(h_{1}\ll R_{t},h_{2}\ll R_{t}}$ y ${\displaystyle h_{2}>h_{1})}$ siendo ${\displaystyle R_{t}}$ el radio de la tierra.¹⁰​

${\displaystyle \Delta E_{p}=E_{p2}-E_{p1}=G\cdot M\cdot m\cdot \left({\frac {1}{R_{t}+h_{1}}}-{\frac {1}{R_{t}+h_{2}}}\right)=}$ ${\displaystyle =E_{p2}-E_{p1}=G\cdot M\cdot m\cdot {\frac {(h_{2}-h_{1})}{R_{t}^{2}+R_{t}\cdot (h_{2}+h_{1})+h_{1}\cdot h_{2}}}\approx G\cdot M\cdot m\cdot {\frac {h_{2}-h_{1}}{R_{t}^{2}}}\qquad \qquad [3]}$

En este caso, los productos ${\displaystyle R_{t}\cdot h_{2},R_{t}\cdot h_{1}}$ y ${\displaystyle h_{1}\cdot h_{2}}$ son muy pequeños comparados con ${\displaystyle R_{t}^{2}}$ y, por lo tanto, se pueden despreciar en la ecuación [3].

Llamando ${\displaystyle g=G\cdot M\cdot {\frac {1}{R_{t}^{2}}}}$

${\displaystyle E_{p2}-E_{p1}=m\cdot g\cdot (h_{2}-h_{1})}$

Si se toma ${\displaystyle h_{1}}$ como el origen de energías potenciales, por ejemplo, al nivel del mar y llamando ${\displaystyle h_{2}=h}$:

${\displaystyle \Delta E_{p}=m\cdot g\cdot h}$

Del desarrollo anterior se deduce que para ${\displaystyle h\ll R_{t}}$ la aproximación última es adecuada.

Velocidad de escape[editar]

La velocidad de escape es la velocidad mínima necesaria para que un cuerpo de masa ${\displaystyle m}$ salga fuera de la atracción gravitatoria.¹¹​

La fuerza de gravitación es conservativa. La energía potencial ${\displaystyle E_{p}(r)}$ de una masa ${\displaystyle m}$ es:

${\displaystyle E_{p}(r)=-G\cdot {\frac {m\cdot M}{r}}}$

Para que el cuerpo escape a la acción del campo gravitatorio la energía total ${\displaystyle E_{t}}$ del mismo debe ser positiva o nula, es decir, debe suceder que la energía cinética supere o, al menos iguale, la energía potencial. En el caso umbral estaremos calculando la velocidad de escape.¹²​ Se puede calcular en el caso de la Tierra.

${\displaystyle E_{T}=0}$

${\displaystyle E_{t}=E_{c}+E_{p}=0\Rightarrow {\frac {1}{2}}\cdot m\cdot v_{e}^{2}=G\cdot {\frac {m\cdot M}{r}}}$

${\displaystyle v_{e}={\sqrt {\frac {2\cdot G\cdot M}{r}}}={\sqrt {2gr}}}$ ${\displaystyle (m/s)}$

donde ${\displaystyle r}$ es la distancia radial o posición del cuerpo de masa ${\displaystyle m}$ con respecto a la masa ${\displaystyle M}$ que genera el campo gravitatorio¹³​

Velocidad de escape de la superficie de la Tierra

${\displaystyle G=6.674\cdot 10^{-11}\;{\cfrac {{\text{N}}\cdot {\text{m}}^{2}}{{\text{kg}}^{2}}}}$

${\displaystyle M_{T}=5,97\cdot 10^{24}}$ ${\displaystyle kg}$

${\displaystyle R=6,37\cdot 10^{6}}$ ${\displaystyle m}$

Sustituyendo los datos se obtiene:¹⁴​

${\displaystyle v_{e}={\sqrt {\frac {2\cdot G\cdot M_{T}}{R}}}={\sqrt {\frac {2\cdot 6,67\cdot 10^{-11}\cdot 5,97\cdot 10^{24}}{6,37\cdot 10^{6}}}}\approx 11,17\cdot 10^{3}}$${\displaystyle m\cdot s^{-1}}$

Si el móvil supera la velocidad de escape abandonaría todavía con más facilidad la acción del campo gravitatorioterrestre.

Superficies equipotenciales[editar]

El potencial gravitatorio se define como la energía potencial por unidad de masa:

${\displaystyle V={\frac {E_{p}}{m}}}$

Y por tanto se obtiene:

${\displaystyle V(r)={\frac {G\cdot M}{r}}}$

Donde ${\displaystyle V}$ es la energía potencial de la unidad de masa, o potencial, a una distancia ${\displaystyle r}$ de la masa ${\displaystyle M}$. Las unidades de ${\displaystyle V}$ en el S.I. son ${\displaystyle {\frac {J}{kg}}}$.

G es la constante de gravitación universal.

M es la masa del objeto que crea el campo y, por tanto, estará medida en ${\displaystyle kg}$.

Si M es puntual o de geometría esférica, las superficies equipotenciales (superficies de potencial constante) son la familia de esferas definidas por la familia de superficies:

${\displaystyle V_{i}={\frac {G\cdot M}{r_{i}}}=C_{i}\ ,\qquad i=1,2,3...}$

siendo ${\displaystyle C_{i}}$ constantes arbitrarias cuyo valor numérico representa el potencial gravitatorio asociado a cada valor de la posición ${\displaystyle r_{i}}$.

Las superficies equipotenciales gravitatorias terrestres son todas las esferas con centro en el de la Tierra.

Ejemplos de la energía potencial gravitatoria[editar]

Animación de una bola en una montaña rusa

Montaña Rusa[editar]

El dibujo de una montaña rusa en un plano se puede interpretar como la representación de la función energía potencial ${\displaystyle E_{p}}$ de un cuerpo en el campo gravitatorio. Cuanto más sube un móvil la montaña rusa, mayor es su energía potencial y menor su energía cinética ${\displaystyle E_{c}}$, y por tanto se desplaza más lento. En los máximos relativos de dicha función (los picos de la montaña rusa) su energía potencial será más elevada que en los puntos de su entorno. Estos puntos se llamarán puntos de equilibrio mecánico inestable, ya que si se deposita en ellos un objeto con ${\displaystyle v=0}$ por poco que se desplace de ese punto, el objeto siempre tenderá a alejarse. Por otro lado, si lo situamos en los mínimos de la función (los valles de la montaña rusa), el móvil que los abandonase en uno u otro sentido siempre tenderá a volver hacia ellos, son los puntos llamados puntos de equilibrio estable.¹⁵​ Como la energía mecánica ${\displaystyle E}$ del cuerpo se conserva ${\displaystyle E=E_{c}+E_{p}=E_{cmax}=E_{pmax}}$ , en la figura.

Péndulo[editar]

En el caso de un péndulo, cuyo movimiento puede alcanzar una altura ${\displaystyle h}$ medida a partir de su posición más baja, también se puede comprobar la ley de conservación de la energía. En los puntos más altos (altura h), donde la energía potencial es máxima, la velocidad del péndulo es nula y el movimiento cambia de sentido. Por otro lado, la posición más baja, que se pude llamar ${\displaystyle P}$, será aquella con una mayor energía cinética y velocidad máxima pero con una energía potencial mínima. La posición ${\displaystyle P}$ se podrá tomar como origen de la energía potencial (se le puede asociar una energía potencial nula).

Animación de un péndulo que alcanza una altura h

Aplicación al movimiento planetario[editar]

El diagrama de energía potencial gravitatoria de los planetas permite determinar la forma de su trayectoria en torno al sol. Para una energía media, que corresponda a la región del pozo de potencial, la trayectoria del planeta es una elipse de radios r1 y r2 (primera ley de Kepler)

La energía potencial gravitatoria influye en la forma de las órbitas de los planetas y otros cuerpos celestes del Sistema Solar.¹⁶​ El tipo de órbita es una cónica y su forma dependerá de la energía mecánica total ${\displaystyle E}$ del cuerpo.¹⁷​ La energía potencial es negativa o positiva, mientras que la energía cinética es siempre positiva.

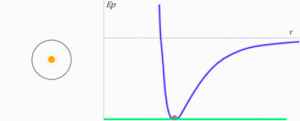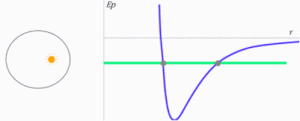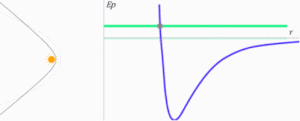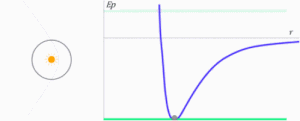
La energía total del cuerpo, al ser la suma de ambas, puede ser negativa, positiva o nula. Es fácil reconocer la forma de las órbitas con ayuda del diagrama de energía potencial ${\displaystyle E_{p}(r)}$ o el de potencial ${\displaystyle V(r)}$. La línea verde sirve para indicar en cada caso cuál es el valor de la energía total del planeta o el cuerpo celeste en la animación que sigue. El Sol se encuentra siempre en la posición ${\displaystyle r=0}$, y representa el origen de la fuerza gravitatoria.¹⁶​

El diagrama de energía potencial gravitatoria de los cuerpos celestes de un sistema solar permite determinar la forma de su trayectoria en torno a la estrella. La animación describe las diferentes trayectorias del cuerpo celeste, en función de su energía total, alrededor de su sol

• Si la energía total es negativa y de valor absoluto igual a la mitad de la energía potencial (mínimo de la curva), la trayectoria es una circunferencia con centro en el origen de las fuerzas.

${\displaystyle {\color {Black}E}={\color {Black}-{\frac {1}{2}}G{\frac {Mm}{r}}}}$

• Si la energía total es mayor que la que se necesita para que la órbita sea circular, pero aun así permanece negativa, la órbita pasa a ser una elipse exterior a la órbita circular. En este caso, el centro de fuerzas será uno de los focos de dicha elipse.

${\displaystyle {\color {Black}-{\frac {1}{2}}G{\frac {Mm}{r}}}<{\color {Black}E}<{\color {Black}0}}$

• Si la energía total es menor que la necesaria para describir una órbita circular, no existirá el movimiento al resultar una energía cinética negativa.

${\displaystyle {\color {Black}E}<{\color {Black}-{\frac {1}{2}}G{\frac {Mm}{r}}}\qquad no\ es\ posible}$

• Si la energía total llega a ser cero o positiva, la trayectoria deja de ser cerrada y el cuerpo escapará de la atracción gravitatoria ejercida por M. Si ${\displaystyle E=0}$, la energía cinética es, en valor absoluto, igual a la energía potencial. Representa la mínima energía necesaria para que el cuerpo escape de dicha atracción alcanzando, entonces, la velocidad de escape y su trayectoria será una parábola con su foco en el centro de fuerzas.¹⁸​ La trayectoria será, pues, abierta.

${\displaystyle {\color {Black}E}=0\Rightarrow E_{c}=-E_{p}}$

• Si la energía total es positiva es porque en valores absolutos su energía cinética es mayor que su energía potencial. Por lo tanto, su velocidad excede la velocidad de escape y su trayectoria será una hipérbola, una cónica también abierta.

${\displaystyle {\color {Black}E}>0\Rightarrow E_{c}>-E_{p}}$

Energía potencial elástica[editar]

Esta catapulta hace uso de la energía potencial elástica

Artículo principal: Energía potencial elástica

La elasticidad es una propiedad de ciertos materiales por la que, una vez deformados, estirados o separados de su posición inicial, pueden recuperar su estado original, o de equilibrio. Las fuerzas restauradoras responsables de la recuperación son las fuerzas elásticas como en el caso de los muelles, las tiras de goma o las cuerdas de instrumentos musicales. Muchas máquinas de guerra de la antigüedad utilizaban este tipo de energía para lanzar objetos a distancia como, por ejemplo, el arco que dispara una flecha, la ballesta o la catapulta. Las vibraciones u oscilaciones de los objetos materiales, ocasionadas por las fuerzas elásticas, son la fuente de las ondas sonoras. Las fuerzas recuperadoras, cuando el objeto recupera su forma original sin apenas amortiguamiento o deformación, son conservativas y se puede derivar una energía potencial elástica, que sumada a la energía cinética, permite obtener la energía mecánica del objeto.⁹​

Se dice que un material es más elástico cuando vuelve a su posición de equilibrio de manera más precisa. Una tira de goma es fácil de estirar, y se retorna de nuevo cerca de su longitud original cuando se libera, pero no es tan elástica como una cuerda de guitarra. La cuerda de guitarra es más difícil de estirar, pero posee mejor recuperación que la tira de goma, porque retorna a su longitud original de manera más precisa.¹⁹​

Un muelle es un ejemplo de objeto elástico que recupera su forma original de forma precisa: cuando se estira ejerce una fuerza elástica que tiende a devolverle a su longitud original. Se comprueba experimentalmente que esta fuerza restauradora es proporcional a la longitud estirada del muelle. La forma de expresar esta proporcionalidad entre la fuerza y la cantidad estirada es por medio de la ley de Hooke. El coeficiente de proporcionalidad en esta deformación depende del tipo de material y de la forma geométrica que se considere. Para sólidos, la fuerza elástica se describe generalmente, en términos de la cantidad de deformación, ocasionada por la fuerza de tensión resultante de un estiramiento determinado, llamado módulo de elasticidad o de Young. Para líquidos y gases se expresa por la variación de presión capaz de producir una variación del volumen y se denomina módulo de compresibilidad. Para muelles y cables se emplea una constante elástica k.²⁰​

La ley de Hooke describe aproximadamente las propiedades elásticas de los cuerpos y en la que se basan las condiciones elásticas de respuesta, cerca de las condiciones de equilibrio, del material deformable sujeto a un estiramiento o compresión. Tiene numerosas aplicaciones y en todas ellas la fuerza responsable se obtiene con la citada ley de manera aproximada, y el movimiento de respuesta resultante es el del oscilador armónico.²¹​

Ley de Hooke[editar]

Representación de la ley de Hooke en una bola moviéndose en una superficie sin rozamiento.

Una de las propiedades de la elasticidad de un sólido o de un fluido, al estirarse o deformarse, es que dicho estiramiento o deformación es proporcional a la fuerza aplicada. Es decir, se necesitaría una fuerza doble para producir un estiramiento doble. Esa dependencia lineal del desplazamiento con la fuerza aplicada es conocida como la Ley de Hooke.²⁰​

Robert Hooke fue un científico inglés tanto teórico como experimental, polemista incansable, con un genio creativo de primer orden, que formó parte del núcleo creador de la Royal Society. En 1660, mientras trabajaba como ayudante de Robert Boyle, formuló lo que hoy se denomina Ley de Elasticidad de Hooke. Si se aplica esta ley a una masa que está sujeta a un muelle, estirándolo una longitud x de su posición de equilibrio, la ley de Hooke establece que el bloque estará entonces sujeto a una fuerza elástica de recuperación de la forma:

${\displaystyle {\vec {F_{el}}}=-kx{\vec {u_{x}}}}$,

siendo k la constante elástica del muelle y x el desplazamiento sufrido respecto de su posición de equilibrio x=0. El signo menos de la ecuación refleja que la fuerza elástica es una fuerza restauradora que tiende siempre a llevar al sólido a su posición de equilibrio, en este caso x=0.²²​

Deducción de la energía potencial elástica[editar]

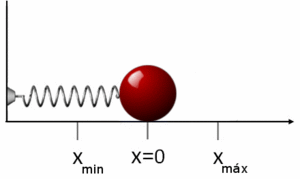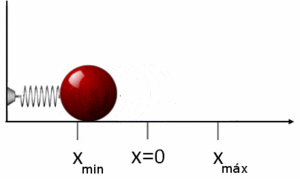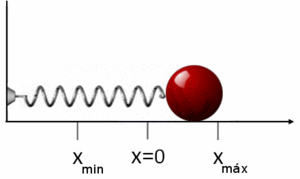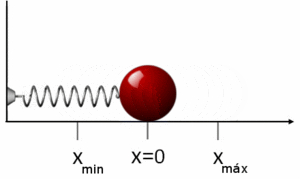
Si se coloca una masa m sujeta a un extremo del muelle y se separa una distancia x de su posición de equilibrio, x=0, este comenzará a oscilar con un movimiento armónico simple. En este movimiento el bloque posee una energía cinética y una energía potencial. Al ser la fuerza elástica que satisface la ley de Hooke una fuerza conservativa, se puede derivar la función energía potencial, bajo la acción de la fuerza elástica del muelle. Así, el trabajo realizado para estirar el muelle una distancia x desde su posición de equilibrio, oponiéndose a la fuerza del muelle es:²³​

${\displaystyle W=E_{p}(x)=\int _{0}^{x}-F_{x}dx=\int _{0}^{x}-(-kx)dx={\frac {1}{2}}kx^{2}\qquad \qquad }$

Este trabajo representa la energía potencial Ep que tiene el bloque en la posición x. Para ello se ha convenido en asociar la E_p = 0 a la posición x=0 (origen de la función potencial). Si ahora se calcula el trabajo para desplazar el bloque de una posición ${\displaystyle x_{1}}$ a otra ${\displaystyle x_{2}}$, se comprueba que este solo depende de las posiciones inicial y final:²³​

${\displaystyle W=E_{p}(x_{2})-E_{p}(x_{1})=\int _{x_{1}}^{x_{2}}-kxdx={\frac {1}{2}}k(x_{1}^{2}-x_{2}^{2})}$

En la figura se puede observar la función energía potencial Ep (x) como una parábola centrada en x=0, función de la posición x. La recta de pendiente -k, es la fuerza elástica correspondiente ${\displaystyle {\vec {F_{el}}}=-kx{\vec {u_{x}}}}$. A la vez se representa la cantidad estirada del muelle en función de su posición x. Si con una fuerza F se produce un desplazamiento x, con la fuerza 2F el desplazamiento es también el doble, 2x. La parte negativa del eje x representa el desplazamiento de la masa cuando el muelle está comprimido.

Curva de energía potencial elástica y fuerza correspondiente aplicado a la respuesta de una bola sujeta a un muelle

Propiedades de la curva de energía potencial[editar]

• Pendiente de la curva ${\displaystyle E_{p}(x)}$ :

${\displaystyle Fuerza:{\vec {F}}=-{\frac {dE_{p}}{dx}}\ {\vec {u_{x}}}=-kx{\vec {u_{x}}}}$

Si ${\displaystyle x>0}$

${\displaystyle {\frac {dE_{p}}{dx}}=kx>0\quad 'pendiente\quad positiva'}$

Si ${\displaystyle x<0 annotation="">$

${\displaystyle {\frac {dE_{p}}{dx}}=kx<0 annotation="" negativa="" pendiente="" quad="">$

• Punto de equilibrio:

${\displaystyle {\frac {dE_{p}}{dx}}=kx=0\Rightarrow x=0}$

${\displaystyle {\frac {d^{2}E_{p}}{dx^{2}}}=k>0}$ es un mínimo

Energía potencial electrostática y potencial eléctrico[editar]

Artículo principal: Energía potencial electrostática

La variación de la energía potencial representa un trabajo realizado por una fuerza conservativa. Del mismo modo que la fuerza de atracción entre dos masas es conservativa, también la fuerza eléctrica o fuerza de Coulomb ${\displaystyle F_{el}}$ entre dos cargas es conservativa, siendo de repulsión si tienen el mismo signo y de atracción si son de signo opuesto. Los objetos que se repelen tienen mayor energía potencial cuanto menor es la distancia entre ellos, y si se atraen es mayor su energía potencial cuanto mayor es la distancia entre ellos, como veremos a continuación.

El trabajo de una fuerza conservativa es igual a la diferencia entre el valor inicial y el valor final de una función, la energía potencial, dado que solamente dependerá de las posiciones inicial y final y no de la trayectoria seguida. Las fuerzas electrostáticas originadas por cargas eléctricas son conservativas y el trabajo realizado por estas fuerzas no dependerá de la trayectoria seguida:

${\displaystyle W=\int _{A}^{B}{\vec {F}}_{el}\cdot d{\vec {l}}=E_{pA}-E_{pB}\,\!}$

siendo ${\displaystyle E_{p}}$ la función energía potencial y ${\displaystyle E_{pA}}$ y ${\displaystyle E_{pB}}$ los valores de la energía potencial en las posiciones A y B.²⁴​

Variables implicadas en el trabajo eléctrico realizado al trasladar una carga q, en presencia campo eléctrico creado por otra carga Q

Para calcular el trabajo ${\displaystyle W}$ debido a la fuerza eléctrica o electrostática, ${\displaystyle F_{el}}$:

${\displaystyle {\overrightarrow {F}}_{el}={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Qq}{r^{2}}}{\overrightarrow {u}}=q{\overrightarrow {E}}}$

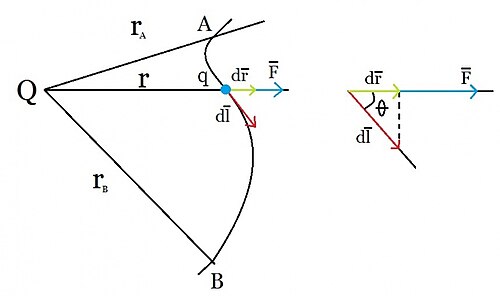
Para trasladar la carga ${\displaystyle q}$ de la posición A a la B se necesita primero expresar el trabajo infinitesimal ${\displaystyle dW}$ como el producto escalar del vector fuerza ${\displaystyle {\vec {F}}_{el}}$ por el vector desplazamiento ${\displaystyle {\vec {dl}}}$ tangente a la trayectoria. Además, la fuerza eléctrica sobre la carga q es ${\displaystyle {\vec {F}}_{el}=q{\vec {E}}}$, siendo ${\displaystyle {\vec {E}}}$ el campo eléctrico debido a la carga Q. De este modo, el trabajo elemental ${\displaystyle dW}$ se puede escribir: ²⁵​

${\displaystyle dW={\vec {F}}_{el}\cdot {\vec {dl}}=F_{e}dlcos\theta =F_{e}dr=qEdr}$

siendo dr es el desplazamiento infinitesimal de la carga q en la dirección radial desde Q y la constante ${\displaystyle \varepsilon _{0}}$representa la permitividad eléctrica del vacío.

Así, el trabajo ${\displaystyle W}$ debido a la fuerza eléctrica entre las cargas Q y q se puede considerar como el realizado por el campo eléctrico E creado por la carga Q para trasladar la carga q, desde una posición A a otra B, una vez que se ha expresado la fuerza eléctrica en función del campo eléctrico creado por una de ellas, en este caso Q. Y será, entonces:²⁵​

${\displaystyle W=\int _{A}^{B}{\vec {F}}_{el}\cdot d{\vec {l}}=\int _{A}^{B}q{\vec {E}}\cdot d{\vec {l}}=\int _{A}^{B}{\frac {Qq}{4\pi \varepsilon _{0}r^{2}}}dr=-\left\lbrack {\frac {Qq}{4\pi \varepsilon _{0}r}}\right\rbrack _{A}^{B}={\frac {Qq}{4\pi \varepsilon _{0}r_{A}}}-{\frac {Qq}{4\pi \varepsilon _{0}r_{B}}}}$

El trabajo W debido a la fuerza electrostática no depende del camino seguido por la carga q para ir desde la posición A a la posición B, ya que solo depende de las posiciones inicial ra y final rb. Esto es debido a que la fuerza de repulsión Fel, que ejerce la carga fuente Q situada en el origen de coordenadas sobre la carga q, es conservativa. Es más, este trabajo realizado por la fuerza electrostática es la diferencia de los valores que adquiere una función entre las posiciones de partida y llegada. Esta función es, precisamente la energía potencial para la fuerza y el campo eléctrico y se escribe como:²⁶​

${\displaystyle E_{p}(r)={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Qq}{r}}}$

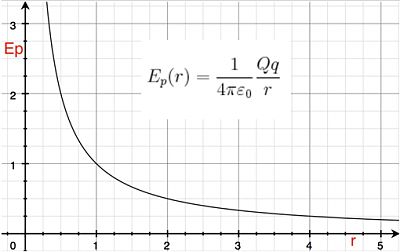
La fuerza electrostática que da origen a la energía potencial entre las dos cargas es de carácter repulsivo si las cargas Q y q son del mismo signo (como en el caso indicado). La energía potencial será, por tanto, una función decreciente con r siguiendo la función .${\displaystyle +1/r}$ Si las cargas fueran de signo opuesto la energía potencial sería negativa, siguiendo la función ${\displaystyle +1/r}$ y la fuerza electrostática de carácter atractivo. Esta dualidad, en el carácter repulsivo o atractivo de la fuerza electrostática y del diferente signo de la energía potencial y del potencial (por extensión), es una propiedad intrínseca a la interacción eléctrica, que no posee otro tipo de campos o de fuerzas como, por ejemplo, la fuerza de gravitación.

Si se utilizan las funciones energía potencial y potencial es necesario establecer un origen de potenciales como referencia de nivel cero para dichas funciones. Considerando cargas puntuales, el valor cero de energía potencial se establece en el infinito (donde la energía potencial y el potencial se anulan), o sea para ${\displaystyle r=\infty }$, ${\displaystyle E_{p}=0}$quedando definida la función energía potencial para todos los puntos del espacio, sin necesidad de ninguna constante adicional. Habitualmente se utilizan diferencias de energía potencial (o de potencial) y, por tanto, el trabajo realizado por la fuerza conservativa, no dependerá del origen de potenciales.

Gráfica en la que se puede comprobar como disminuye el valor de Ep(r) al aumentar la separación entre ambas cargas siguiendo la ley ${\displaystyle {\frac {1}{r}}}$

Para definir de manera natural el potencial eléctrico a partir de la energía potencial electrostática, se considera la energía potencial de la carga Q y la carga q= +1 Coul separadas una distancia r cuando el campo eléctrico E lo crea la carga fuente Q. De esta forma, se obtendrá el potencial V creado por la carga Q y que representa, a su vez, la energía potencial referida a la unidad de carga positiva. Por tanto, basta con dividir la energía potencial, Ep (r) por la carga q, que se sitúa a una distancia r de la carga fuente Q, para obtener el potencial eléctrico creado por Q a una distancia r:²⁶​

${\displaystyle V(r)={\frac {E_{p}(r)}{q}}={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r}}\qquad \qquad [1]}$

estando la carga fuente Q en el origen de coordenadas. El potencial eléctrico tiene el mismo comportamiento con la distancia r que la energía potencial eléctrica.

Potencial creado por una carga puntual Q

El hecho de que la fuerza electrostática sea conservativa significa que la energía cinética más la energía potencial asociada a la partícula de carga q y de masa m es una constante, es decir, su energía total E permanece constante para cualquier posición r adoptada por la partícula dentro de la región donde aparece el campo creado por Q:

${\displaystyle E={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Qq}{r}}+{\frac {mv^{2}}{2}}=constante}$

Potencial debido a un sistema de cargas puntuales[editar]

Se puede calcular el potencial en un punto P debido a la presencia de un sistema de n cargas puntuales por medio de la superposición del creado por cada carga, sobre una dada, de manera independiente del resto. El potencial es una magnitud escalar a la que se puede aplicar el principio de superposición por ser lineales las ecuaciones de la electrostática.

• El potencial creado por una carga ${\displaystyle q}$ a una distancia r viene dado por

${\displaystyle V={\frac {1}{4\pi \varepsilon _{0}}}{\frac {q}{r}}}$

• El potencial creado por varias cargas ${\displaystyle q_{1},q_{2},q_{3},...q_{i}}$ en un punto P que distan ${\displaystyle r_{1},r_{2},r_{3},...r_{i}}$ de cada centro de carga respectivamente, será la superposición de los potenciales que crean cada una de las cargas, por separado, en dicho punto

${\displaystyle V=V_{1}+V_{2}+V_{3}+...+V_{i}=\sum _{i}^{}{\frac {1}{4\pi \varepsilon _{0}}}{\frac {q_{i}}{r_{i}}}={\frac {1}{4\pi \varepsilon _{0}}}\sum _{i}^{}{\frac {q_{i}}{r_{i}}}}$

El potencial debido a una distribución continua de carga se puede calcular transformando la última expresión. Las cargas puntuales pasan a ser elementos de carga infinitesimales dq y la suma pasa a ser una integral

${\displaystyle V={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {dq}{r}}}$

Esta expresión supone que V=0 a una distancia infinita de distribución. No puede, por tanto, utilizarse para obtener el potencial creado por las distribuciones indefinidas de carga como pueden ser la distribución lineal de carga indefinida o el plano indefinido de carga. En toda región del espacio donde existe un campo eléctrico, existe también una energía potencial electrostática expresable como

${\displaystyle E_{p}={\frac {\varepsilon _{0}}{2}}\int {\vec {E}}^{2}dV\qquad \qquad [2]}$

extendida al volumen del espacio donde reside el campo eléctrico. Y siendo ${\displaystyle {\vec {E}}^{2}={\vec {E}}.{\vec {E}}=E^{2}}$ (definición de producto escalar de dos vectores).

Superficies equipotenciales[editar]

Una forma práctica de visualizar en el espacio la energía potencial o el potencial consiste en utilizar la representación gráfica de las superficies equipotenciales o superficies de igual potencial. La definición matemática de superficie equipotencial aplicado a la energía potencial es:

${\displaystyle E_{p}=cte}$

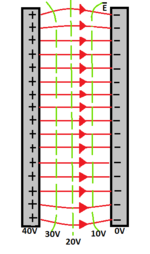
Una superficie equipotencial representa el lugar geométrico de todos los puntos del espacio que presentan el mismo valor de potencial y, por tanto, la misma energía potencial. Para una carga puntual, las superficies equipotenciales son esferas concéntricas en cuyo centro está la carga. Por otro lado, las líneas de campo son radiales y perpendiculares a las superficies esféricas. Para un campo eléctrico uniforme las superficies equipotenciales son planos paralelos entre sí y perpendiculares a las líneas de campo.²⁷​

Si una carga eléctrica que se desplaza a lo largo de una superficie equipotencial no experimenta cambios de energía potencial, ni por tanto, del potencial. Es decir,

${\displaystyle dV={\vec {E}}.d{\vec {l}}=0}$

Algunas propiedades de las superficies equipotenciales son:²⁸​

• Las líneas de campo eléctrico son, en cada punto, perpendiculares a las superficies equipotenciales con sentido hacia los potenciales decrecientes.
• El trabajo para desplazar una carga entre dos puntos de una misma superficie equipotencial es nulo.
• Dos superficies equipotenciales no se pueden cortar.

Cuando la representación geométrica de los potenciales se realiza en el plano, en lugar de superficies equipotenciales aparecen líneas equipotenciales. Ahora las líneas de campo eléctrico serán perpendiculares a las líneas equipotenciales.²⁶​

1.- Líneas de campo y líneas equipotenciales (LE) creadas por una carga positiva. Las (LE) son circunferencias; en tres dimensiones son superficies esféricas

2.- Líneas de campo y líneas equipotenciales (LE) creadas por un campo uniforme. Las (LE) son líneas rectas; en tres dimensiones son planos

3.- Líneas de campo y líneas equipotenciales (LE) creadas por un dipolo eléctrico. En tres dimensiones las (LE) forman superficies equipotenciales

Aplicaciones[editar]

En verde, corte de las superficies equipotenciales con un plano perpendicular a las placas del condensador plano. Líneas del campo eléctrico en rojo.

Algunas aplicaciones de la energía potencial en el campo de la electrostática son:

Los condensadores[editar]

Un condensador es un dispositivo que almacena la energía en forma de energía potencial electrostática en su interior. Para almacenar la carga eléctrica, creadora del campo eléctrico, utiliza dos superficies conductoras en forma generalmente de láminas o placas separadas por un material dieléctrico (aislante). Estas placas son las que se cargarán eléctricamente cuando se conecte a una fuente de alimentación. Las dos placas se cargarán con la misma cantidad de carga (q) pero con distintos signos, siendo la magnitud de la carga proporcional a la diferencia de potencial aplicada. La constante de proporcionalidad entre la carga adquirida por el condensador y la diferencia de potencial alcanzado entre las dos placas se conoce como capacidad del condensador:

${\displaystyle C={\frac {q}{V}}}$

Donde ${\displaystyle q}$ es la carga de una de las placas y ${\displaystyle V}$ la diferencia de potencial entre ellas.

Un condensador cargado con una carga ${\displaystyle q}$ y aislado, representa un sistema que mantiene un campo eléctrico ${\displaystyle E}$ en su interior y, por tanto, almacena, en los lugares donde está presente el campo, una energía electrostática de origen 'potencial'. La expresión de esta energía potencial electrostática se puede representar en tres formas directas equivalentes. En dos de ellas aparece directamente la expresión de la diferencia de potencial ${\displaystyle V}$ entre sus armaduras:²⁹​

${\displaystyle E_{p}={\frac {1}{2}}\varepsilon _{0}\int E^{2}dV={\frac {1}{2}}qV={\frac {1}{2}}{\frac {q^{2}}{C}}={\frac {1}{2}}CV^{2}}$

Las aplicaciones de los condensadores son numerosas en el campo de la electrónica y por tanto, también lo son para los electrodomésticos de consumo. En las aplicaciones tecnológicas de hoy en día están presentes en los dispositivos multimedia como ordenadores, teléfonos móviles, reproductores de vídeo y de sonido, etc. En estas aplicaciones de la tecnología actual, los condensadores son capaces de almacenar una energía potencial electrostática durante breves espacios de tiempo y con valores no excesivamente elevados.³⁰​

El generador de Van de Graaff[editar]

Esquema del Generador de Van de Graaff

En 1931 Van de Graaff contruyó el mayor generador electrostático del mundo con el propósito de producir una diferencia de potencial muy alta (del orden de 20 millones de voltios) y poder acelerar partículas cargadas que se hacían chocar contra blancos fijos. Los resultados de las colisiones permitían informar sobre las características de los núcleos atómicos del material que constituye el blanco.³¹​

Un generador Van de Graaff consta de:

• Un generador inferior que suministra cargas positivas al dispositivo de Van de Graff y cuyo polo negativo hace el papel de tierra del dispositivo.
• Dos poleas, una inferior dotada de un motor de accionamiento, y una superior con una correa de material aislante ajustada a las dos poleas para transmitir el movimiento de la polea inferior a la superior.
• Un gran cilindro hueco de material aislante que contiene el mencionado sistema mecánico.
• Una gran esfera metálica superior hueca acoplada al cilindro hueco.
• Dos peines metálicos de cerdas muy finas destinados a transmitir las cargas desde el generador inferior hasta la esfera metálica hueca del dispositivo de van de Graaff. El primero está enfrentado a la correa a nivel de la polea inferior y está conectado eléctricamente al polo positivo del generador inferior. El segundo está enfrentado a la correa a nivel de la polea superior. El peine metálico superior está conectado eléctricamente al interior de la esfera metálica hueca.

Funcionamiento del generador de Van de Graff

Generador de Van de Graaff de La Casa Mágica, en el museo St. Louis Children's

• Se pone en marcha el motor que mueve la polea inferior, arrastra en su movimiento a la correa y transmite el movimiento a la polea superior.
• El generador inferior suministra cargas positivas al peine inferior. Con ellas se crea un campo eléctrico elevado en las puntas del peine. Por el poder de las puntas del peine inferior, las cargas positivas son depositadas en la superficie exterior de la polea.
• Las cargas depositadas sobre la correa viajan hasta la polea superior.
• Las cargas positivas que llegan a la altura del peine superior crean un campo eléctrico elevado en las puntas del peine superior. Por el poder de las puntas del peine superior las cargas positivas de la correa son capturadas por el peine y llevadas a la gran esfera metálica.
• Las cargas pasan a la cara externa de la esfera metálica superior.
• El proceso es continuo de forma que en la esfera superior se llega a acumular una enorme cantidad de carga eléctrica positiva. Entre el electrodo de tierra del generador inferior y la esfera metálica superior se crea una diferencia de potencial de varios millones de voltios, lo cual constituye el objetivo del Van de Graff.
• Si se conecta una esfera de prueba a la tierra inferior mediante un cable y se aproxima a la esfera metálica superior, debido a la gran diferencia de potencial existente entre ambas esferas se producirá una gran descarga eléctrica. Como alternativa, en el generador inferior se puede invertir la polaridad, poniendo el electrodo positivo a tierra y el negativo conectado al peine inferior. En estas condiciones las polaridades y las cargas se invierten: la correa arrastra las cargas negativas depositadas por el peine inferior, el peine superior retira las cargas negativas de la correa, la esfera superior adquiere una gran carga negativa y, por tanto, un potencial negativo muy elevado respecto a la tierra.³¹​

Aplicaciones del generador Van de Graaff

La gran diferencia de potencial creada por el generador entre la esfera superior y la tierra inferior se emplea para acelerar partículas cargadas. Las partículas cargadas se producen en una fuente, recorren un tubo acelerador vertical, colocado no lejos de la cinta, e impactan sobre una muestra que hace de blanco. Según se utilice una u otra alternativa se podrán acelerar iones negativos o iones positivos. En resumen, la gran energía potencial electrostática acumulada en el Van de Graaff, de varios millones de electrón-voltios (1 electrón-voltio = 1.610-19 J) se destina a suministrar una gran energía cinética a los iones del acelerador de partículas. El generador de Van de Graaff también se utiliza en Escuelas y Centros de Educación para hacer demostraciones sobre los efectos del alto potencial electrostático alcanzado en su esfera metálica.