CONCEPTOS FÍSICOS

CONCEPTOS TERMODINÁMICOS

 nivel macroscópico es el nivel de descripción en que la posición o estado físico concreto de las partículas que integran un cuerpo puede ser resumido en una ecuación de estado que sólo incluye magnitudes extensivas (volumen, longitud, masa) y magnitudes intensivas promedio (presión, temperatura). Usualmente debido al gran tamaño de dicho sistema pueden despreciarse los efectos cuánticos y puede usarse la física estadística y las leyes de Newton como buena aproximación (en algunos casos si las partículas se mueven muy rápidamente la mecánica relativista). Igualmente la energía total del sistema puede considerarse como una magnitud continua en lugar de como una magnitud cuantizada.

Extendiendo la definición se habla de objeto o fenómeno macroscópico cuando las dimensiones geométricas o la magnitud física sobrepasa de un cierto tamaño. Normalmente todos los objetos visibles a simple vista son a todos los efectos macroscópicos, en oposición a los objetos microscópicos y los fenómenos microscópicos, no visibles a simple vista y donde la mecánica cuántica puede desempeñar un papel importante, en su descripción.

Termodinámica[editar]

La termodinámica se ocupa necesariamente de sistemas macroscópicos, donde la estructura interna del sistema y el comportamiento individual de las partículas no es relevante para las magnitudes termodinámicas. Sólo los agregados del conjunto de partículas cuentan en termodinámica (magnitudes extensivas) o los promedios considerados a partir de un gran número de partículas (magnitudes extensivas). Así por ejemplo la masa o la energía se calcula como suma de las masas o las energías de las partículas que integran el sistema. Mientras que la presión o la temperatura se calculan a partir de la distribución de velocidades (para un gas ideal esta distribución es la distribución de Maxwell-Boltzmann). Para un gas ideal la presión p y la temperatura T se calculan como:

${\displaystyle p={\frac {N}{V}}m_{p}{\bar {v}}_{i}^{2},\quad T={\frac {m_{p}{\bar {v}}_{i}^{2}}{k_{B}}}}$

Donde ${\displaystyle \scriptstyle k_{B}}$ es la constante de Boltzmann. Estas dos ecuaciones conjuntamente implican que se satisface la ecuación de los gases ideales:

${\displaystyle pV=Nk_{B}T}$

Variables macroscópicas[editar]

En un agregado de partículas que mantienen un estado de equilibrio estadístico, cada partícula evoluciona según las reglas de evolución de un cierto sistema dinámico. Sin embargo, el comportamiento global del sistema ignorando las partículas individuales exhibe un comportamiento global que se puede describir estadísticamente. Una variable macroscópica es cualquier variable que se puede definir a partir de una distribución de probabilidadsobre el espacio fásico de microestados que son accesibles a las partículas individuales. Algunos ejemplos típicos de variables macroscópicas son:

• La temperatura.
• La presión de un gas.
• La magnetización de un sólido magnético.
• La energía interna del sistema.

En general para los estados de equilibrio las variables macroscópicas se denominan simplemente funciones de estado.

Potencial de Lennard-Jones para un dímero de argón.

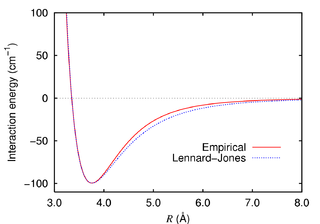
Un par de átomos o moléculas neutros están sujetos a dos fuerzas distintas en el límite de una gran separación y de una pequeña separación: una fuerza atractiva actúa a grandes distancias (fuerza de Van Der Waals, o fuerza de dispersión) y una fuerza repulsiva actuando a pequeñas distancias (el resultado de la sobreposición de los orbitales electrónicos, conocido como la repulsión de Pauli). El potencial de Lennard-Jones (también conocido como el potencial L-J, el potencial 6-12 o, con menor frecuencia, como el potencial 12-6) es un modelo matemático sencillo para representar este comportamiento.

Fue propuesto en 1924 por el matemático y físico teórico inglés John Lennard-Jones (1894-1954).

Formulación[editar]

El potencial de Lennard-Jones es de la forma:

${\displaystyle V(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]}$

donde:

• ${\displaystyle \,\epsilon }$ es la profundidad del potencial,
• ${\displaystyle \,\sigma }$ es la distancia (finita) en la que el potencial entre partículas es cero y
• r es la distancia entre partículas.

Estos parámetros pueden ser ajustados para reproducir datos experimentales o pueden ser deducidos de resultados muy precisos de cálculos de química cuántica. El término ${\displaystyle r^{-12}}$ describe la repulsión y el término ${\displaystyle r^{-6}}$describe la atracción.

La función que describe la fuerza a la que están sujetas las partículas es opuesta al gradiente del potencial arriba descrito:

${\displaystyle {\vec {F}}(r)=-{\vec {\nabla }}V(r)=-{\frac {dV(r)}{dr}}{\hat {r}}=4\epsilon \left(12\,{\frac {{\sigma }^{12}}{{r}^{13}}}-6\,{\frac {{\sigma }^{6}}{{r}^{7}}}\right){\hat {r}}}$

El potencial de Lennard-Jones es una aproximación. La forma del término que describe la repulsión no tiene ninguna justificación teórica; la fuerza repulsiva debe depender exponencialmente de la distancia, pero el término de la fórmula de L-J es más conveniente debido a la facilidad y eficiencia de calcular r¹² como el cuadrado de r⁶. Su origen físico está relacionado al principio de exclusión de Pauli: cuando dos nubes electrónicas circulando los átomos se empiezan a sobreponer, la energía del sistema aumenta abruptamente. El exponente 12 fue elegido exclusivamente por su facilidad de cálculo.

Formas alternativas[editar]

La función del potencial de Lennard-Jones comúnmente se escribe de la siguiente forma:

${\displaystyle V(r)=\epsilon \left[\left({\frac {r_{min}}{r}}\right)^{12}-2\left({\frac {r_{min}}{r}}\right)^{6}\right]}$

donde ${\displaystyle \,r_{min}}$ = ${\displaystyle \,2^{1/6}\sigma }$ es la distancia en la que el potencial se encuentra en un mínimo.

La formulación más sencilla, usada comúnmente por software de simulación, es:

${\displaystyle V(r)={\frac {A}{r^{12}}}-{\frac {B}{r^{6}}}}$

donde:

• ${\displaystyle \,A=4\epsilon \sigma ^{12}\qquad B=4\epsilon \sigma ^{6}\qquad \sigma =\left({\frac {A}{B}}\right)^{\frac {1}{6}}\qquad \epsilon ={\frac {B^{2}}{4A}}}$

Simulación de dinámica molecular: potencial truncado[editar]

En general, para ahorrar tiempo computacional, el potencial de Lennard-Jones es truncado en la distancia límite de ${\displaystyle \displaystyle r_{c}=2.5\sigma }$, donde

${\displaystyle \displaystyle V(r_{c})=V(2.5\sigma )=4\epsilon \left[\left({\frac {\sigma }{2.5\sigma }}\right)^{12}-\left({\frac {\sigma }{2.5\sigma }}\right)^{6}\right]=-0.0163\epsilon =-{\frac {1}{61.3}}\epsilon }$

i.e., en ${\displaystyle \displaystyle r_{c}=2.5\sigma }$, el potencial LJ ${\displaystyle \displaystyle V}$ es aproximadamente 1/60 de su valor mínimo ${\displaystyle \displaystyle \epsilon }$ (profundidad del potencial).

Después de ${\displaystyle \displaystyle r_{c}}$, se le asigna el valor 0 al potencial computacional.

Por otro lado, para evitar una discontinuidad en ${\displaystyle \displaystyle r_{c}}$, como se muestra en la ecuación 1, el potencial de LJ es desplazado ligeramente hacia arriba, de tal forma que el potencial computacional sea 0 exactamente en la distancia límite ${\displaystyle \displaystyle r_{c}}$.

Potencial de Mie[editar]

El potencial de Lennard-Jones es un caso especial del potencial de Mie

${\displaystyle V(r)={\frac {C_{n}}{r^{n}}}-{\frac {C_{m}}{r^{m}}}}$,

ya propuesto en 1903 por el físico alemán Gustav Mie

propiedad residual es un concepto de la termodinámica que se define como la diferencia entre la propiedad de un gas real y la propiedad de un gas ideal, ambos considerados a la misma presión, temperatura y composición.

se denota de la siguiente manera:
${\displaystyle M^{R}=M^{o}-M^{gi}}$

Donde:
M°: cualquier propiedad termodinámica (V, H, S, U) a T y P del sistema.
M^gi: La propiedad en la condición de gas ideal, a T y P del sistema.

 propiedades reducidas de un fluido son un conjunto de variables de estadonormalizadas por las propiedades de estado del fluido en su punto crítico. Estas coordenadas termodinámicas adimensionales, junto con el factor de compresibilidad de una substancia, son la base de la forma más simple del teorema de los estados correspondientes.¹​

Las propiedades reducidas también se utilizan para definir la ecuación de estado de Peng-Robinson, un modelo diseñado para obtener una precisión razonable cerca del punto crítico.²​ También se usan para los exponentes críticos, los cuales describen el comportamiento de propiedades físicas cerca de las transiciones de fase continuas.

Presión reducida[editar]

La presión reducida se define como la presión actual ${\displaystyle p}$ dividida por la presión crítica ${\displaystyle P_{c}}$:¹​

${\displaystyle P_{r}={P \over P_{c}}}$

Temperatura reducida[editar]

La temperatura reducida se define como la temperatura actual dividida por la temperatura crítica:¹​

${\displaystyle T_{r}={T \over T_{c}}}$

Donde las temperaturas actual y crítica se expresan en escalas de temperatura absoluta (Kelvin o Rankine).

Volumen específico reducido[editar]

El volumen específico reducido (o volumen específico pseudoreducido) de un fluido se calcula a partir de la ley de los gases ideales a la temperatura y presión crítica de una substancia:¹​

${\displaystyle v_{r}={\frac {v}{RT_{c}/P_{c}}}\,}$

Esta propiedad es útil cuando se conoce el volumen específico y una de les dos propiedades reducidas (presión o temperatura); en cuyo caso, la tercera propiedad que falta se puede calcular directamente.