CONCEPTOS FÍSICOS

CONCEPTOS FUNDAMENTALES

Detección de ondas gravitacionales

Ir a la navegaciónIr a la búsqueda

Mediciones LIGO de la señal de la onda gravitacional GW150914 realizada por los detectores H1 de Hanford, Washington, EE. UU. (izquierda) y L1 de Livingston, Luisiana, EE. UU. (derecha); y comparación con los 'valores teóricos pronosticados'.

El 11 de febrero de 2016, las colaboraciones LIGO, Virgo y GEO600anunciaron la primera detección de ondas gravitacionales, producidas por la fusión de dos agujeros negros a unos 410 megapársecs de la Tierra.¹​²​³​⁴​ La señal recibió el código GW150914,¹​⁵​ GW es el acrónimo de onda gravitacional (en inglés) y el código numérico representa el año, mes y día de su descubrimiento.

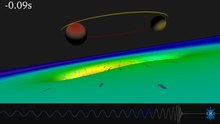
La forma de onda detectada, observada el 14 de septiembre de 2015⁶​ por Marco Drago, un científico del Albert Einstein Institute en Hannover, Alemania,⁷​ es compatible con las predicciones de la relatividad general para la atracción y fusión de un par de agujeros negros y el subsiguiente ringdown del agujero negro final resultante. Las observaciones demostraron la existencia de un sistema binario de agujeros negros de masa estelar y la primera observación de una fusión de un agujero negro binario.

Detectores de LIGO[editar]

Artículos principales: Primera detección de ondas gravitacionales y Lista de observaciones de ondas gravitacionales.

LIGO opera dos observatorios de ondas gravitacionales al unísono: el Observatorio LIGO Livingston (30°33′46.42″N 90°46′27.27″O) en Livingston, Luisiana, y el Observatorio LIGO Hanford, en el DOE Hanford Site (46°27′18.52″N 119°24′27.56″O), localizado cerca de Richland, Washington. Estos sitios están separados por 3,002 kilómetros, es decir, se encuentran a una distancia de 10 milisegundos luz. Las operaciones inicial de LIGO entre 2002 y 2010 no detectaron ninguna onda gravitacional. Este periodo estuvo seguido por un cierre multianual mientras se reemplazaron los detectores por otros mejorados, la versión "Advanced LIGO".⁸​ En febrero 2015, los dos detectores entraron en el modo de ingeniería.⁹​ Fue durante este periodo cuando se detectó el acontecimiento, ya que la fase de operación científica formal no empezó hasta el 18 de septiembre de 2015.

Detección del suceso[editar]

La señal de la onda gravitacional GW150914 fue detectada por los detectores de LIGO en Hanford -H1- (Washington, EE. UU.), y Livingston -L1- (Luisiana, EE. UU.), a las 09:50:45 UTC del 14 de septiembre de 2015. La señal duró unos 0.2 segundos, y aumentó en frecuencia y amplitud en aproximadamente 8 ciclos de 35 a 150 Hz, donde la amplitud alcanzó su máximo. La detección se produjo durante un periodo de tres minutos de adquisición de datos utilizando métodos de búsqueda de baja latencia que proporcionan un análisis inicial rápido de los datos de los detectores. Un análisis estadístico más detallado de la señal y de 16 días de datos (del 12 septiembre a 20 octubre), identificó la GW150914 como un suceso real, con una significación estadística de más de 5.1 sigma.¹​¹⁰​

La señal fue detectada en Livingstone 7 milisegundos antes que en Handford, lo que dada la distancia entre los dos observatorios (están a una distancia de 10 milisegundos luz), es compatible con el hecho de que las ondas gravitacionales se propaguen a la velocidad de la luz.¹​

En el tiempo del acontecimiento, el detector de ondas gravitatorias Virgo estaba inactivo y recibiendo unas mejoras, y GEO600 no fue bastante sensible para detectar la señal.¹​

Según Rainer Weiss, en la primera toma de medidas (entre septiembre de 2015 y enero de 2016) hubo al menos otros cuatro eventos más, más débiles que GW150914.²​

Fusión de agujeros negros[editar]

El análisis de la señal sugirió que fue producida por la fusión de dos agujeros negros con masas de ${\displaystyle 36_{-4}^{+5}}$ veces y 29±4 veces la masa del Sol, resultando en un agujero negro de 62±4 masas solares. Las 3.0±0.5 masas solares restantes corresponden a energía emitida en forma de ondas gravitatorias, según la equivalencia entre masa y energía. El acontecimiento ocurrió a una distancia de ${\displaystyle 410_{-180}^{+160}}$ megapársecs, o 1.3±0.6 miles de millones de años luz.¹​¹¹​ El máximo de potencia emitido superó la potencia luminosa combinada radiada por todas las estrellas en el universo observable.¹⁰​⁴​

Durante los 0,2 segundos de duración de la señal detectable, la velocidad relativa de los agujeros negros aumentó del 30 % al 60 % de la velocidad de la luz, y los objetos que orbitaban a una distancia de unos cuantos centenares de kilómetros antes de fusionarse.¹​¹⁰​

El decaimiento de la forma de onda después del máximo era compatible con la oscilación amortiguada de un agujero negro que relaja a una configuración fusionada final.¹​

Se piensa que el objeto resultante de la fusión es un agujero negro en rotación.¹⁰​

Brazo norte del observatorio de LIGO en Hanford

Anuncio[editar]

El anuncio de la detección se realizó el 11 de febrero de 2016,³​ en una rueda de prensa en Washington D. C. Participaron el director ejecutivo de LIGO, David Reitze, dos de sus creadores, Rainer Weiss y Kip Thorne, la portavoz de la colaboración científica de LIGO, Gabriela González y la directora de la NSF, France A. Córdova.⁴​²​

Había muchos rumores sobre una posible detección con anterioridad al anuncio, empezando poco después del acontecimiento por un tweet de Lawrence Krauss el 25 de septiembre de 2015.¹²​

Implicaciones[editar]

Detecciones futuras[editar]

Se espera que este suceso sea meramente el primero de varias detecciones durante el primer año de operación de los detectores Advanced LIGO. Hay esfuerzos en marcha para mejorar significativamente la red global de detectores de ondas gravitacionales. Estos incluyen la construcción de futuros detectores de Advanced LIGO, con la intención de lograr en su diseño una mayor sensibilidad, lo que permitirá la detección de binaries como GW150914 con relaciones señal-ruido tres veces más alta, cubriendo acontecimientos tres veces más distantes, y aumentando la probabilidad de detecciones de acontecimientos por un factor 27. Además, Advanced Virgo, KAGRA, y un posible tercer LIGO en India extenderán la red y mejorarán significativamente la reconstrucción de posición y estimación de parámetros de las fuentes.¹​ El 27 de agosto de 2017 la Colaboración LIGO-VIRGO hace pública la primera detección desde tres detectores de una onda gravitacional GW170814, siendo la primera detectada por el Advanced Virgo, permitiendo localizar con una gran precisión el origen de la señal gracias a la triangulación de la señal polarizada.

Prueba de la Relatividad General[editar]

La masa y momento angular del agujero negro tras el suceso de fusión son compatibles con las propiedades de los dos agujeros negros antes de la fusión según predice la relatividad general. Esto constituye una prueba de la relatividad general en el régimen de campo fuerte, un régimen que anteriormente era imposible de sondear.¹​

Astrofísica[editar]

El conocimiento de las masas de los dos agujeros negros antes de la fusión proporciona una valiosa información sobre la evolución estelar. Los dos agujeros negros tenían más masa que los agujeros negros estelaresdetectados previamente mediante binarias de rayos X. Esto podría significar que los vientos estelares de las estrellas progenitoras habrían sido relativamente débiles, y que por tanto la metalicidad habría sido menor que la mitad del valor solar.¹³​

El hecho de que los dos agujeros negros estuvieran en un sistema binario impone condiciones a los escenarios de evolución estelar o de formación dinámica (dependiendo de cómo se formara el sistema binario).¹³​

Gravitones[editar]

El gravitón es la hipotética partícula elemental asociada con la gravedad, y teóricamente su masa es nula. Las observaciones de la fase de atracción de los agujeros negros permiten mejorar ligeramente la longitud de onda Compton del gravitón acotándola a ${\displaystyle (\lambda _{g}>10^{13}km)}$ , más de 10 billones de kilómetros, y la cota superior de su masa (${\displaystyle m_{g}<1 .2="" 10="" annotation="" c="" ev="" mathrm="" times="">$).

ecuación de movimiento es la formulación matemática que define la evolución temporal de un sistema físico en el espacio. Esta ecuación relaciona la derivada temporal de una o varias variables que caracterizan el estado físico del sistema, con otras magnitudes físicas que provocan los cambios en este.

En la dinámica del punto material, la ecuación de movimiento determina la posición futura de un objeto o partícula móvil en función de otras variables como, su velocidad, su aceleración, su masa y cuantas variables le puedan afectar en su movimiento junto con las condiciones iniciales. En otras áreas de la física como la mecánica de los medios continuos o la teoría de campos se habla de ecuación de movimiento en general para describir las ecuaciones de evolución o variación temporal del sistema.

Ecuaciones de movimiento en mecánica clásica[editar]

Históricamente el primer ejemplo de ecuación del movimiento que se introdujo en física fue la segunda ley de Newton para sistemas físicos compuestos de agregados partículas materiales puntuales. En estos sistemas el estado dinámico de un sistema quedaba fijado por la posición y velocidad de todas las partículas en un instante dado. Hacia finales del siglo XVIII se introdujo la mecánica analítica o racional, como generalización de las leyes de Newton aplicables a sistemas de referencia inerciales. Se concibieron dos enfoques básicamente equivalentes conocidos como mecánica lagrangiana y mecánica hamiltoniana, que pueden llegar a un elevado grado de abstracción y formalización en ecuaciones diferenciales.

Sistemas discretos[editar]

Artículos principales: Dinámica del punto material y Mecánica del sólido rígido.

Un sistema discreto de partículas o de sólidos rígidos tiene un número finito de grados de libertad. Los ejemplos clásicos de ecuación del movimiento más conocidos son:

1. La segunda ley de Newton que se usa en mecánica newtoniana: ${\displaystyle m{\frac {d^{2}\mathbf {r} }{dt^{2}}}-\mathbf {F} =0}$
2. Las ecuaciones de Euler-Lagrange que aparecen en mecánica lagrangiana: ${\displaystyle {\frac {d}{dt}}\left({\frac {\partial L(q_{i},{\dot {q}}_{i})}{\partial {\dot {q}}_{i}}}\right)-{\frac {\partial L(q_{i},{\dot {q}}_{i})}{\partial q_{i}}}=0}$
3. Las ecuaciones de Hamilton que aparecen en mecánica hamiltoniana: ${\displaystyle {\frac {dq_{i}}{dt}}={\frac {\partial H(p_{i},q_{i})}{\partial p_{i}}}\qquad {\frac {dp_{i}}{dt}}=-{\frac {\partial H(p_{i},q_{i})}{\partial q_{i}}}}$

Sistemas continuos[editar]

Artículos principales: Mecánica de sólidos deformables y Mecánica de fluidos.

Muchos sistemas de la mecánica clásica se modelizan como un medio continuo entre ellos los sólidos deformables y la mecánica de fluidos. Estos sistemas requieren ecuaciones de evolución temporal que involucran ecuaciones diferenciales en derivadas parciales.

Ecuaciones de movimiento en teoría de la relatividad[editar]

En la teoría de la relatividad existen dos tipos de entidades físicas, las partículas y los campos. Aunque en última instancia, tal como establece la teoría cuántica de campos, las partículas son campos materiales altamente localizados, en teoría de la relatividad se pueden tratar las partículas como entes físicos localizados en el espacio-tiempo. La distinción entre estos tipos de entidades físicas hace que en teoría de la relatividad existan dos tipos de ecuaciones de movimiento:

1. Las ecuaciones de movimiento de las partículas materiales, que son la generalización relativista de las ecuaciones de la mecánica clásica.
2. Las ecuaciones de "movimiento" o evolución temporal de los campos físicos.

Ecuaciones de movimiento de partículas[editar]

El análogo de la primera ley de Newton en teoría de la teoría de la relatividad postula que cuando sobre las partículas no actúa ninguna fuerza estas se mueven a lo largo de las geodésicas del espacio-tiempo, es decir, sobre las líneas más "rectas" posibles o de curvatura mínima. Cuando sobre las partículas actúa alguna fuerza, la ecuación del movimiento en términos de tiempo propio de la partícula, los símbolos de Christoffel dependientes de la curvatura del espacio tiempo, y la fuerza total sobre la partícula viene dada por:

${\displaystyle m{\frac {\partial ^{2}x^{k}}{\partial \tau ^{2}}}+m\sum _{i,j=0}^{3}\Gamma _{ij}^{k}{\frac {\partial x^{i}}{\partial \tau }}{\frac {\partial x^{j}}{\partial \tau }}=F^{k}}$

Para una partícula moviéndose a través de un espacio-tiempo plano (${\displaystyle \Gamma _{ij}^{k}=0}$), con velocidad pequeña respecto a la de la luz (${\displaystyle \tau \approx t}$) la anterior ecuación se reduce a la segunda ley de Newton.

Ecuaciones de movimiento en teoría clásica de campos[editar]

Los sistemas físicos formados por un conjunto de partículas interactuantes de la mecánica clásica y los sistemas físicos de partículas relativistas sin interacción, son sistemas con un número finito de grados de libertad, cuyas ecuaciones de movimiento vienen dadas por ecuaciones diferenciales ordinarias como todos los ejemplos anteriores. Sin embargo, los campos físicos además de evolución temporal o variación en el tiempo, presentan variación en el espacio. Esa característica hace que los campos físicos se consideren informalmente como sistemas con un número infinito de grados de libertad. Las peculiaridades de los campos hacen que sus ecuaciones de "movimiento" o evolución temporal vengan dadas por ecuaciones en derivadas parciales en lugar de ecuaciones diferenciales ordinarias.

El campo físico más importante en el contexto de la teoría de la Relatividad Especial es el campo electromagnético, cuyas ecuaciones de evolución temporal vienen dadas por las ecuaciones de Maxwell. Estas ecuaciones pueden escribirse de diversas maneras y de diversas notaciones, aunque en el contexto de la teoría de la relatividad conviene escribirlas en forma explícitamente covariante en términos del tensor campo electromagnético ${\displaystyle F^{\alpha \beta }}$. En esa forma, las ecuaciones se reducen a dos ecuaciones de la forma (unidades cgs):

${\displaystyle {\partial F^{\alpha \beta } \over {\partial x^{\alpha }}}={4\pi \over c}J^{\beta }\qquad {\partial F_{\alpha \beta } \over \partial x^{\gamma }}+{\partial F_{\gamma \alpha } \over \partial x^{\beta }}+{\partial F_{\beta \gamma } \over \partial x^{\alpha }}=\epsilon _{\mu \beta \gamma }g^{\alpha \mu }{\partial F^{\beta \gamma } \over \partial x^{\alpha }}=0}$

Donde se ha usado el convenio de sumación de Einstein, ${\displaystyle J^{\beta }}$ son las componentes del cuadrivector densidad de corriente. En esas ecuaciones aparecen las coordenadas ${\displaystyle (x^{0},x^{1},x^{2},x^{3})=(ct,x,y,z)}$ (donde c es la velocidad de la luz, t el tiempo, y (x,y,z) son las coordenadas cartesianas convencionales del espacio tridimensional. Así la evolución en el tiempo del campo electromagnético, si nos fijamos en un punto concreto del espacio viene medida por las derivadas respecto a la coordenada x0

= ct.

En el contexto de la teoría general de la relatividad aparece un problema adicional. La propia geometría del espacio-tiempo viene representada por un campo tensorial llamado tensor métrico. El propio campo gravitatorio es una manifestación de que la geometría del espacio-tiempo no es plana o euclídea. El campo gravitatorio de hecho es proporcional a la curvatura del espacio-tiempo. Las ecuaciones de evolución vuelven a ser ecuaciones diferenciales en derivadas parciales:

${\displaystyle R_{\alpha \beta }-{g_{\alpha \beta }R \over 2}+\Lambda g_{\alpha \beta }=8\pi {G \over c^{4}}T_{\alpha \beta }}$

${\displaystyle R_{\alpha \beta }={R^{\rho }}_{\alpha \rho \beta }=\partial _{\rho }\Gamma _{\beta \alpha }^{\rho }-\partial _{\beta }\Gamma _{\rho \alpha }^{\rho }+\Gamma _{\rho \lambda }^{\rho }\Gamma _{\beta \alpha }^{\lambda }-\Gamma _{\beta \lambda }^{\rho }\Gamma _{\rho \alpha }^{\lambda }}$

${\displaystyle \Gamma _{\alpha \beta }^{\gamma }={\frac {1}{2}}g^{\gamma \mu }\left({\frac {\partial g_{\mu \alpha }}{\partial x^{\beta }}}+{\frac {\partial g_{\mu \beta }}{\partial x^{\alpha }}}-{\frac {\partial g_{\alpha \beta }}{\partial x^{\mu }}}\right)}$

donde reaparecen los símbolos de Christoffel que aparecían en la ecuación del movimiento de las partículas. A diferencia de las ecuaciones del campo electromagnético, estas ecuaciones del campo gravitatorio o geometría del espacio-tiempo son ecuaciones no lineales debido a la presencia de términos que son el producto de dos Γ. Esto hace que las ecuaciones de Einstein del campo gravitatorio sean de difícil solución.

Ecuaciones de movimiento en mecánica cuántica[editar]

En mecánica cuántica existen diversos tipos de ecuación de movimiento para la función de onda según el tipo de problema o sistema cuántico estudiado. Los ejemplos más conocidos de ecuación del movimiento son:

1. La ecuación de Schrödinger: ${\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+U(\mathbf {r} )\right]\psi (\mathbf {r} ,t)=i\hbar {\frac {\partial \psi (\mathbf {r} ,t)}{\partial t}}}$
2. La ecuación de Klein-Gordon: ${\displaystyle \left[{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-\nabla ^{2}+\mu ^{2}\right]\psi =0}$
3. La ecuación de Dirac: ${\displaystyle i\hbar {\frac {d\psi }{dt}}=\left[c\sum _{i=1}^{3}\alpha _{i}p_{i}+\alpha _{0}mc^{2}\right]\psi }$